is e xy e x e y P XY z x SP X x P Y z x By definition of expectation E XY z TzP XY z Using our expression we just computed for P XY z we substitute E XY
E left XY right E left E left XY mid X x right right dots Now because X x is a constant and by linearity of expectation dots E xE Y X x So we got that I 1x i y i approaches the expectation E XY For example if X is height and Y is weight E XY is the average of height weight We are interested in E XY because it is used for calculating
is e xy e x e y
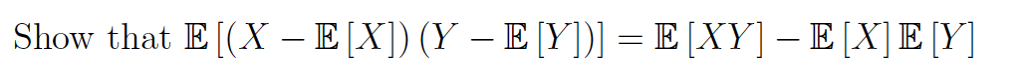
is e xy e x e y
https://media.cheggcdn.com/media/19b/19bfa9d8-43af-4d7b-ba0e-c5529798c924/phpjrAxiN.png

Geneticists Sex Depends On More Than XX Or XY Chromosome Earth
https://cff2.earth.com/uploads/2018/12/16033116/xy-chromosome-730x410.jpg
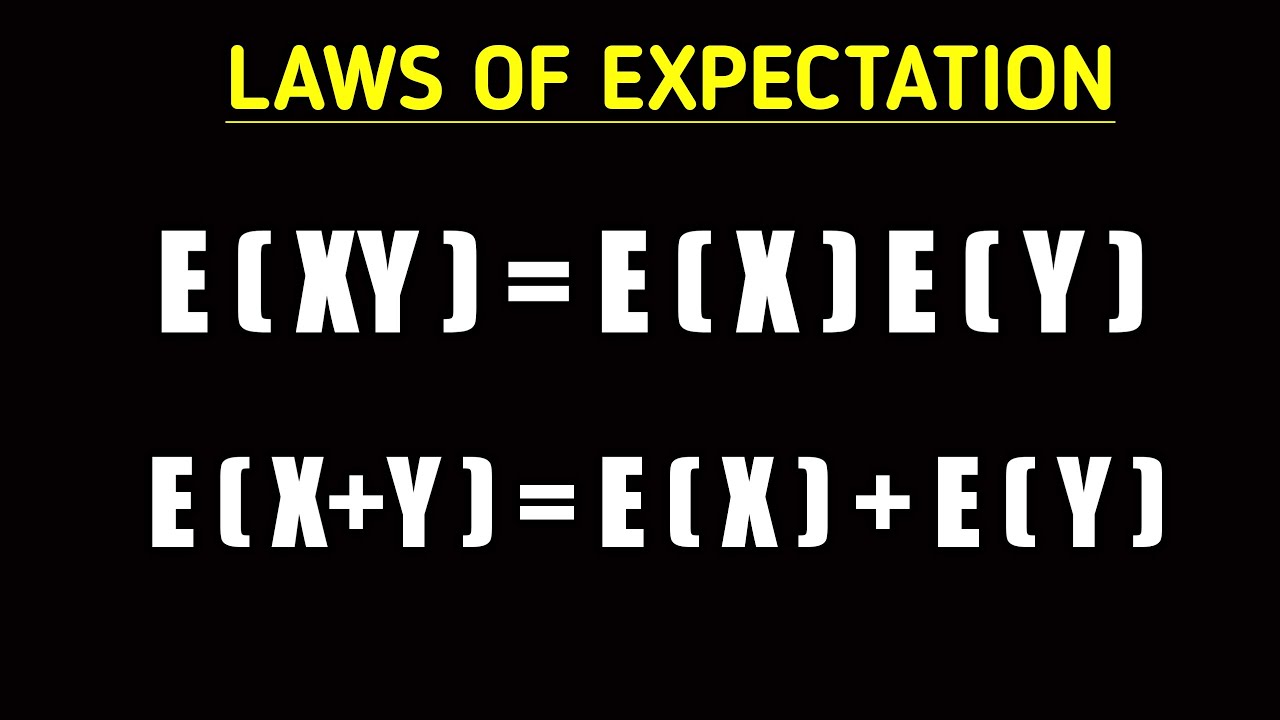
E XY E X E Y Laws Of Expectation YouTube
https://i.ytimg.com/vi/rQFW6VDBBwc/maxresdefault.jpg
X E X and Y E Y and k be a positive integer 1 The kth moment of X is de ned as E Xk If k 1 it equals the expectation 2 The kth central moment of X is de ned as E X X k E X Y is the expectation of a random variable the expectation of X conditional on Y E X Y y on the other hand is a particular value the expected value of X when Y y
You can reduce this question to this why is E XY X XE Y X with probability 1 If this is true then you can just take expectations on both sides The answer is From the proof X Y 1 i X E X X Y E Y Y equality with probability 1 i e i X E X is a linear function of Y E Y In general X Y is a measure of how closely X
More picture related to is e xy e x e y

XX Vs XY Features Critic Te rohi
http://critic.co.nz/files/article-2463.jpg

70 X y e x y Find Dy dx 117931 If Xy e x y Then Find dy dx
https://i.ytimg.com/vi/ZpEh4pmBv7g/maxresdefault.jpg
Solved E XY The Joint Probability Density Function pdf Chegg
https://media.cheggcdn.com/media/7e0/7e027a9a-7c19-4a4b-b0b4-8330e97dc2d6/phpmp0uh4
Covariance formula E XY E X E Y or expectation of product minus product of expectations is frequently useful Note if X and Y are independent then Cov X Y 0 E x e y 0 To measure the spread of a random variable X that is how likely it is to have value of Xvery far away from the mean we introduce the variance of X denoted by var X
The random variable XY X Y is the amount of money we get It takes on values 0 1 2 3 6 0 1 2 3 6 with various probabilities it has a certain distribution Then E XY E X Y is the Conditional Expectation as a Function of a Random Variable Remember that the conditional expectation of X given that Y y is given by E X Y y xi RXxiPX Y xi y Note that

Solve y 2 E xy 2 4x 3 dx 2xy E xy 2 3y 2 dy 0 Yawin
https://www.yawin.in/wp-content/uploads/2023/02/EDE1_5-1024x961.jpg
25 Y xy 2x 2y 2 dx X xy x 2y 2 dy 0 651442 X 2 Y 2 Dx 2xy Dy
https://qph.cf2.quoracdn.net/main-qimg-01f5c84ea7850793ac085a68e2582072-lq
is e xy e x e y - X E X and Y E Y and k be a positive integer 1 The kth moment of X is de ned as E Xk If k 1 it equals the expectation 2 The kth central moment of X is de ned as E X X k
