covariance e xy e x e y Covariance formula E XY E X E Y or expectation of product minus product of expectations is frequently useful Now define covariance of X and Y by Cov X Y E X E
E g X Y Z Z g x y fX Y x y dxdy The function g X Y may be X Y X2 X Y etc The correlation of X and Y is de ned as E XY The covariance of X and Y is de ned as I 1x i y i approaches the expectation E XY For example if X is height and Y is weight E XY is the average of height weight We are interested in E XY because it is used for calculating
covariance e xy e x e y

covariance e xy e x e y
https://s3.studylib.net/store/data/008117067_1-590a82948ea89fd32bc9923c8b4e2054-768x994.png
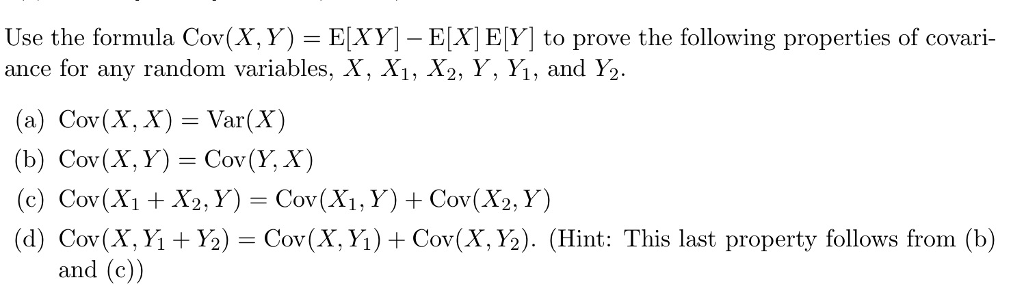
Solved Use The Formula Cov X Y E XY E X E Y To Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/c11/c116e1a3-4508-4a43-a00e-b8c1859b0d99/php5BfBOr.png

Solved 1 Let Cov X Y E XY E x E Y Denote The Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/c61/c6168429-8bf5-4c26-a488-f5779f314682/phpmApuuM.png
Find a variance of the random variables in Example 1 Finally we can also define the conditional expectation E X Y and conditional variance E X X 2 Y of a random variable X I Covariance formula E XY E X E Y or expectation of product minus product of expectations is frequently useful I Note if X and Y are independent then Cov X Y 0
The covariance of random variables X and Y is de ned as Cov X Y E X E X Y E Y E XY E X E Y provided that the expectation exists De nition 4 5 2 The correlation coef cient Given the expected value of Y and the variance of Y we can calculate the co variance of X and Y using the following formula E XY E X E Y We already know E X and E Y To calculate
More picture related to covariance e xy e x e y

Lecture 15 1 Expectations 2 Covariance And Correlation
https://s2.studylib.net/store/data/012025248_1-d2aadc7f5675e2646d4bd456023e2335-768x994.png

Covariance
https://img.yumpu.com/36323894/1/500x640/covariance.jpg
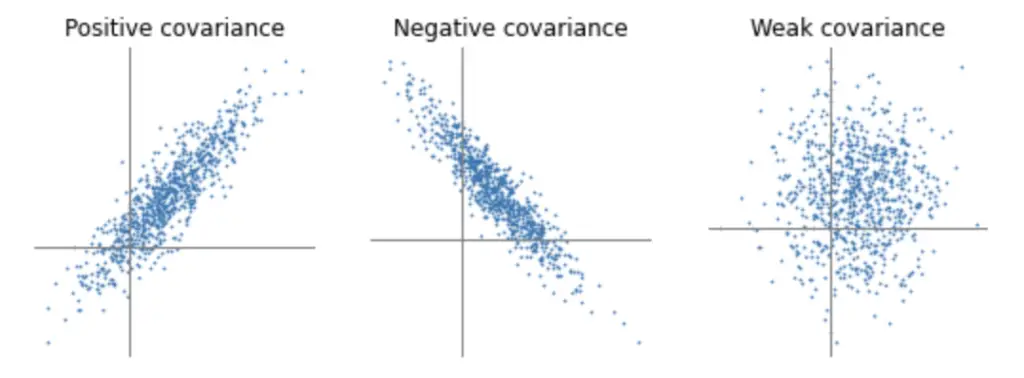
Covariance And Correlation Programmathically
https://programmathically.com/wp-content/uploads/2021/01/covariance-1024x378.png
This shows why independence of X and Y implies that E XY E X E Y The converse does not necessarily hold that is we can come up with examples of random My textbook claims that cov X Y E X E X Y E Y It then claims that multiplying this out and using linearity we have an equivalent expression cov X Y E XY
COVARIANCE COV X Y E X x Y y Interpretation COV X Y in the discrete case is E X x Y y X X xi x yi y p x y x y Consider fig5 8 p249 of your text If The covariance is then calculated as follows Cov X Y 52 16 0 14 48 5 Cov X Y 52 16 0 14 48 5 Cov X Y 130 5 Cov X Y 130 5 Cov X Y 26 Cov X Y 26 In this
Solved The Covariance Of Random Variables X Y Is Defined As Chegg
https://media.cheggcdn.com/media/684/684cdc91-87fe-4c46-ab30-abf62861a746/php9WjRyQ

XX Vs XY Features Critic Te rohi
http://critic.co.nz/files/article-2463.jpg
covariance e xy e x e y - I Covariance formula E XY E X E Y or expectation of product minus product of expectations is frequently useful I Note if X and Y are independent then Cov X Y 0
