e xy e x e y proof

e xy e x e y proof This shows why independence of X and Y implies that E XY E X E Y The converse does not necessarily hold that is we can come up with examples of random

I 1x i y i approaches the expectation E XY For example if X is height and Y is weight E XY is the average of height weight We are interested in E XY because it is used for calculating Basically E XY E E XY Y E YE X Y The first step is the iterated rule of conditional expectation For the second use the fact that given Y Y is like a constant

e xy e x e y proof

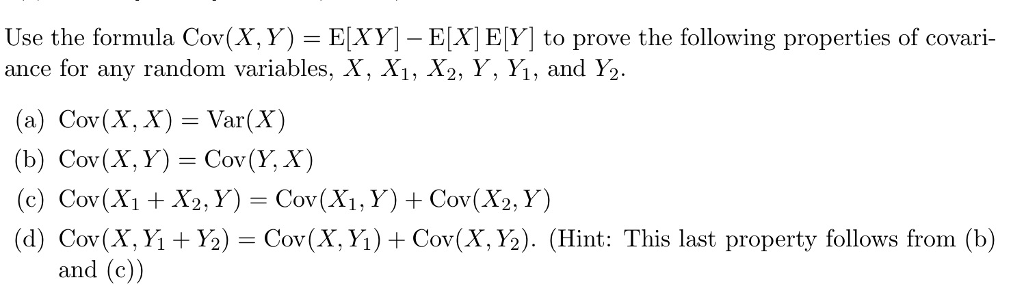
e xy e x e y proof
https://d2vlcm61l7u1fs.cloudfront.net/media/c11/c116e1a3-4508-4a43-a00e-b8c1859b0d99/php5BfBOr.png

Probability Theory Proving That E E X Y EX Mathematics Stack
https://i.stack.imgur.com/HAWKI.png

Solved Definition The Covariance Between X And Y Is Cor X Chegg
https://media.cheggcdn.com/media/f73/f7391f6e-7ac0-4b5d-99d7-e340ace316d2/phpfYkIQp.png

X E X and Y E Y and k be a positive integer 1 The kth moment of X is de ned as E Xk If k 1 it equals the expectation 2 The kth central moment of X is de ned as E X X k From the proof X Y 1 i X E X X Y E Y Y equality with probability 1 i e i X E X is a linear function of Y E Y In general X Y is a measure of how closely X

The equation e xy e x e y holds true and can be proven by utilizing the properties of exponential functions To prove the equation e xy e x e y we start with the Here s the proof Cov X Y E X X Y Y E XY XY X Y X Y E XY XE Y E X Y X Y E XY X Y Covariance can be positive zero or negative Positive indicates that there s an

More picture related to e xy e x e y proof

Solved Let X And Y Be Random Variables With Mu X E X Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/6e6/6e685980-79af-4933-9b81-b4feb2dc79e3/phpJPe8o5.png

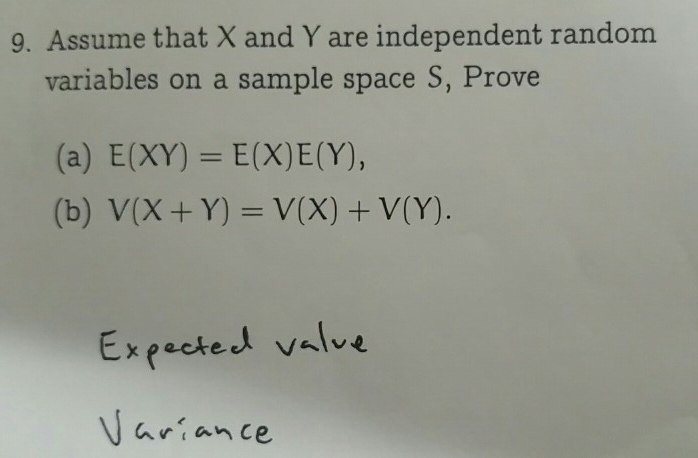
Solved 9 Assume That X And Y Are Independent Random Chegg
https://media.cheggcdn.com/media/533/533451cc-ba60-45ae-b819-ae50ab150b09/image.png

E x E y E x Y Dy dx E y X
https://d10lpgp6xz60nq.cloudfront.net/ss/web-overlay-thumb/13604125.webp

Let X colon Omega to mathbb R k and Y colon Omega to mathbb R k be random variables in some probability space Omega mathcal F mathbb P and let alpha 1 If X and Y are independent r v s then E XjY E X Proof As we know X and Y are independent if and only if fX Y x y fX x fY y or equiva lently fXjY xjy fX x But then

Let X and Y be the random variables that equal to the result of the rst and second die respectively As p X i Y j 1 36 for any i j 2f1 2 3 4 5 6g and p X i 1 6 p Y j Why is E XY E XE Y X Is this using the properties of conditional expectation and is there a general formula that can be applied when you have E E E Y X

Qu Es La Hemicigosis Curiosoando
https://curiosoando.com/wp-content/uploads/2017/09/cromosomas-XY-3D.jpg

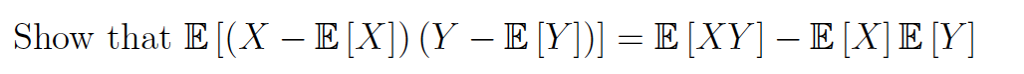
Solved Show That E X E X y E Y E Xy E X E y Chegg
https://media.cheggcdn.com/media/19b/19bfa9d8-43af-4d7b-ba0e-c5529798c924/phpjrAxiN.png

e xy e x e y proof - My textbook claims that cov X Y E X E X Y E Y It then claims that multiplying this out and using linearity we have an equivalent expression cov X Y E XY