e xy example XY denotes a new random variable You could call it Z if you want and work out its distribution Then E XY just means E Z
I approaches the expectation E XY For example if X is height and Y is weight E XY is the average of height weight We are interested in E XY because it is used for calculating the If X and Y are 2 dependent variables how does their combined expectation look For example if flipping a fair coin n times with X representing the number of heads and Y
e xy example

e xy example
https://img.audiofanzine.com/images/u/product/normal/pioneer-xy-101-221452.jpg

J Xy
https://s2.studylib.net/store/data/010538090_1-8c7cbcf45238750975d0dc78dd6af9db-768x994.png
XfXDbWb6y6IHysth kkf62aLri4Kn9LkuqJbSAVqCt xoBCFJh35Npx
https://yt3.googleusercontent.com/XfXDbWb6y6IHysth-kkf62aLri4Kn9LkuqJbSAVqCt-xoBCFJh35Npx_VVxxmNNzt5niXwDn0Q=s900-c-k-c0x00ffffff-no-rj
Theorem 1 Expectation Let X and Y be random variables with finite expectations If g x h x for all x R then E g X E h X Let s use these definitions and rules to calculate the Suppose X and Y are independent each having a uniform distribution on 0 1 Then for example E XY xydxdy ydy E X E Y This is in fact true in general for independent
Multiplication E XY E X E Y if X and Y are independent Another common property of random variables we are interested in is the Variance which measures the squared deviation Covariance formula E XY E X E Y or expectation of product minus product of expectations is frequently useful Note if X and Y are independent then Cov X Y 0
More picture related to e xy example

XY Labs
https://xylabs.com/img/share1.jpg

xy Sequence
https://i.pinimg.com/originals/f6/19/dd/f619dde2fc549f9c94c49ba3692bcc36.jpg

Xy Logo
https://logodix.com/logo/2094692.jpg
Consider E XY Again we have the formula of the same type E XY int Omega X omega Y omega rm d P omega Finally we want to obtain E x e y 0 To measure the spread of a random variable X that is how likely it is to have value of Xvery far away from the mean we introduce the variance of X denoted by var X
In Probability 1 you showed that E aX bY c aE X bE Y c and Var aX bY c a2Var X b2Var Y 2abCov X Y it is simple to obtain a similar result for the covariance of You can reduce this question to this why is E XY X XE Y X with probability 1 If this is true then you can just take expectations on both sides The answer is
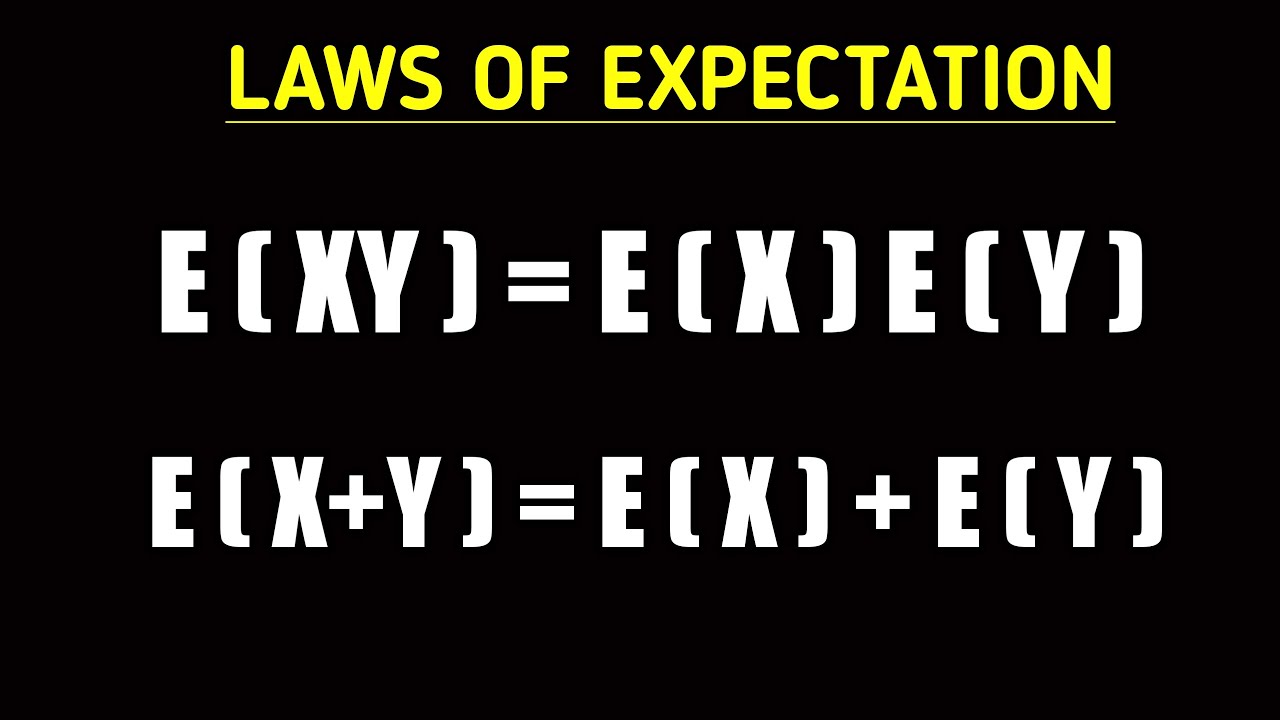
E XY E X E Y Laws Of Expectation YouTube
https://i.ytimg.com/vi/rQFW6VDBBwc/maxresdefault.jpg
![]()
Solved Expected Value Of XY 9to5Science
https://sgp1.digitaloceanspaces.com/ffh-space-01/9to5science/uploads/post/avatar/117163/template_expected-value-of-xy20220526-4060948-7wmgxg.jpg
e xy example - Suppose X and Y are independent each having a uniform distribution on 0 1 Then for example E XY xydxdy ydy E X E Y This is in fact true in general for independent