cov x y e xy e x e y proof Here s the proof Cov X Y E X X Y Y E XY XY X Y X Y E XY XE Y E X Y X Y E XY X Y Covariance can be positive zero or negative Positive indicates that there s an
My textbook claims that cov X Y E X E X Y E Y It then claims that multiplying this out and using linearity we have an equivalent expression cov X Y E XY begingroup First observe that it suffices to prove Cov X Y Cov X E Y X for X Y with E X E Y 0 Now can you prove this endgroup
cov x y e xy e x e y proof

cov x y e xy e x e y proof
https://s2.studylib.net/store/data/012025248_1-d2aadc7f5675e2646d4bd456023e2335-768x994.png

Solved 3 We Know That Cov X Y E X E X Y E Y Use Chegg
https://media.cheggcdn.com/media/eb0/eb0ef555-6552-42db-9aa6-5d72034af31f/php6eou71.png

Ques 12 MCQ If E x E y E x y Then Is Teachoo
https://d1avenlh0i1xmr.cloudfront.net/bbce4bac-05a4-4441-8e54-db75799ec025/slide31.jpg
Rewrite as Cov X Y E Y X 0 which is true because E Y X of Y is an orthogonal projection onto space of functions measurable with respect to sigma X This theorem gives us a method for computing COV X Y COV X Y E XY x y It is easy to prove Read it p251 If X and Y are independent then E XY E X E Y x y Make sure
To show this set g X X E X and h Y Y E Y then Cov X Y E X E X Y E Y E X E X E Y E Y 0 However if X and Y are uncorrelated they are not necessarily Cov X Y E X E X Y E Y E XY E X E Y this is a generalization of variance to two random variables and generally measures the degree to which X and Y tend to be large or
More picture related to cov x y e xy e x e y proof
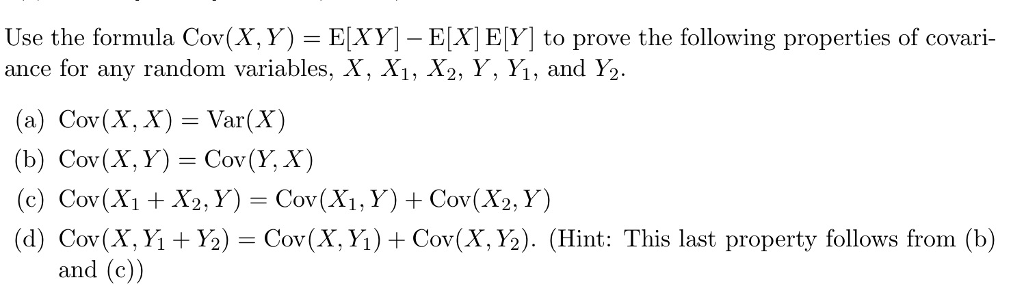
Solved Use The Formula Cov X Y E XY E X E Y To Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/c11/c116e1a3-4508-4a43-a00e-b8c1859b0d99/php5BfBOr.png

Solved 1 Let Cov X Y E XY E x E Y Denote The Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/c61/c6168429-8bf5-4c26-a488-f5779f314682/phpmApuuM.png

Independent Random Variables Proof E g x H y I J Yhxg Ii
https://d20ohkaloyme4g.cloudfront.net/img/document_thumbnails/7e48dac9390a8e08026fd65efaaa9046/thumb_1200_1553.png
So cov X Y E XY E X E Y equals 0 only if E XY P X 1 Y 1 equals p1p2 P X 1 P Y 1 showing that X 1 and Y 1 are independent events It is a Cov X Y E XY EX EY Note If X Y are independent then E XY EX E Y Therefore cov X Y 0 Let W X Y Zrandom variables and a b c dconstants Find cov a X Y cov a
For such random variables the covariance cov X Y of X and Y is defined as cov X Y E X X Y Y where the expectation shown exists and has finite value because of our I read from my textbook that text cov X Y 0 does not guarantee X and Y are independent But if they are independent their covariance must be 0 I could not think of any proper
SOLVED Let X Y Be Random Variables And C B Are Real Numbers Derive
https://cdn.numerade.com/ask_previews/216f947e-3c66-4885-a6eb-551e1d36c09f_large.jpg
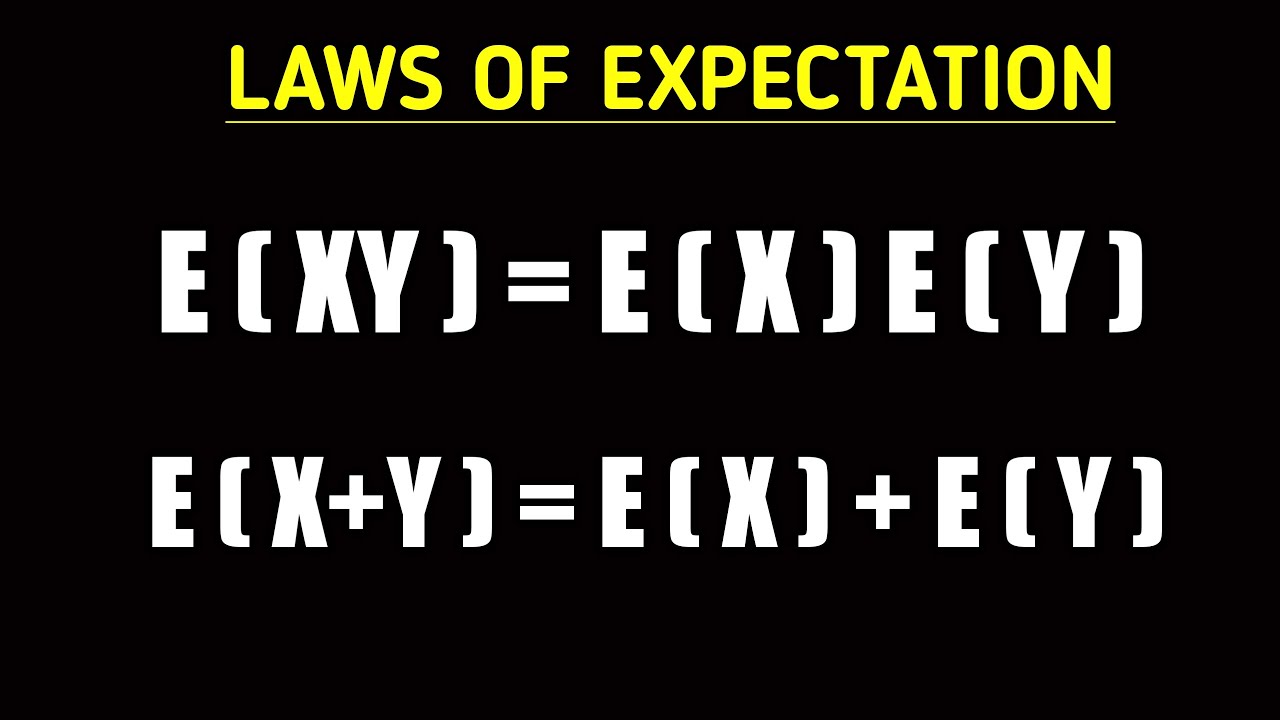
E XY E X E Y Laws Of Expectation YouTube
https://i.ytimg.com/vi/rQFW6VDBBwc/maxresdefault.jpg
cov x y e xy e x e y proof - The proof is the following The i j entry of E X YT E X E Y T is E Xi Yj E Xi E Yj which by the standard computational formula is Cov Xi Yj which in turn is the i