logarithm A logarithm is defined as the power to which a number must be raised to get some other values It is the most convenient way to express large numbers A logarithm has various important properties that prove multiplication and division of logarithms can also be written in the form of logarithm of addition and subtraction
Common Logarithms Base 10 Sometimes a logarithm is written without a base like this log 100 This usually means that the base is really 10 It is called a common logarithm Engineers love to use it On a calculator it is the log button Logarithm the exponent or power to which a base must be raised to yield a given number Expressed mathematically x is the logarithm of n to the base b if bx n in which case one writes x log b n For example 2 3 8 therefore 3 is the logarithm of 8 to base 2 or 3 log 2 8 In the same fashion since 10 2 100 then 2 log 10 100
logarithm
logarithm
https://imgv2-2-f.scribdassets.com/img/document/451343007/original/6ae4a12fb0/1607714239?v=1

Logarithm Rules Study Pivot 2 Medium
https://cdn-images-1.medium.com/max/1600/1*AvjkLYUMrXaJNNMAmlotiw.png

Exercise 3BLogarithms And Laws Of Logarithms Mathematics Tutorial
http://doylemaths.weebly.com/uploads/4/7/0/6/47063657/9526175_orig.png
You will learn what logarithms are and evaluate some basic logarithms This will prepare you for future work with logarithm expressions and functions Solving Exponential Equations Logarithms provide a way to solve equations involving exponents When you have an equation of the form a x b taking the logarithm of both sides allows you to solve for x This is particularly useful when dealing with exponential growth or decay problems
A logarithm is defined using an exponent b x a log b a x Here log stands for logarithm The right side part of the arrow is read to be Logarithm of a to the base b is equal to x A very simple way to remember this is base stays as the base in both forms and base doesn t stay with the exponent in log form A logarithm is the inverse of the exponential function Specifically a logarithm is the power to which a number the base must be raised to produce a given number For example log 2 64 6 because 2 6 64 In general we have the following definition z is the base x logarithm of y if and only if x z y In
More picture related to logarithm
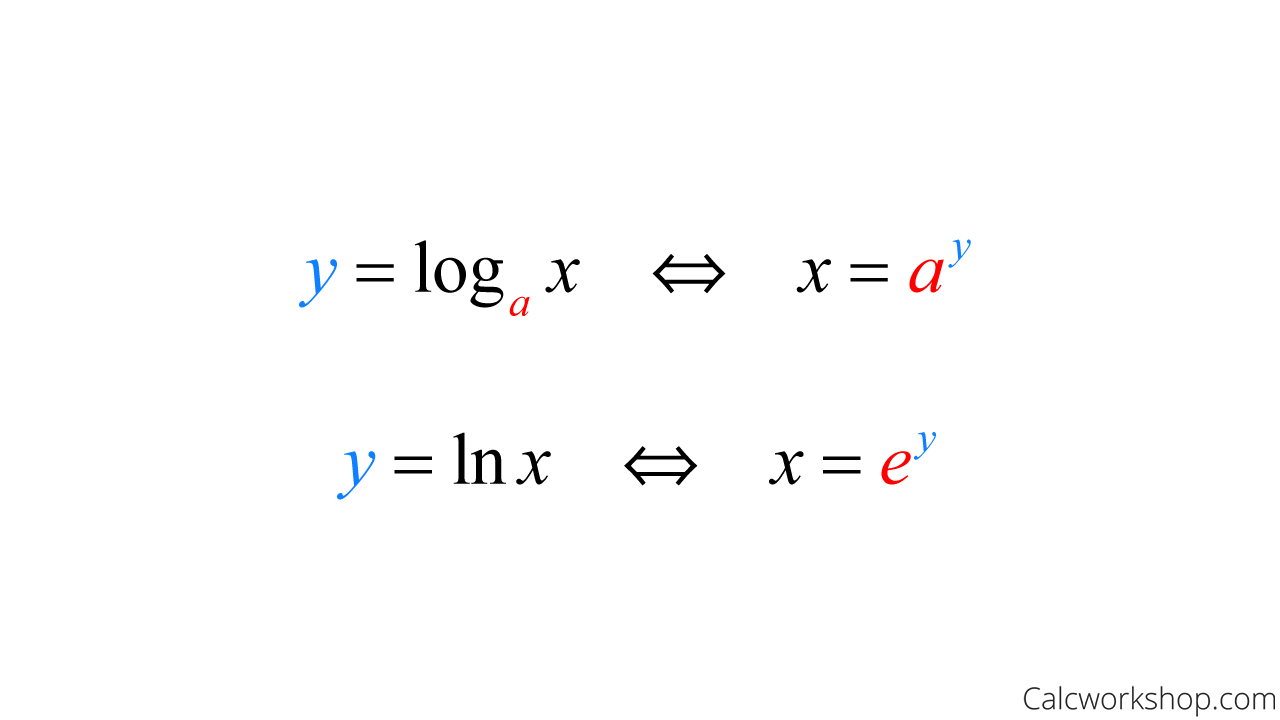
Logarithm Formula
https://calcworkshop.com/wp-content/uploads/log-equation.png

Chapter 06 Exponential And Logarithmic Functions Core Vocabulary
http://upload.wikimedia.org/wikipedia/commons/thumb/1/17/Binary_logarithm_plot_with_ticks.svg/2000px-Binary_logarithm_plot_with_ticks.svg.png

Logaritmus Logarithm Abcdef wiki
https://upload.wikimedia.org/wikipedia/commons/8/81/Logarithm_plots.png
About this unit Logarithms are the inverses of exponents They allow us to solve challenging exponential equations and they are a good excuse to dive deeper into the relationship between a function and its inverse Key Takeaways Given any base b 0 and b 1 we can say that logb1 0 logbb 1 log1 bb 1 and that logb 1 b 1 The inverse properties of the logarithm are logbbx x and blogbx x where x 0 The product property of the logarithm allows us to write a product as a sum logb xy logbx logby
[desc-10] [desc-11]
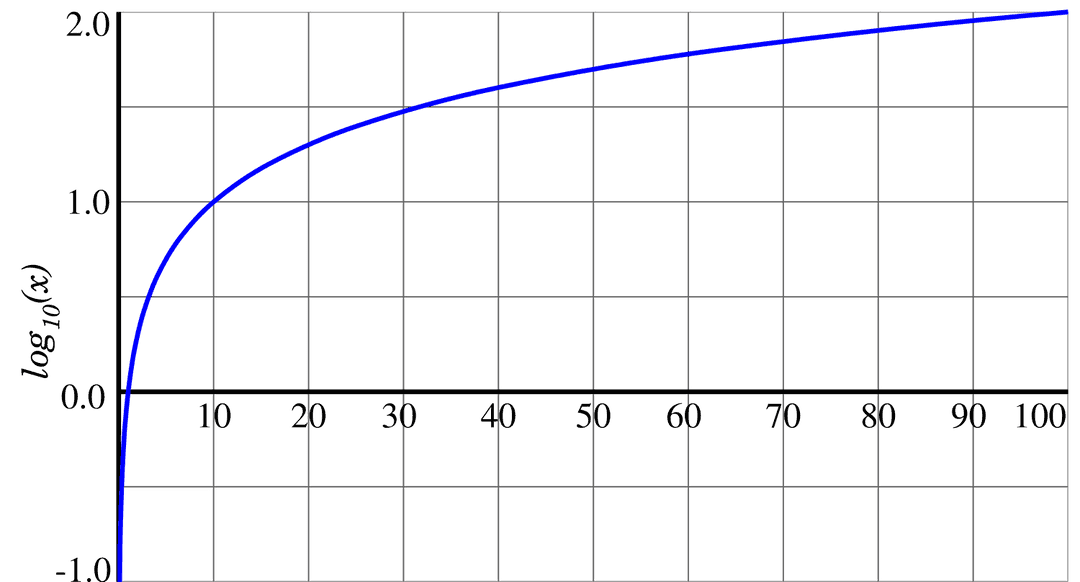
Common logarithm Wikiwand
https://wikiwandv2-19431.kxcdn.com/_next/image?url=https:%2F%2Fupload.wikimedia.org%2Fwikipedia%2Fcommons%2Fthumb%2F7%2F7f%2FGraph_of_common_logarithm.svg%2F1500px-Graph_of_common_logarithm.svg.png&w=1080&q=50

Logarithm Formula
http://formulainmaths.in/wp-content/uploads/2023/04/log-page-001-1.jpg
logarithm - You will learn what logarithms are and evaluate some basic logarithms This will prepare you for future work with logarithm expressions and functions
