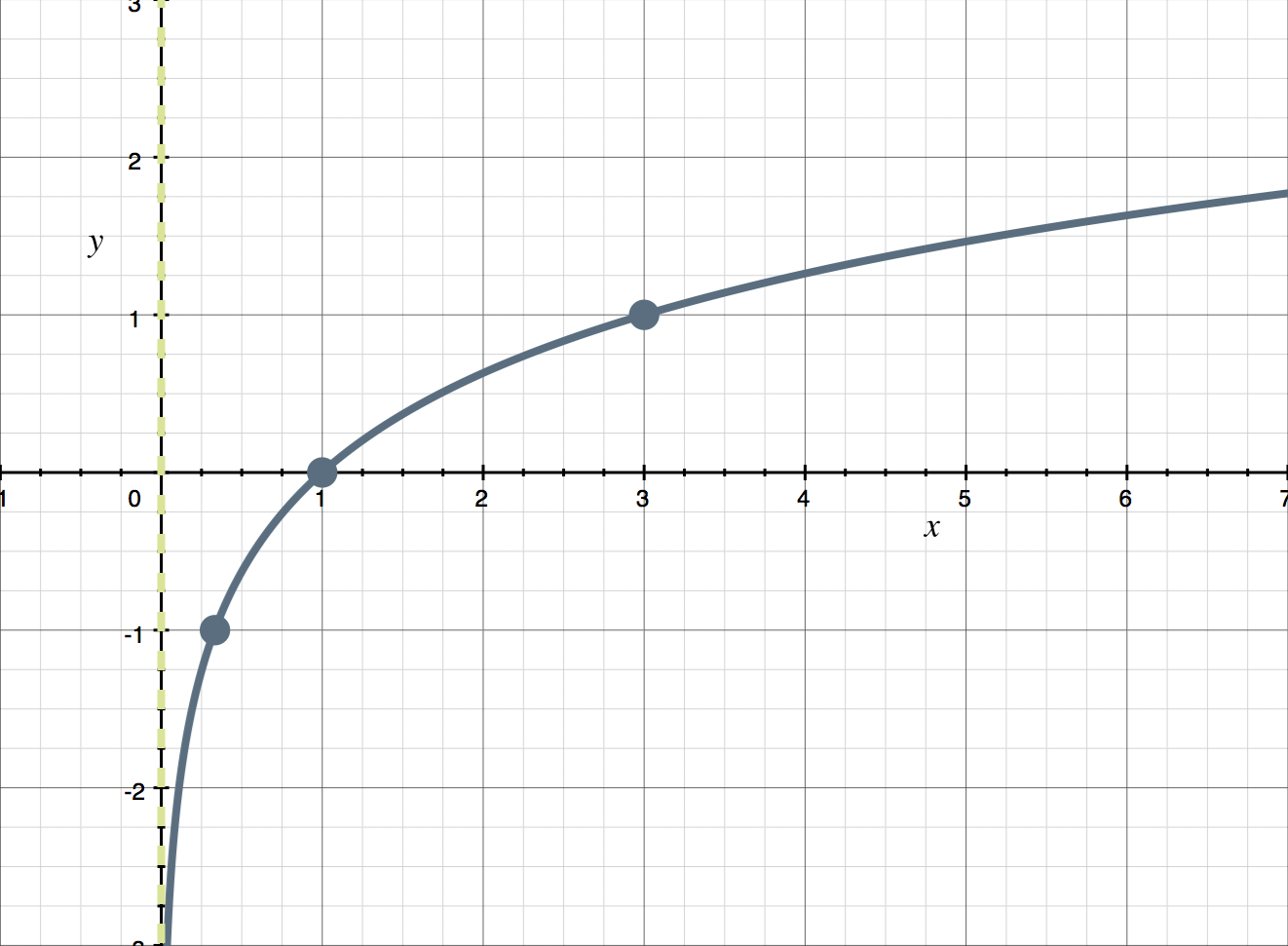
logarithmic The exponent says how many times to use the number in a multiplication In this example 23 2 2 2 8 2 is used 3 times in a multiplication to get 8 So a logarithm answers a question like this In this way The logarithm tells us what the exponent is In that example the base is 2 and the exponent is 3 So the logarithm answers
Learn about the properties of logarithms that help us rewrite logarithmic expressions and about the change of base rule that allows us to evaluate any logarithm we want using the calculator Logarithm the exponent or power to which a base must be raised to yield a given number Expressed mathematically x is the logarithm of n to the base b if bx n in which case one writes x log b n For example 2 3 8 therefore 3 is the logarithm of 8 to base 2 or 3 log 2 8 In the same fashion since 10 2 100 then 2 log 10 100
logarithmic

logarithmic
https://upload.wikimedia.org/wikipedia/commons/8/81/Logarithm_plots.png
Logarithmic Scale Energy Education
https://energyeducation.ca/wiki/images/9/9c/LogLinScale.png

Calculus Help The Natural Logarithm Integrals Involving The Natural
http://1.bp.blogspot.com/_FS5ruccwuL8/TS35kxZahII/AAAAAAAAAEc/ry38oYkbrO8/s1600/Log+Ex+2.jpg
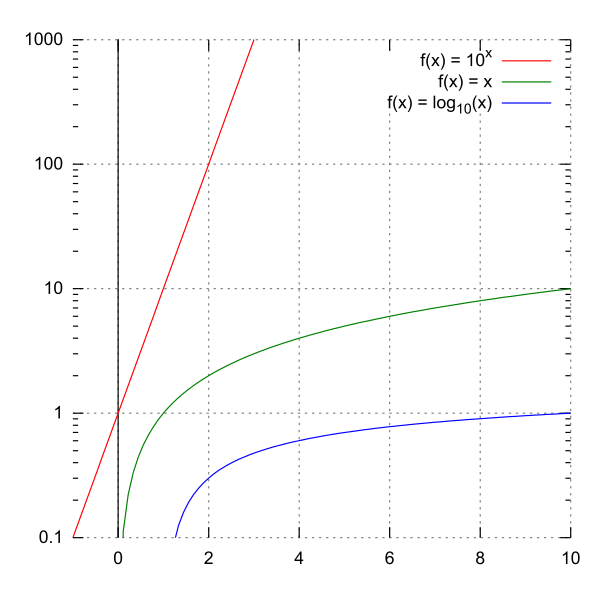
A logarithmic scale or log scale is a method used to display numerical data that spans a broad range of values especially when there are significant differences between the magnitudes of the numbers involved Multiplication and division of numbers can be converted to addition and subtraction respectively using logarithmic properties Measuring Relative Magnitudes Logarithms allow us to express large ranges of numbers in a more manageable form
Specifically a logarithm is the power to which a number the base must be raised to produce a given number For example log 2 64 6 because 2 6 64 In general we have the following definition z is the base x logarithm of y if and only if x z y In typical notation Intro to logarithm properties Learn about the properties of logarithms and how to use them to rewrite logarithmic expressions For example expand log 3a These properties apply for any values of M N and b for which each logarithm is defined which is M
More picture related to logarithmic

Asymptotes Of Logarithmic Graphs Expii
https://d20khd7ddkh5ls.cloudfront.net/img08_72.jpg
How To Draw Logarithmic Graphs Behalfessay9
https://images.squarespace-cdn.com/content/v1/533db07de4b0d9f7ba7f1e77/1610979235221-IIERRRC2I56HINEEX2PK/vertical+asymptote+of+a+logarithmic+function
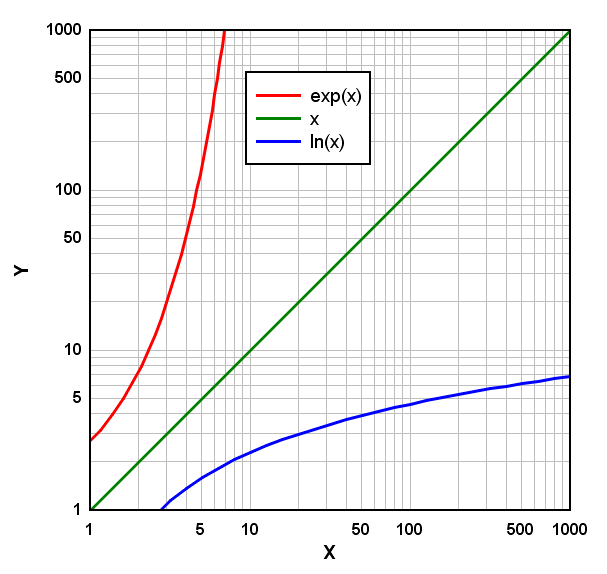
DPlot Logarithmic Scale
http://www.dplot.com/logarithmic/loglog_h600.png
Logarithms In Mathematics logarithms are the other way of writing the exponents A logarithm of a number with a base is equal to another number A logarithm is just the opposite function of exponentiation For example if 102 100 then log10 100 2 Key Takeaways Given any base b 0 and b 1 we can say that logb1 0 logbb 1 log1 bb 1 and that logb 1 b 1 The inverse properties of the logarithm are logbbx x and blogbx x where x 0 The product property of the logarithm allows us to write a product as a sum logb xy logbx logby
[desc-10] [desc-11]
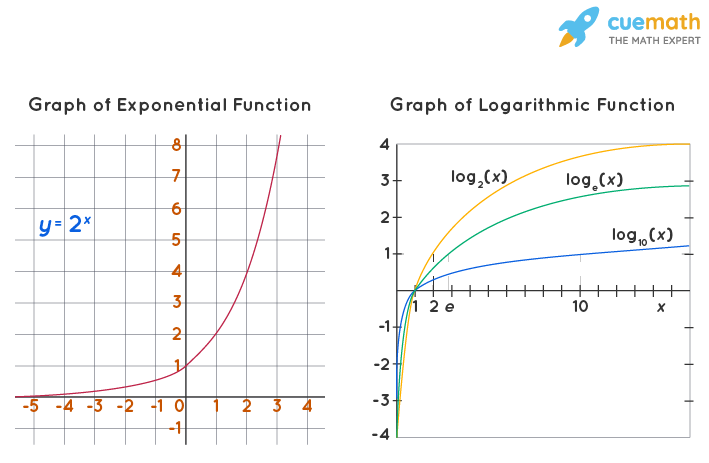
Logarithmic Functions Formula Domain Range Graph
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/logarithmic-function2-1621936133.png
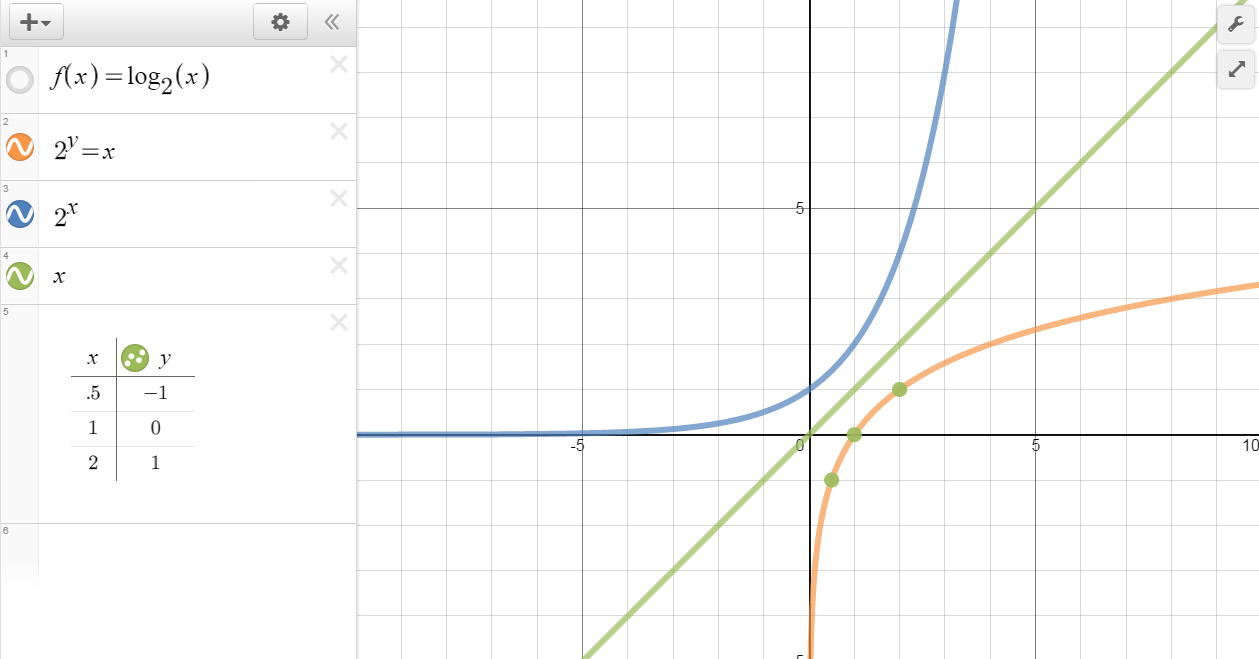
Logarithmic Functions Systry
http://systry.com/wp-content/uploads/2014/09/GraphLogBase2ofx.png
logarithmic - [desc-14]