x y 3 expansion 1 Answer Consider Pascal s Triangle as shown in the following diagram The expansion of the above binomial will have n 1 terms in A B n So our binomial expansion will have 10 1 11 terms We now search for the row in the triangle with 11 terms This is the bottom most row with coefficients 1 10 45 45 10 1
The expansion is y 5 5y 4x 10y 3x 2 10y 4x 3 5y 5x 4 x 5 We need to use Pascal s Triangle shown in the picture below for this expansion Because the binomial is raised to the 5th power we need to use the 5th row of the triangle The 5th row is the one that features color red 1 5 10 10 5 and color red 1 A 3 3a 2b 3ab 2 b 3 Use the Binomial expansion note the exponents sum to the power in each term x y 3 3C 0x 3y 0 3C 1x 2y 1 3C 2x 1y 2 3C 3x 0y 3
x y 3 expansion

x y 3 expansion
https://i.ytimg.com/vi/cSHsNvpowQQ/maxresdefault.jpg

X Y
https://s2.studylib.net/store/data/009827830_1-f9adfb2c4733463eced78b7b95b0525b-768x994.png
x y 3 Expand Formula 597651 How To Expand x y 3
https://concept-stories.s3.ap-south-1.amazonaws.com/test/Stories - Images_story_26368/image_2019-11-07 08:49:36.385305%2B00:00
x y 6 x 6 6x 5y 15x 4y 2 20x 3y 3 15x 2y 4 6xy 5 y 6 Explanation The Binomial Theorem gives a time efficient way to expand binomials raised to a power and may be stated as Explanation The binomial theorem tells us that if we have a binomial a b raised to the nth power the result will be a b n n k 0cn k an k bn where cn k n k n k and is read n CHOOSE k equals n factorial divided by k factorial n k factorial So a b 5 a5 5 a4 b 10 a3 b2 10 a2 b3 5 a1 b4 b5
1 Answer The coefficient of x3y2 in x 3y 5 is 90 Expansion of a b n gives us n 1 terms which are given by binomial expansion xnCra n r br where r ranges from n to 0 Note that powers of a and b add up to n and in the given problem this n 5 In x 3y 5 we need coefficient of x3y2 we have 3rd power of x and as such r 5 Explanation Given x a x b x c then expansion is x3 a b c x2 ab bc ac x abc x 3 3 x 3 x 3 x 3 with a b c 3 x 3 3 x3 9x2 27x 27 An alternate way to work it using binomial expansion
More picture related to x y 3 expansion
Solved The Taylor Expansion Of Y sinx Around 0 Is Sin Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/417/417dafd8-7346-4c49-b4ae-9f6f7c56ecfb/image

X Y
https://s2.studylib.net/store/data/017649587_1-bc9443a4f28c40866324738c51f3173a-768x994.png
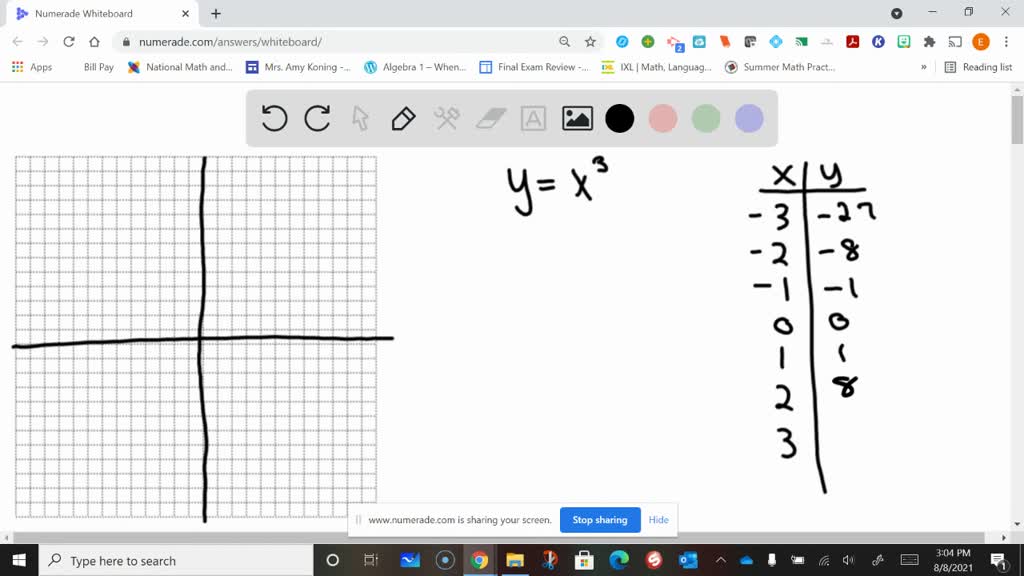
SOLVED Plot The Following Eurves y x 3 x
https://cdn.numerade.com/previews/474657b2-da79-4b5d-8159-3c623293a6ea_large.jpg
x y 4 x 4 y 4 z 4 4x 3y 4xy 3 4y 3z 4yz 3 4z 3x 4zx 3 6x 2y 2 6y 2z 2 6z 2x 2 12x 2yz 12xy 2z 12xyz 2 Note that a b 4 a 4 4a 3b 6a 2b 2 4ab 3 b 4 So we can find the terms of x y z 4 that only involve 2 of x y z by combining the expansions of binomial powers One way to see that Using the Binomial Theorem you can quickly calculate the 4th term or any kth term In trying to find the 4th term we let k 4 and in the binomial x y 10 the term a y and v 10 This gives us Use the Binomial Theorem 210x 4y 6 Using the Binomial Theorem you can quickly calculate the 4th term or any k th term
[desc-10] [desc-11]

PALACE X Y 3 22FW HN9887 LUCK D
https://static.luck-d.com/product/t/64603/thumb_PALACE_X_Y-3_TRACK_PANTS_BLACK_-_22FW_HN9887_1128085325401044.png

Zortrax GT2 Belt X Y long 1 Set 3DJake International
https://c-3d.niceshops.com/upload/image/product/large/default/1604.1024x1024.jpg
x y 3 expansion - [desc-14]

