what is the period of a 50 khz sine wave Formula The formula used to calculate the period of one cycle or revolution is Wave or Rotational Frequency T 1 f Angular Frequency T 2 radians T 360 degrees Symbols T Time period of 1 cycle f Frequency Angular frequency Pi constant Frequency Measured
The formula for period is T 1 f where T is period the time it takes for one cycle to complete and f is frequency To get period from frequency first convert frequency from Hertz to 1 s 1 Hz equals 1 s For basic sine and cosine functions the period is 2 pi This length can be measured in multiple ways In word problems and in other tricky circumstances it may be most useful to measure from peak to peak The following three waves have different periods To rank each wave by period from shortest to longest look at he distance
what is the period of a 50 khz sine wave
what is the period of a 50 khz sine wave
https://media.cheggcdn.com/media/a93/a9356059-5f09-43d7-acf3-1848163f0af6/phpzpUqID
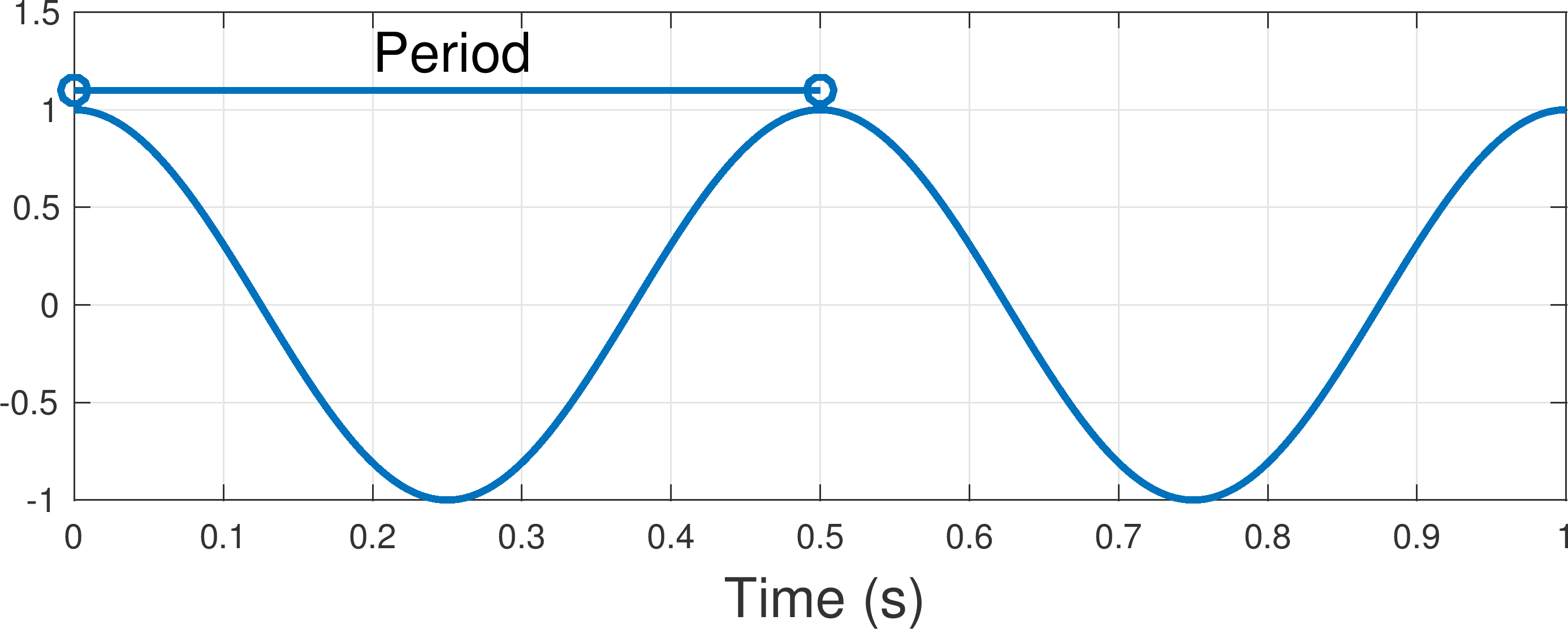
Waveform Period frequency
http://music-web2.ucsd.edu/~trsmyth/sinusoids171/img9.png
Solved Assuming The Carrier Frequency Is 100 KHz With A Peak Voltage
https://www.coursehero.com/qa/attachment/26268900/
This is the basic unchanged sine formula A 1 B 1 C 0 and D 0 So amplitude is 1 period is 2 there is no phase shift or vertical shift Example 2 sin 4 x 0 5 3 amplitude A 2 period 2 B 2 4 2 phase shift 0 5 or 0 5 to the right vertical shift D 3 In words The period of a 50 kHz sine wave is 2 x 10 5 second A sine wave looks like this The distance between two crests high points or two See full answer below
To write a sine function you simply need to use the following equation f x asin bx c d where a is the amplitude b is the period you can find the period by dividing the absolute value b by 2pi in your case I believe the frequency and period are the same c is the phase shift or the shift along the x axis and d is the vertical The frequency of a wave is 10 Hz What is its period The period of the wave is 100 s The period of the wave is 10 s The period of the wave is 0 01 s The period of the wave is 0 1 s
More picture related to what is the period of a 50 khz sine wave

How To Find The Amplitude Period And Frequency Of A Trigonometric
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/ow-to-find-the-amplitude-period-and-frequency-of-a-trigonometric-functi-01-1620209825.png

A Simple 60 Hz Sine Wave Is Shown With The Amplitude Peak to peak
https://www.researchgate.net/profile/Stephen-Hanly-2/publication/318827258/figure/download/fig8/AS:522561763987456@1501599841448/A-simple-60-Hz-sine-wave-is-shown-with-the-amplitude-peak-to-peak-RMS-frequency-and.png
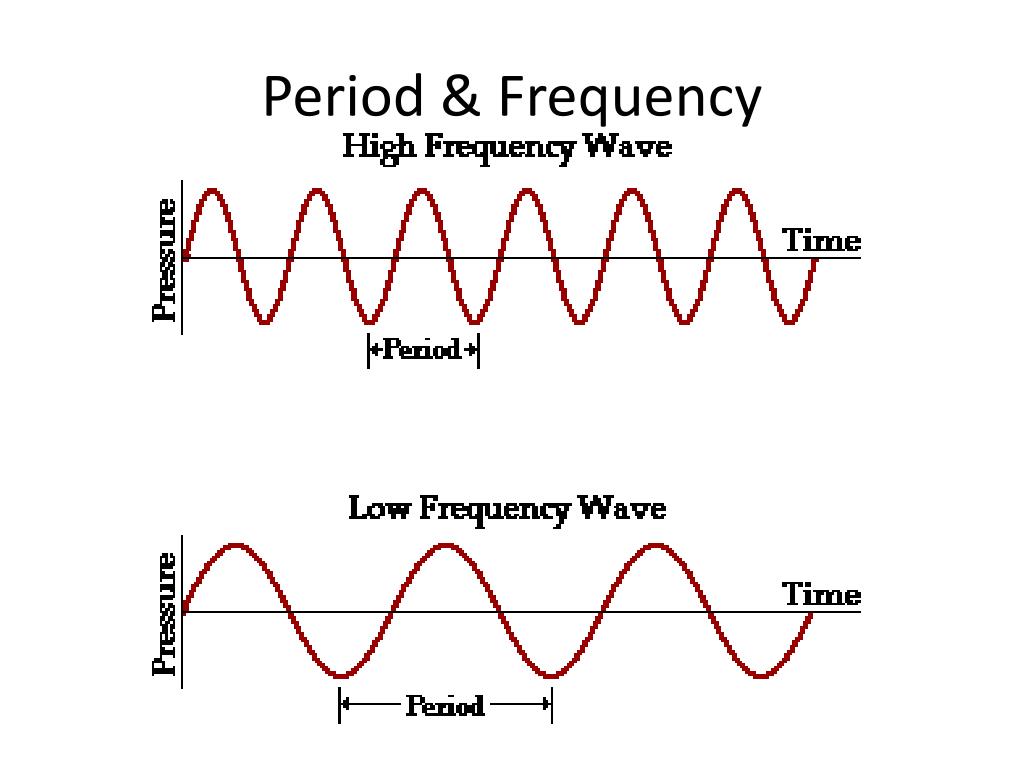
How To Find Frequency With Number Of Waves And Time Haiper
https://image.slideserve.com/718698/period-frequency-l.jpg
Formula T Wave Speed Frequency Wave Speed Where T Sine Wave Period Wavelength Example A sine wave with 5m wavelength and 8ms 1 speed will have a frequency of Frequency 8 5 Frequency 1 6 Hz The period would be T Detailed Solution Download Solution PDF Concept The frequency of a sin wave given the time period is given by f 1 T The time period is therefore T 1 f This is explained with the help of the following diagram Calculation Given frequency of sin wave 50 kHz The time period will be
Normally the period of sin x would be 2pi long Lets compare sin 4x and sin x At x 1 sin x sin 1 sin 4x sin 4 At x 2 sin x sin 2 sin 4x sin 8 As you can see in sin x x goes up by plus 1 every time 0 1 2 3 4 On the other hand sin 4x x goes up by plus 4 every time 0 4 8 12 16 It has an amplitude of 3 8 cm a frequency of 51 2 Hz and a distance from a crest to the neighboring trough of 12 8 cm Determine the period of such a wave See Answer Answer 0 0195 sec

How To Calculate Wave Period
https://www.learntocalculate.com/wp-content/uploads/2020/05/WAVEPERIOD-1.png
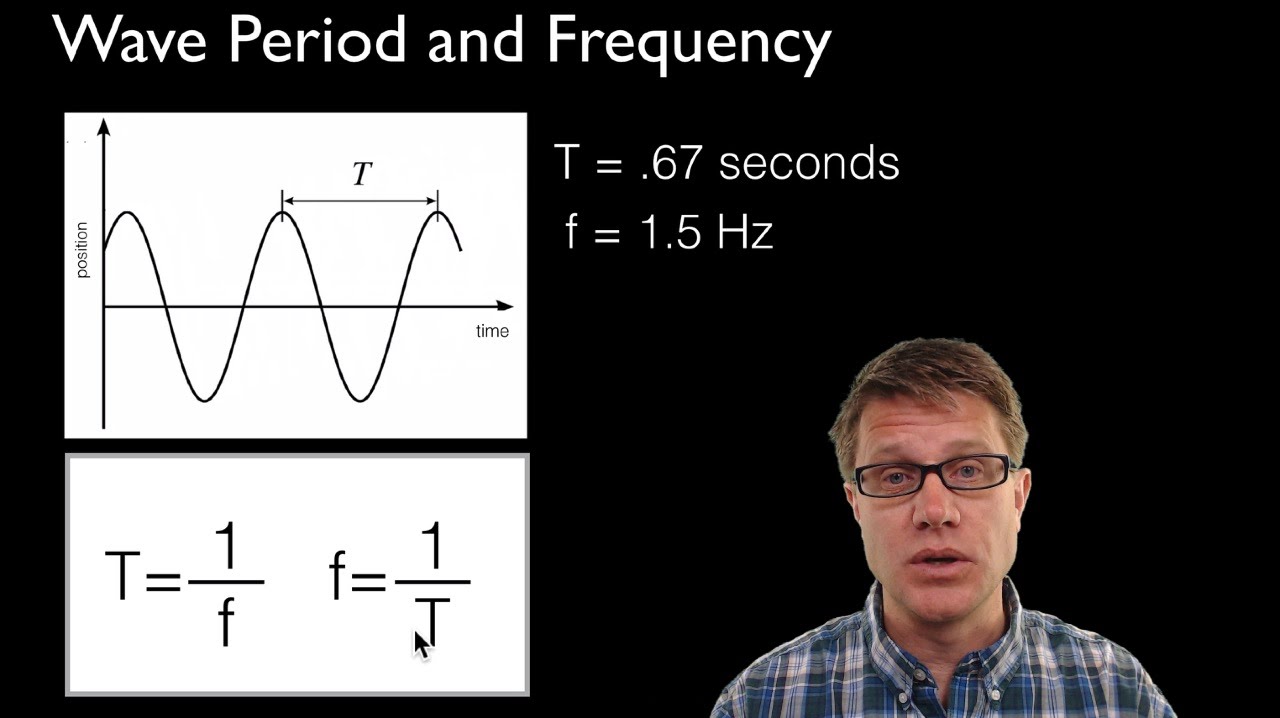
Wave Period And Frequency YouTube
https://i.ytimg.com/vi/v3CvAW8BDHI/maxresdefault.jpg
what is the period of a 50 khz sine wave - The period of a 50 kHz sine wave is 2 x 10 5 second A sine wave looks like this The distance between two crests high points or two See full answer below
