transformation matrix explained Transformation matrix Central object in linear algebra mapping vectors to vectors In linear algebra linear transformations can be represented by matrices If is a linear transformation mapping to and is a column vector with entries then for some matrix called the transformation matrix of citation needed
A transformation matrix is a square matrix which represents a linear transformation in vector space It transforms from one coordinated system to a different system by keeping the nature of that space identical Transformations and Matrices A matrix can do geometric transformations Have a play with this 2D transformation app Matrices can also do 3D transformations transform from 3D to 2D very useful for computer graphics and much much more
transformation matrix explained

transformation matrix explained
https://i1.rgstatic.net/publication/338618288_An_Explanation_for_the_Diagonally_Predominant_Property_of_the_Positive_Symmetric_Ensemble_Transform_Matrix/links/5e661f65a6fdcc37dd11e036/largepreview.png

TommyG TV Episode 23 The Transformation Matrix Explained YouTube
https://i.ytimg.com/vi/HLgcV858NnM/maxresdefault.jpg

Question Video Determining Linear Transformation Using Matrix
https://media.nagwa.com/163170286564/en/thumbnail_l.jpeg
How do I transform a point using a matrix A point x y in a 2D plane can be transformed on to another point x y by a matrix M x y is the object and x y is the image The coordinates of the image point can be found using matrix multiplication To transform x y by the matrix A transformation T is linear if T v w T v T w and T cv cT v for all vectors v and w and for all scalars c Equivalently T cv dw cT v dT w for all vectors v and w and scalars c and d It s worth noticing that T 0 0 because if not it couldn t be true that T c0 cT 0
Working with transformation matrices is the basic step for various fields like robotics aerospace autonomous driving epipolar geometry etc In this article we saw several concepts namely frame of reference convention right v s left handed systems The geometry of 2 2 matrix transformations The preview activity demonstrates how the matrix 1 0 0 1 defines a matrix transformation that has the effect of reflecting 2 dimensional vectors in the horizontal axis
More picture related to transformation matrix explained

How To Write Transformation Matrix In Matlab Mohammad has Mcintosh
https://i.ytimg.com/vi/09I15RO49vg/maxresdefault.jpg

Transformation Matrix Definition Formula Applications Examples
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/transformation-matrix-1633533700.png

Minecraft Transformation Effect On Craiyon
https://pics.craiyon.com/2023-09-25/2ed42aace5654464967319297de516ca.webp
This section introduced matrix transformations functions that are defined by matrix vector multiplication such as T xvec A xvec for some matrix A text If A is an m times n matrix then T real n to real m text Find the matrix of a linear transformation with respect to the standard basis Determine the action of a linear transformation on a vector in mathbb R n It turns out that this is always the case for linear transformations
[desc-10] [desc-11]
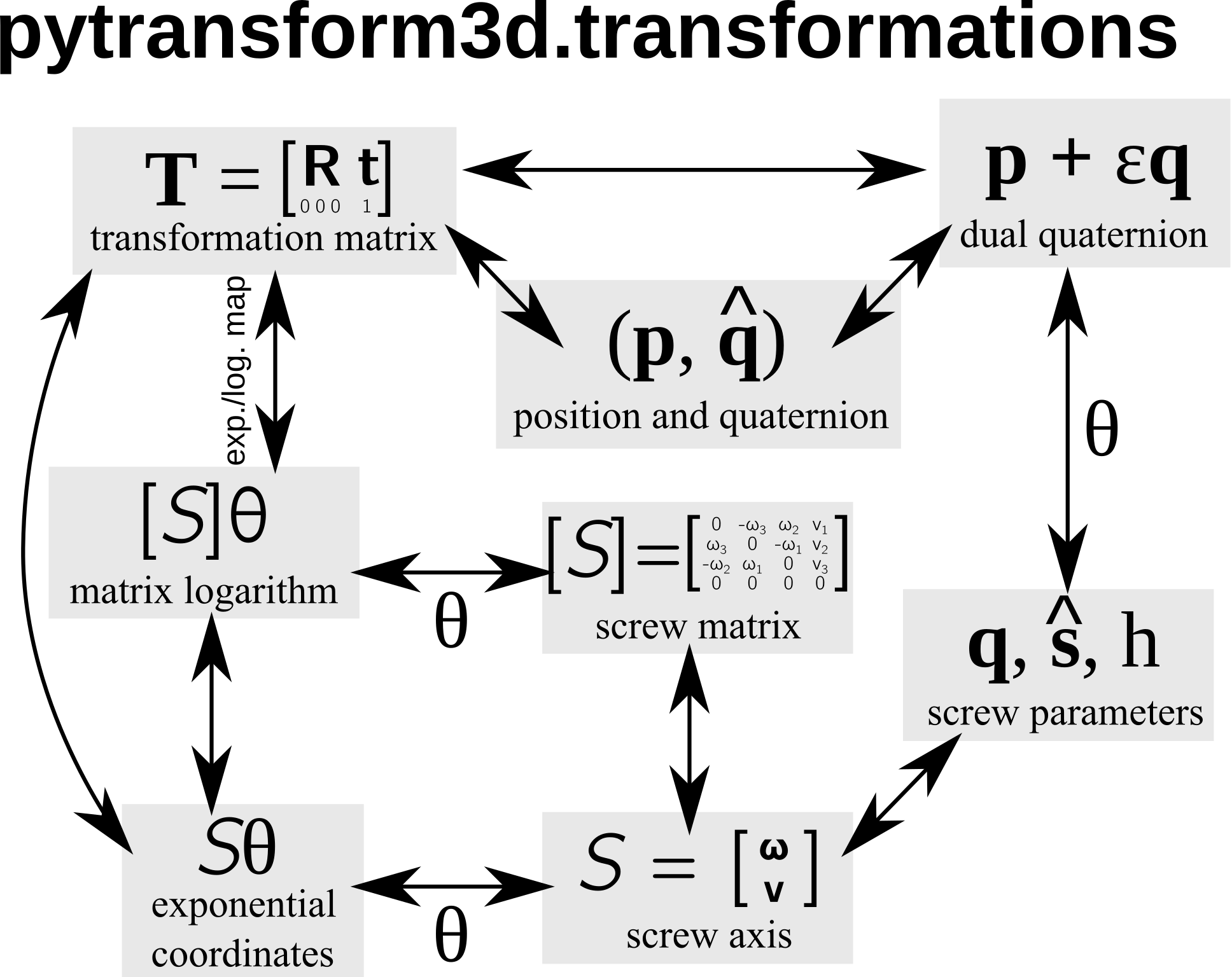
SE 3 3D Transformations Pytransform3d 3 1 0 Documentation
https://dfki-ric.github.io/pytransform3d/_images/transformations.png

PDF Single Real Transformation Matrix Application For Asymmetrical
https://i1.rgstatic.net/publication/262450243_Single_real_transformation_matrix_application_for_asymmetrical_three-phase_lines/links/02e7e537c9750698a8000000/largepreview.png
transformation matrix explained - How do I transform a point using a matrix A point x y in a 2D plane can be transformed on to another point x y by a matrix M x y is the object and x y is the image The coordinates of the image point can be found using matrix multiplication To transform x y by the matrix