sum and product rule polynomials Below is a summary of the steps we used to find the product of two polynomials using the distributive property How To Given the multiplication of two polynomials use the distributive property to simplify the expression Multiply each term of the first polynomial by each term of the second Combine like terms Simplify
To summarize multiplying a polynomial by a monomial involves the distributive property and the product rule for exponents Multiply all of the terms of the polynomial by the monomial For each term multiply the coefficients and add exponents of variables where the bases are the same The rule of sum Addition Principle and the rule of product Multiplication Principle are stated as below Rule of Sum Statement If there are n choices for one action and m choices for another action and the two actions cannot be done at the same time then there are n m ways to choose one of these actions
sum and product rule polynomials

sum and product rule polynomials
https://hi-static.z-dn.net/files/d68/a5363ea52551686e5e38becbe7d22fe4.jpg

Complex Analysis Product Rule And Polynomial Mathematics Stack Exchange
https://i.stack.imgur.com/Mti10.png
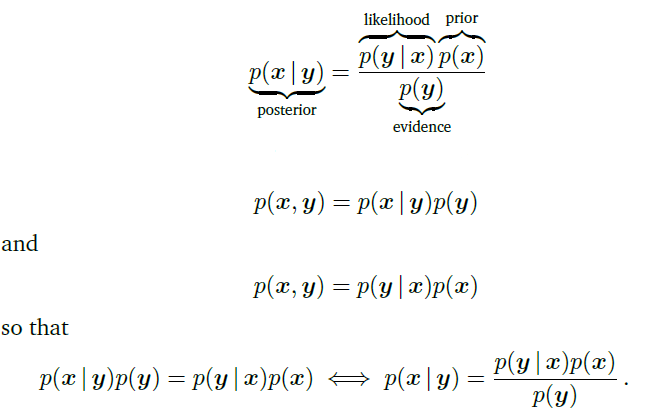
4 3 Sum Rule Product Rule And Bayes Theorem
https://1.bp.blogspot.com/-goXZWrh1XzY/YTx753fO1LI/AAAAAAAAGso/WHotUfvQDZUJNNW26N8uhMAO7Ku8gtQ3QCLcBGAsYHQ/s645/svd.png
You are usually required to find the sum or product of the roots of the second equation The strategy is to use identities which contain and where and are the roots of the first quadratic If you know the values of and from the first quadratic you can use them to help find the sum or product of the new roots About this unit This topic covers Adding subtracting and multiplying polynomial expressions Factoring polynomial expressions as the product of linear factors Dividing polynomial expressions Proving polynomials identities Solving polynomial equations finding the zeros of polynomial functions Graphing polynomial functions
Sum and Product Rules of Roots 12 1 10 1 1 according to remainder factor theorems 1 is a root x Il x 10 12 11 21 10 51 Example Write a quadratic equation with zeros 3 51 and 3 Method 1 Using sum and productnfle of roots SUM of the roots 3 3 PRODUCT ofthe roots 3 15i 25i 9 25 Sum of roots We ve already found the sum and product of alpha and beta so we can substitute as follows alpha 2 beta 2 3 5 2 2xx 2 5 17 25 d We add our fractions 1 alpha 1 beta as follows 1 alpha 1 beta beta alpha alpha beta alpha beta alpha beta We know the sum top and product bottom so we can simply write
More picture related to sum and product rule polynomials
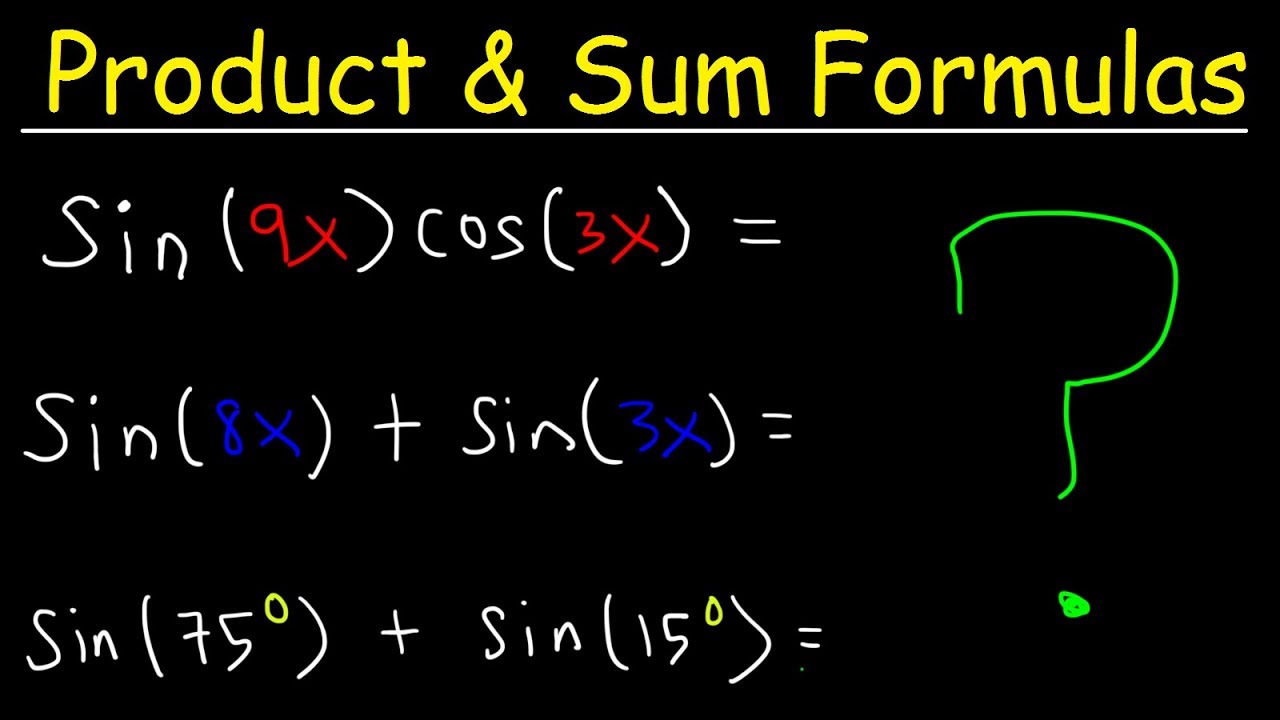
Product To Sum Identities And Sum To Product Formulas Trigonometry
https://i.ytimg.com/vi/8Prc7VGt40w/maxresdefault.jpg

The Sum And Product Of The Roots Of A Quadratic Equation 1 To 5 YouTube
https://i.ytimg.com/vi/GY6O5EleIOA/maxresdefault.jpg

Differentiating Polynomials Using The Power Rule With A Combination Of
https://study.com/cimages/videopreview/videopreview-full/losb7ug8dq.jpg
By the quadratic formulas the two roots can be represented as Sum of the Roots r1 r2 Product of the Roots r1 r2 The sum of the roots of a quadratic equation is equal to the negation of the coefficient of the second term divided by the leading coefficient Vieta s formula relates the coefficients of polynomials to the sums and products of their roots as well as the products of the roots taken in groups For example if there is a quadratic polynomial f x x 2 2x 15 it will have roots of x 5 and x 3 because f x x 2 2x 15 x 3 x 5
Polynomials Multiply Special Products Objective Recognize and use special product rules of a sum and differ ence and perfect squares to multiply polynomials There are a few shortcuts that we can take when multiplying polynomials If we can recognize them the shortcuts can help us arrive at the solution much quicker Sum of roots b a b a product of roots c a c a As you can see from the work below when you are trying to solve a quadratic equations in the form of ax2 bx c a x 2 b x c The sum and product of the roots can be rewritten using the two formulas above

When To Use Product And Sum Rules Solving Genetics Problems YouTube
https://i.ytimg.com/vi/0sQPlDE0FCc/maxresdefault.jpg

10 Adding Polynomials Worksheet With Answers Worksheeto
https://www.worksheeto.com/postpic/2015/02/kuta-software-infinite-algebra-1-multiplying-polynomials_315508.png
sum and product rule polynomials - 1 asked Oct 3 2016 at 0 34 J doe 1 417 1 17 31 Add a comment 2 Answers Sorted by 2 Writing p z z a1 z an p z z a 1 z a n you simply find p z d dzp z p z d d z p z If you use the product rule fg f g fg f g f g f g on each linear factor you arrive at the equation