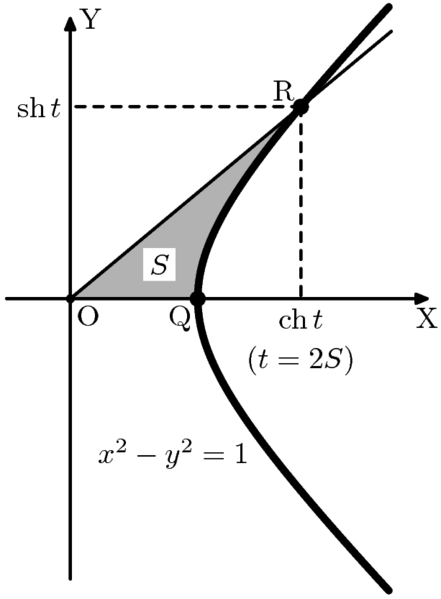
state the definition of the hyperbolic cosine and hyperbolic sine functions The hyperbolic functions may be defined as solutions of differential equations The hyperbolic sine and cosine are the solution s c of the system c x s x s x c x displaystyle begin aligned c x s x s x c x end aligned
The two basic hyperbolic functions are sinh and cosh Hyperbolic Sine sinh x e x e x 2 pronounced shine Hyperbolic Cosine cosh x e x e x 2 pronounced cosh They use the natural exponential function e x And are not the same as sin x and cos x but a little bit similar sinh vs sin cosh vs cos Catenary The hyperbolic sine function is a function f R R is defined by f x e x e x 2 and it is denoted by sinh x Sinh x ex e x 2 Graph y Sinh x Hyperbolic Cosine Function The hyperbolic cosine function is a function f R R is defined by f x e x e x 2 and it is denoted by cosh x cosh x ex e x 2
state the definition of the hyperbolic cosine and hyperbolic sine functions

state the definition of the hyperbolic cosine and hyperbolic sine functions
https://image2.slideserve.com/3997128/slide4-l.jpg
Hyperbolic Functions Explained
https://elliptigon.com/content/images/2019/06/441px-Hyperbola-hyperbolic_functions-1.png

Hyperbolic Functions
http://www.sosmath.com/trig/hyper/hyper01/img12.gif
As you can see in Figure PageIndex 4 we define the hyperbolic cosine to be the x value of this terminal point and the hyperbolic sine as the y value We denote these functions as cosh s and sinh s respectively Definition of the hyperbolic cosine for a complex argument In the complex plane the function is defined by the same formula that is used for real values Here are two graphics showing the real and imaginary parts of the hyperbolic cosine function over the
Definition 4 11 1 Hyperbolic Cosines and Sines The hyperbolic cosine is the function cosh x e x e x over2 and the hyperbolic sine is the function sinh x e x e x over 2 The hyperbolic sine function is easily defined as the half difference of two exponential functions in the points and After comparison with the famous Euler formula for sine it is easy to derive the following representation of the hyperbolic sine through the circular sine
More picture related to state the definition of the hyperbolic cosine and hyperbolic sine functions
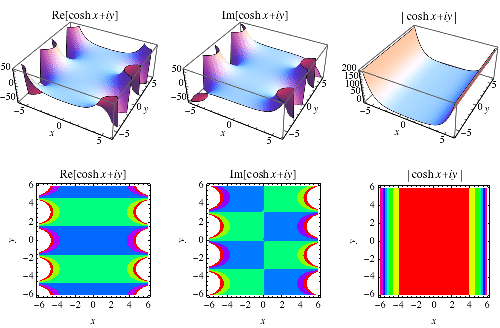
Hyperbolic Cosine From Wolfram MathWorld
https://mathworld.wolfram.com/images/interactive/CoshReImAbs.gif
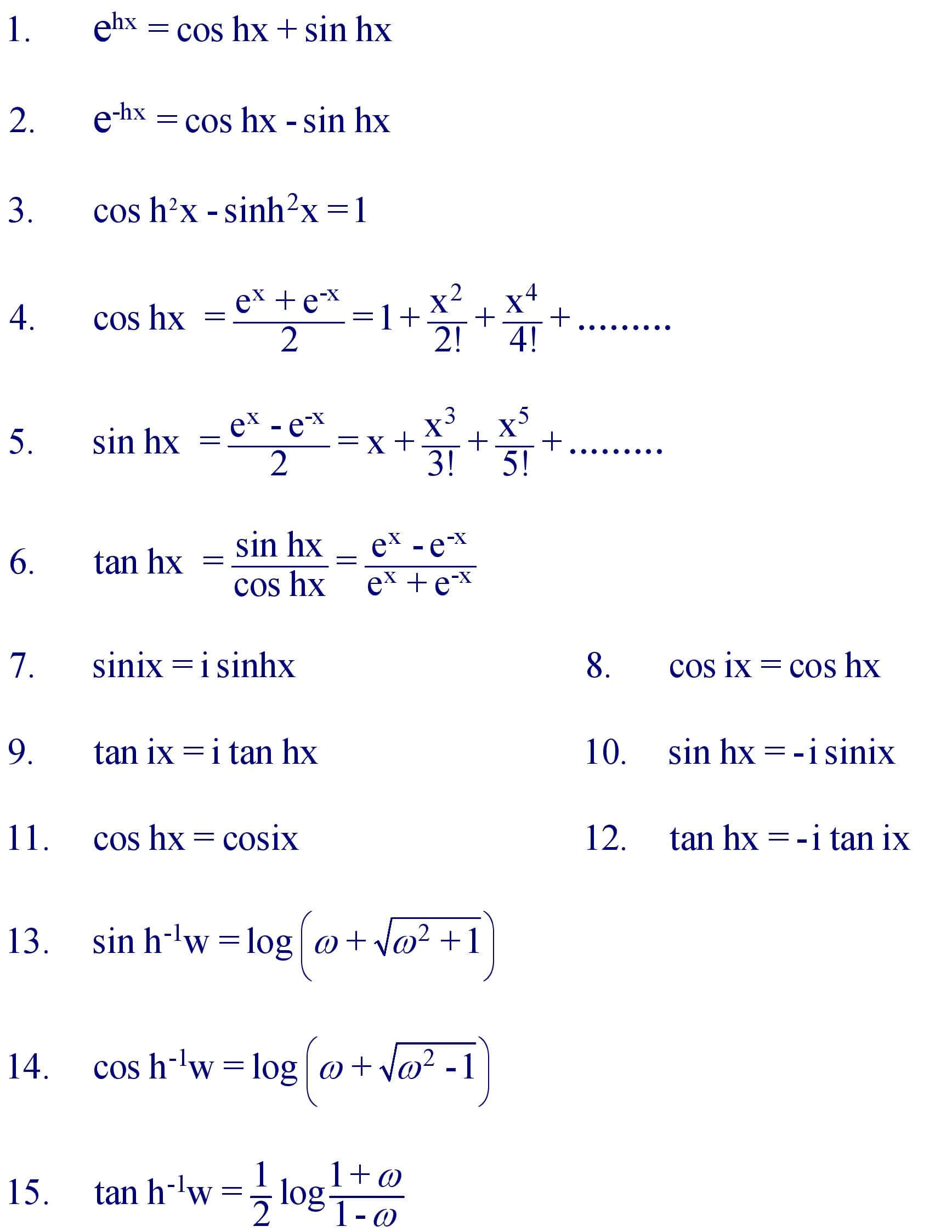
Hyperbolic Functions Formula Formula In Maths
http://formulainmaths.in/wp-content/uploads/2023/04/Hyper-page-001.jpg

Hyperbolic Function By Circle Team Issuu
https://image.isu.pub/120905092656-9818b9ebd4c34cc786a6af98c153397c/jpg/page_1.jpg
The six well known hyperbolic functions are the hyperbolic sine hyperbolic cosine hyperbolic tangent hyperbolic cotangent hyperbolic cosecant and hyperbolic secant They are among the most used elementary functions The hyperbolic cosine and sine functions are defined in terms of the exponential function by cosh x frac exp x exp x 2 quad quad and sinh x frac exp x exp x 2 Because the two functions may be represented hypergeometrically as the sums
Where sinh a is the hyperbolic sine of a All six hyperbolic functions can now be defined in general analogous to the trigonometric circular functions The graphs of the hyperbolic functions are shown below Hyperbolic sine and cosine The hyperbolic sine is de ned as ex e x sinh x 2 1 where x 2 R is a real variable y 2 1 6 5 4 3 2 1 0 1 2 3 4 5 6 1 x sinh x Figure 1 Hyperbolic sine as x 2 2 5 2 5 The hyperbolic cosine is de ned as 1 ex e x cosh x 2 2 x 2 R y 6 5 4 3 2 1 cosh x x 2 1 0 1 2

The Hyperbolic Trigonometric Functions Extend The Notion Of The
https://i.pinimg.com/originals/f8/55/62/f855620facf3bf541d8b0439b9a91b19.png
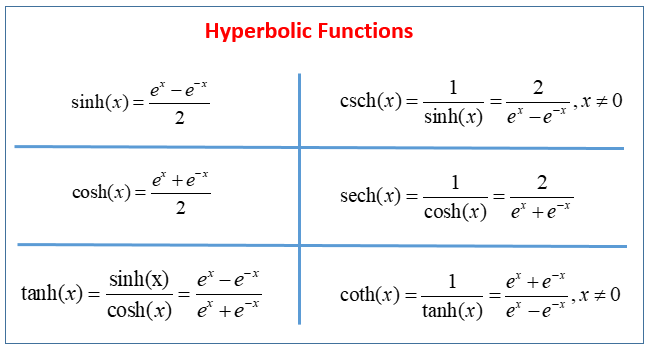
Hyperbolic Functions solutions Examples Videos
https://www.onlinemathlearning.com/image-files/hyperbolic-functions.png
state the definition of the hyperbolic cosine and hyperbolic sine functions - Definition of the hyperbolic cosine for a complex argument In the complex plane the function is defined by the same formula that is used for real values Here are two graphics showing the real and imaginary parts of the hyperbolic cosine function over the