square root of 338 Guess what the square root of the irrational number is For example if your irrational number is 2 you might guess 1 2 Divide the initial irrational number by the guessed number For example 2 divided by 1 2 is 1 67 Add the resulting sum to the original guessed number For example 1 67 plus 1 2 is 2 87
If the question is about using the square root directly against the equation the answer is definitely NO However with certain transformation of a given equation into a different but equivalent form it is possible Here is the idea Assume for example the same equation as analyzed in the previous answer x 2 x 63 Sqrt 138 39019777 3321584 11 74734012447073 The prime factorisation of 138 is 138 2 3 23 Since this contains no squared terms the square root cannot be simplified and not being a perfect square it is irrational Note that 11 2 121 138 144 12 2 So sqrt 138 is somewhere between 11 and 12 closer to 12 Let us approximate it as 11 3 4 47 4 This is
square root of 338

square root of 338
https://i.ytimg.com/vi/m5sj_ee7NlQ/maxresdefault.jpg

Square Root Of 338 ROOTSC
https://i2.wp.com/wmznlejcfq.s3-ap-southeast-1.amazonaws.com/media/square-roots/square-root-of-338-by-long-division-method.png
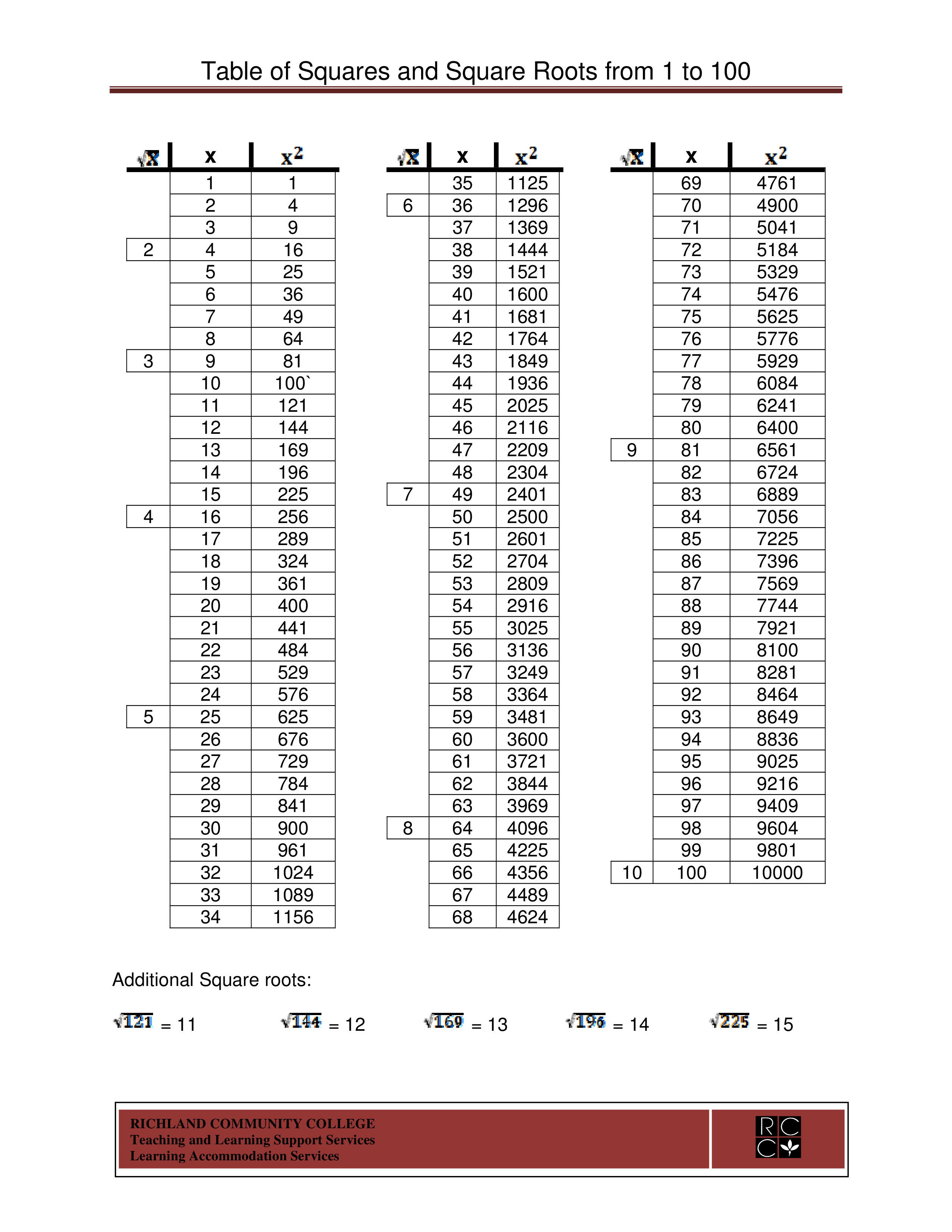
Square Root Number Chart Templates At Allbusinesstemplates
https://www.allbusinesstemplates.com/thumbs/abbfbcd8-4909-4147-bd7a-f767ea5d11f7_1.png
The principal square root of minus one is i It has another square root i I really dislike the expression the square root of minus one Like all non zero numbers 1 has two square roots which we call i and i If x is a Real number then x 2 0 so we need to look beyond the Real numbers to find a square root of 1 Complex numbers can be thought of as The square root of 1 3 is an irrational number that can be written as color blue 1 sqrt 3 Explanation You could use a calculator to find the approximate value of this namely 0 5773502692 but since 1 sqrt 3 is irrational this is not exact
The square roots of 64 are 8i and 8i where i is the imaginary unit satisfying i 2 1 The square of any Real number is non negative so to find a square root for 64 we need to look beyond the Real number line to Complex numbers The imaginary unit i is a number whose square is 1 So it is a square root of 1 Note that i is also a square root of 1 satisfying i 2 To extract square root of such numbers a if n is even just take the square root of x and 10n and multiply them and b if n is odd mutiply x by 10 and reduce n by 1 to make it even and then take square root of each and multiply them Hence See process and examples below In scientific notation numbers are written in the form x xx10 n
More picture related to square root of 338
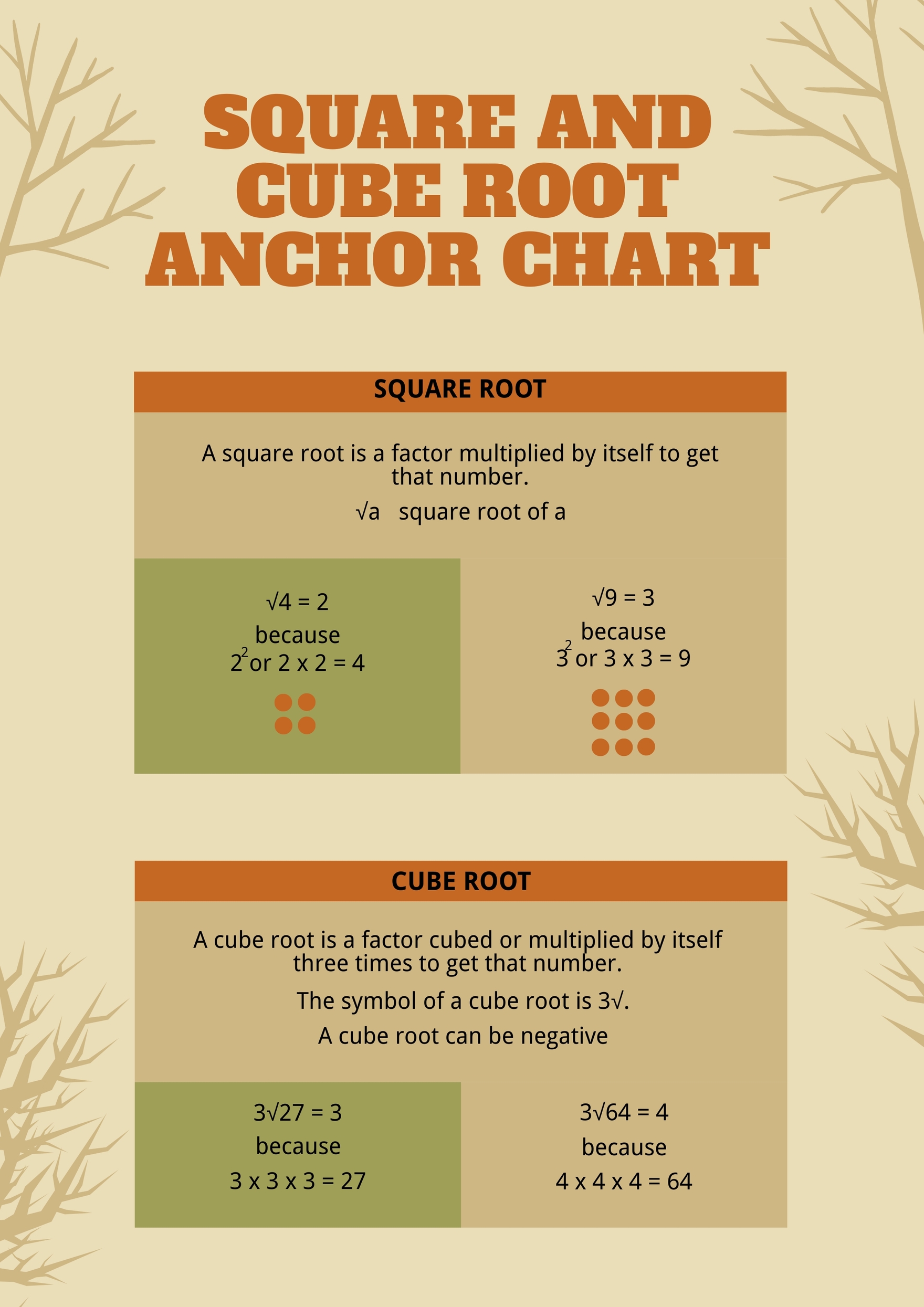
Square And Cube Root Anchor Chart In Illustrator PDF Download
https://images.template.net/113858/square-and-cube-root-anchor-chart-ty39e.jpeg
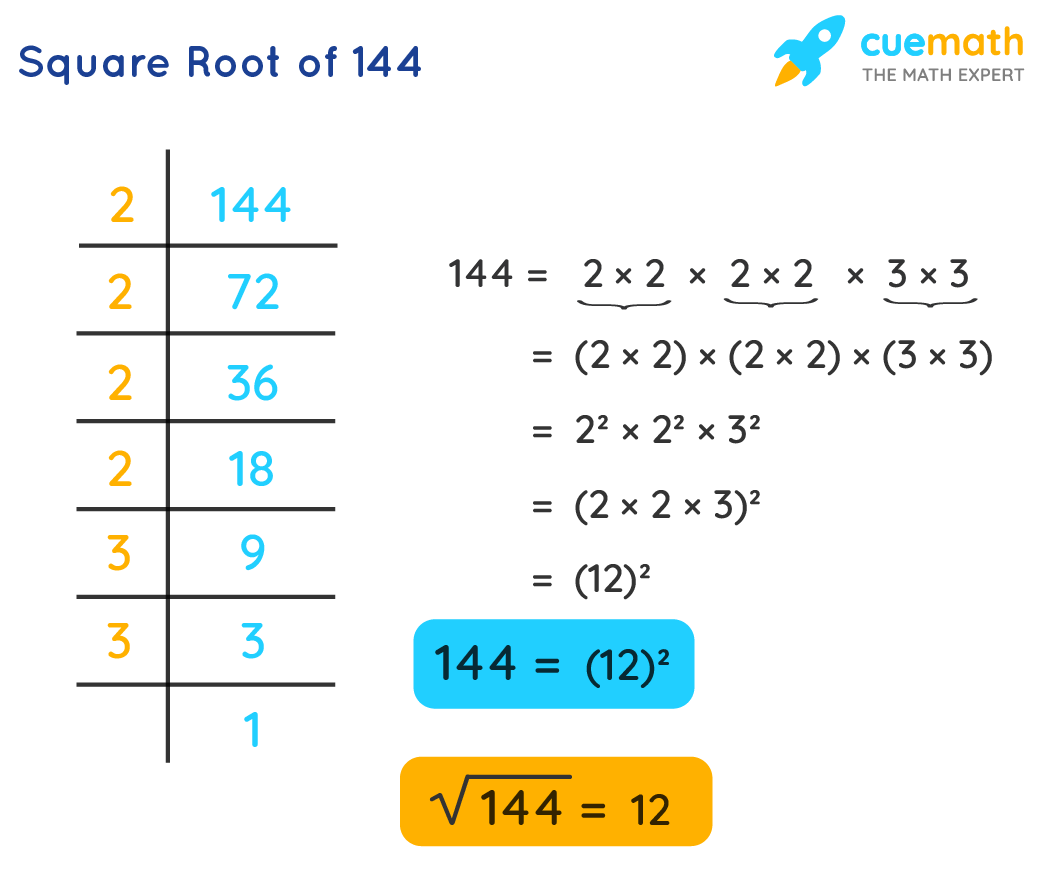
26 72 Square Root Calculator ReshnaPercy
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/square-root-calculator-1630045127.png
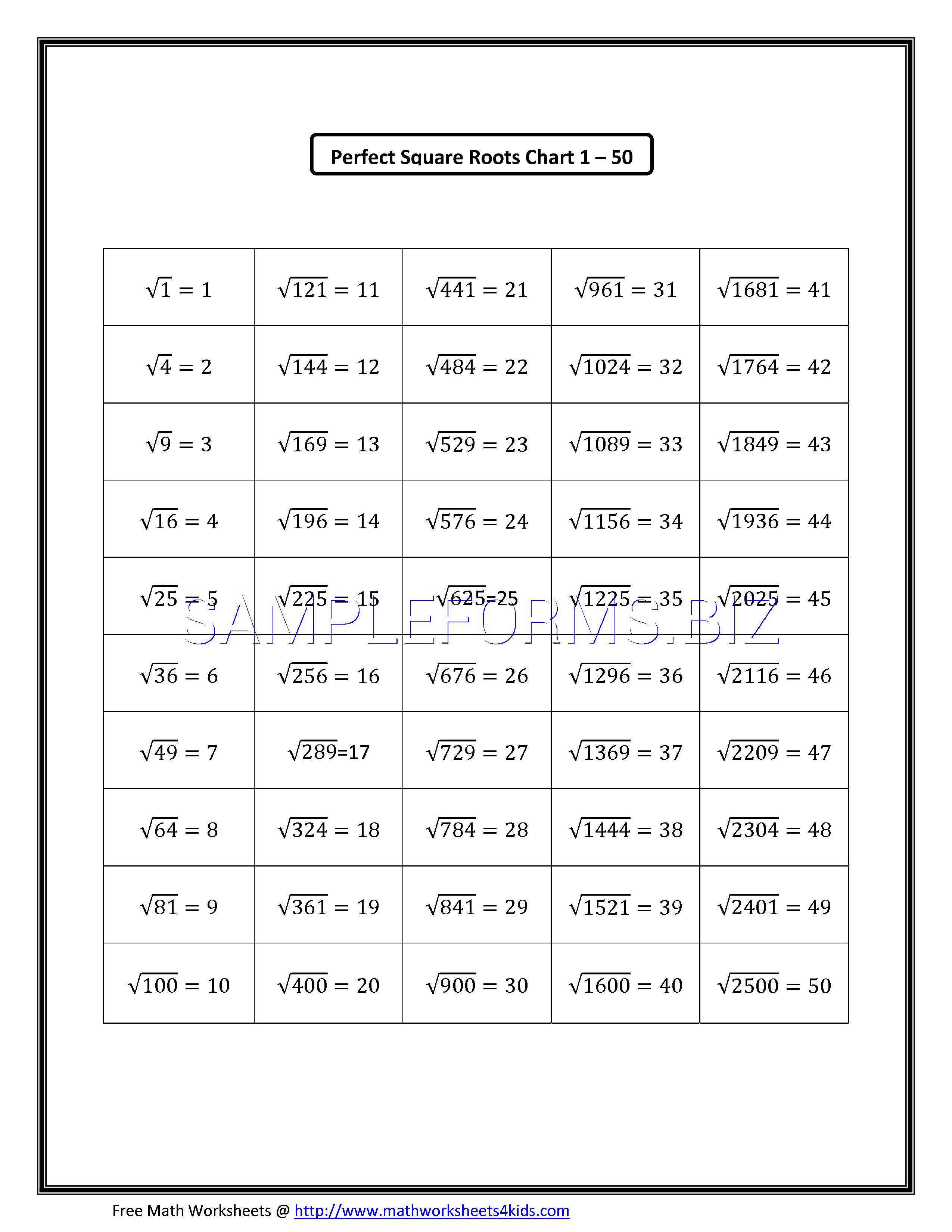
F x x 2 x 2 u
http://square-root-chart.sampleforms.biz/perfect-square-roots-chart-1-50/1.gif
First rewrite the expression as sqrt x 3 sqrt x 2 x Then use this rule of radicals to simplify the expression In fact you can multiply two odd or two even numbers using squares adding subtracting and halving as follows a b a b 2 2 a b 2 2 For example 23 27 252 22 625 4 621 361 19 2 so sqrt 361 19 See explanation for a few methods Prime Factorisation One of the best ways to attempt to find the square
[desc-10] [desc-11]

Cube Root 1 To 30 Value Of Cube Roots From 1 To 30 PDF
https://wmznlejcfq.s3-ap-southeast-1.amazonaws.com/media/square-roots/cube-root-1-to-30.png

How To Find The Roots Of A Quadratic Equation with Pictures
http://www.wikihow.com/images/f/f1/Find-the-Roots-of-a-Quadratic-Equation-Step-3.jpg
square root of 338 - To extract square root of such numbers a if n is even just take the square root of x and 10n and multiply them and b if n is odd mutiply x by 10 and reduce n by 1 to make it even and then take square root of each and multiply them Hence See process and examples below In scientific notation numbers are written in the form x xx10 n