sin cos tan formula Sine Cosine and Tangent Sine Cosine and Tangent often shortened to sin cos and tan are each a ratio of sides of a right angled triangle For a given angle each ratio stays the same no matter how big or small the triangle is To calculate them Divide the length of one side by another side
In trigonometry formulas we will learn all the basic formulas based on trigonometry ratios sin cos tan and identities as per Class 10 11 and 12 syllabi Also find the downloadable PDF of trigonometric formulas at BYJU S Sin Cos Tan Formula The three ratios i e sine cosine and tangent have their individual formulas Suppose ABC is a right triangle right angled at B as shown in the figure below Now as per sine cosine and tangent formulas we have here Sine Opposite side Hypotenuse BC AC Cos Adjacent side Hypotenuse AB AC
sin cos tan formula
sin cos tan formula
https://qph.fs.quoracdn.net/main-qimg-0596dc9aaf911d8ff9fd42ace758160a

What Are Sin Cos Tan SOHCAHTOA With Examples Teachoo Finding
https://d77da31580fbc8944c00-52b01ccbcfe56047120eec75d9cb2cbd.ssl.cf6.rackcdn.com/9b93e28b-7857-44a1-bcd9-d2a1e7ce3c89/3-how-to-learn-sin-cos-tan-trigonometry-formula-sohcahtoa.jpg
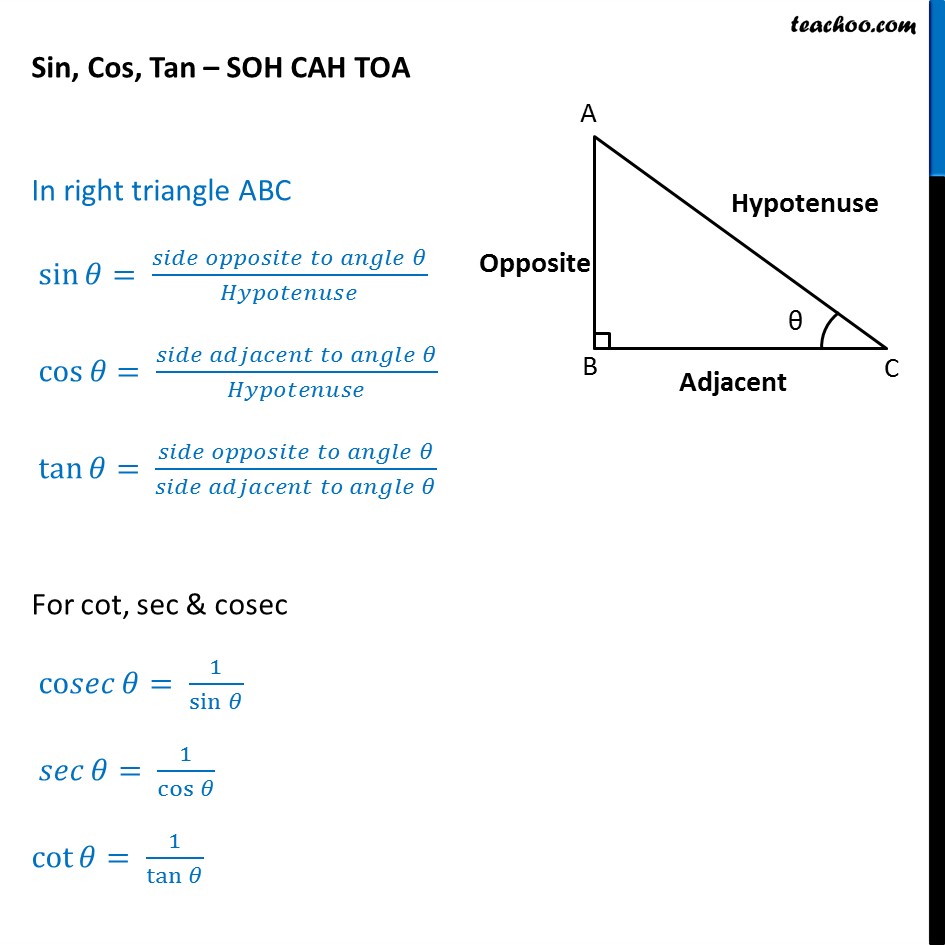
What Are Sin Cos Tan SOHCAHTOA With Examples Teachoo
https://d1avenlh0i1xmr.cloudfront.net/2d209857-8f8f-4d60-b4ab-cde4d519a591/1-what-are-sin-cos-tan.jpg
The important sin cos tan formulas with respect to the above figure are sin A Opposite side Hypotenuse BC AB cos A Adjacent side Hypotenuse AC AB tan A Opposite side Adjacent side BC AC We can derive some other sin cos tan formulas using these definitions of sin cos and tan functions Basic Trig Ratio Formulas formulas relating to the basic trigonometric ratios sin cos tan etc Reciprocal Identities formulas dealing with the reciprocal relationship between trig ratios Trigonometric Ratio Table Trigonometry values are depicted for standard angles in the trigonometry table
When we divide Sine by Cosine we get sin cos Opposite Hypotenuse Adjacent Hypotenuse Opposite Adjacent tan So we can say tan sin cos That is our first Trigonometric Identity Cosecant Secant and Cotangent We can also divide the other way around such as Adjacent Opposite instead of Opposite Adjacent Three common trigonometric ratios are the sine sin cosine cos and tangent tan These are defined for acute angle A below adjacent opposite hypotenuse sin A opposite hypotenuse cos A adjacent hypotenuse tan
More picture related to sin cos tan formula
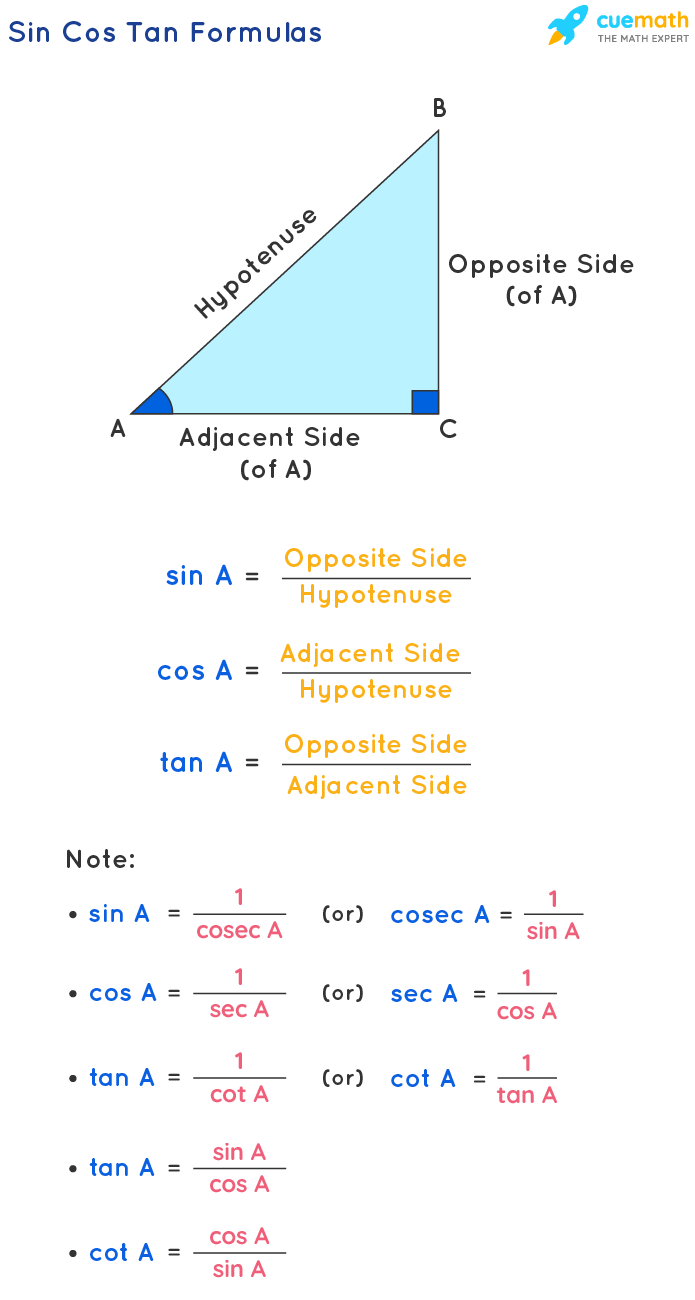
Sin Cos Tan Formulas What Are Sin Cos Tan Formulas Examples
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/formulas-related-to-sin-cos-and-tan-1623752098.png

Basic Trigonometry A Quick Recap Finding Value Of Trignometric Fun
https://d1avenlh0i1xmr.cloudfront.net/262adc14-157c-400e-9195-9d725c10ffc8/basic-trigonometry--quick-recap.jpg

What Are Sin Cos Tan SOHCAHTOA With Examples Teachoo
https://d1avenlh0i1xmr.cloudfront.net/6db1be00-2c4e-4c41-a4be-c5ccf01fea3f/2-example-on-finding-sin-cos-tan-cosec-sec-cot.jpg
Solving sinusoidal equations of the form sin x d Unit 1 Right triangles trigonometry 0 700 Mastery points Ratios in right triangles Introduction to the trigonometric ratios Solving for a side in a right triangle using the trigonometric ratios
[desc-10] [desc-11]

Sin Cos Tan Adjacent Cos En Geometry Hypotenuse Math Sin Tan
https://34c771.medialib.edu.glogster.com/eB19K5T0o24UXwCc0E5K/screenshots/6j63ab4hjv1keojltv9sbei/1433089166-source.jpg
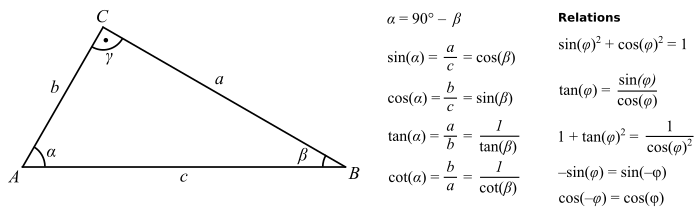
Sin Cos Tan Formulas
http://www.scitk.org/subsides/Formal_Science/Mathematics/sinus_cosinus/files/02_right_triangle.png
sin cos tan formula - When we divide Sine by Cosine we get sin cos Opposite Hypotenuse Adjacent Hypotenuse Opposite Adjacent tan So we can say tan sin cos That is our first Trigonometric Identity Cosecant Secant and Cotangent We can also divide the other way around such as Adjacent Opposite instead of Opposite Adjacent