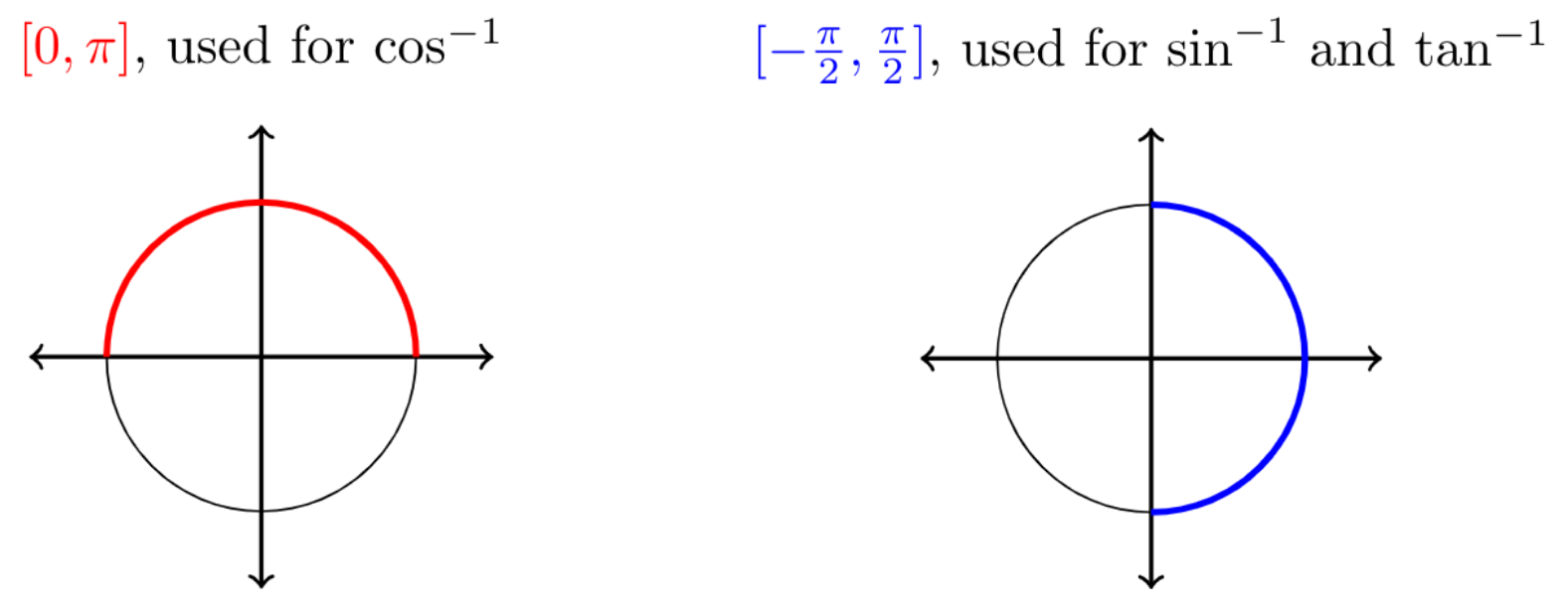
restrictions for inverse trig functions The domain of an inverse function is the range of the original function and the range of an inverse function is the domain of the original function Because the trigonometric functions are not one to one on their natural domains inverse trigonometric functions are defined for restricted domains
Inverse Trigonometric functions We know from their graphs that none of the trigonometric functions are one to one over their entire domains However we can restrict those functions to subsets of their domains where they are one to one For example y sin x is one to one over the interval left frac pi 2 frac pi 2 right Because the trigonometric functions are not one to one on their natural domains their domains are restricted so that inverse trigonometric functions can be defined for them For any trigonometric function f x if x f 1 y then f x y
restrictions for inverse trig functions

restrictions for inverse trig functions
https://i.ytimg.com/vi/ovyx6Ip0Id8/maxresdefault.jpg

Inverse Trigonometric Values
https://cdn1.byjus.com/wp-content/uploads/2020/04/principal-values-of-inverse-trig-functions2.png

Limits Of Inverse Trigonometric Functions Calculus YouTube
https://i.ytimg.com/vi/UPUzKShJPuk/maxresdefault.jpg
Trigonometry Inverse trigonometric functions Restricting domains of functions to make them invertible Google Classroom About Transcript Sal is given the graph of a trigonometric function and he discusses ways in which he can change the function to make it invertible Created by Sal Khan Questions Tips Thanks Since none of the six trigonometric functions are one to one they must be restricted in order to have inverse functions Therefore the result ranges of the inverse functions are proper i e strict subsets of the domains of the original functions
There are two generally accepted ways make these choices which restrict the domains of these functions so that they are one to one One approach simplifies the Trigonometry associated with the inverse functions but complicates the Calculus the other makes the Calculus easier but the Trigonometry less so We present both points of view Learn about arcsine arccosine and arctangent and how they can be used to solve for a missing angle in right triangles Let s take a look at a new type of trigonometry problem Interestingly these problems can t be solved with sine cosine or tangent
More picture related to restrictions for inverse trig functions
Chapter 3 Trigonometric Identities And Equations
https://mathbooks.unl.edu/PreCalculus/images/imagesChap13/range-inverse-trig.png

PPT B1 6 Derivatives Of Inverse Trig Functions PowerPoint
https://image1.slideserve.com/1708334/b-inverse-trig-as-functions-restrictions-l.jpg

Inverse Trig Functions Using Unit Circle YouTube
https://i.ytimg.com/vi/bKon2BMyl4s/maxresdefault.jpg
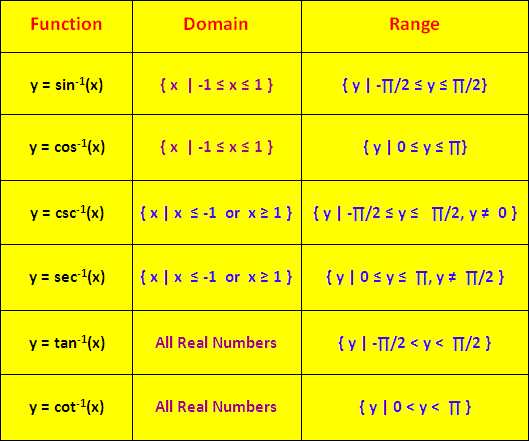
Since f x cos x is periodic to define an inverse function we must first restrict its domain so that there is a unique value of x for each value of y cos x By convention the arccosine function is the inverse of the restricted cosine function g x cos x 0 leq x leq pi which has domain 0 pi and range 1 1 If this property is applied to the trigonometric functions the following equations that deal with finding an inverse trig function of a trig function will only be true for values of x within the restricted domains sin 1 sin x
[desc-10] [desc-11]
Domain And Range Of Inverse Trigonometric Functions
https://www.onlinemath4all.com/images/DandRofITF.png.pagespeed.ce.Tm_apkKUsb.png

Limits At Infinity Of Inverse Trigonometric Functions How To Find
https://i.ytimg.com/vi/w5k_0uLPF-o/maxresdefault.jpg
restrictions for inverse trig functions - [desc-13]