log base rules Learn the eight 8 log rules or laws to help you evaluate expand condense and solve logarithmic equations Try out the log rules practice problems for an even better understanding
Key Takeaways Given any base b 0 and b 1 we can say that logb1 0 logbb 1 log1 bb 1 and that logb 1 b 1 The inverse properties of the logarithm are logbbx x and blogbx x where x 0 The product property of the logarithm allows us to write a product as a sum logb xy logbx logby Expand log 3 25 using the power rule for logs Solution Expressing the argument as a power we get log 3 25 log 3 5 2 Next we identify the exponent 2 and the base 5 and rewrite the equivalent expression by multiplying the exponent times the logarithm of the base log 3 25 2 log 3 5
log base rules

log base rules
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/log-or-logarithm-rules-1647317216.png

Basic Math Logarithms ENV710 Statistics Review Website
https://sites.nicholas.duke.edu/statsreview/files/2018/05/LogRules.png

Changing The Base Of Logarithms YouTube
https://i.ytimg.com/vi/qsc9IXxjwHE/maxresdefault.jpg
For simplicity we ll write the rules in terms of the natural logarithm ln x The rules apply for any logarithm log b x except that you have to replace any occurence of e with the new base b The natural log was defined by equations eqref naturalloga and eqref naturallogb Introduction to Logarithms In its simplest form a logarithm answers the question How many of one number multiply together to make another number Example How many 2 s multiply together to make 8 Answer 2 2 2 8 so we had to multiply 3 of the 2 s to get 8 So the logarithm is 3 How to Write it We write it like this log2 8 3
The laws of logarithms are algebraic rules that allow for the simplification and rearrangement of logarithmic expressions The 3 main logarithm laws are The Product Law log mn log m log n The Quotient Law log m n log m log n The Power Law log m k k log m Three basic logarithm rules are the product quotient and power rules Product rule The product rule of logarithms can be expressed as log b mn log b m log b n where b is the base and m and n are variables being multiplied Example Expand log 2 7x log 2 7x log 2 7 log 2 x Quotient rule
More picture related to log base rules
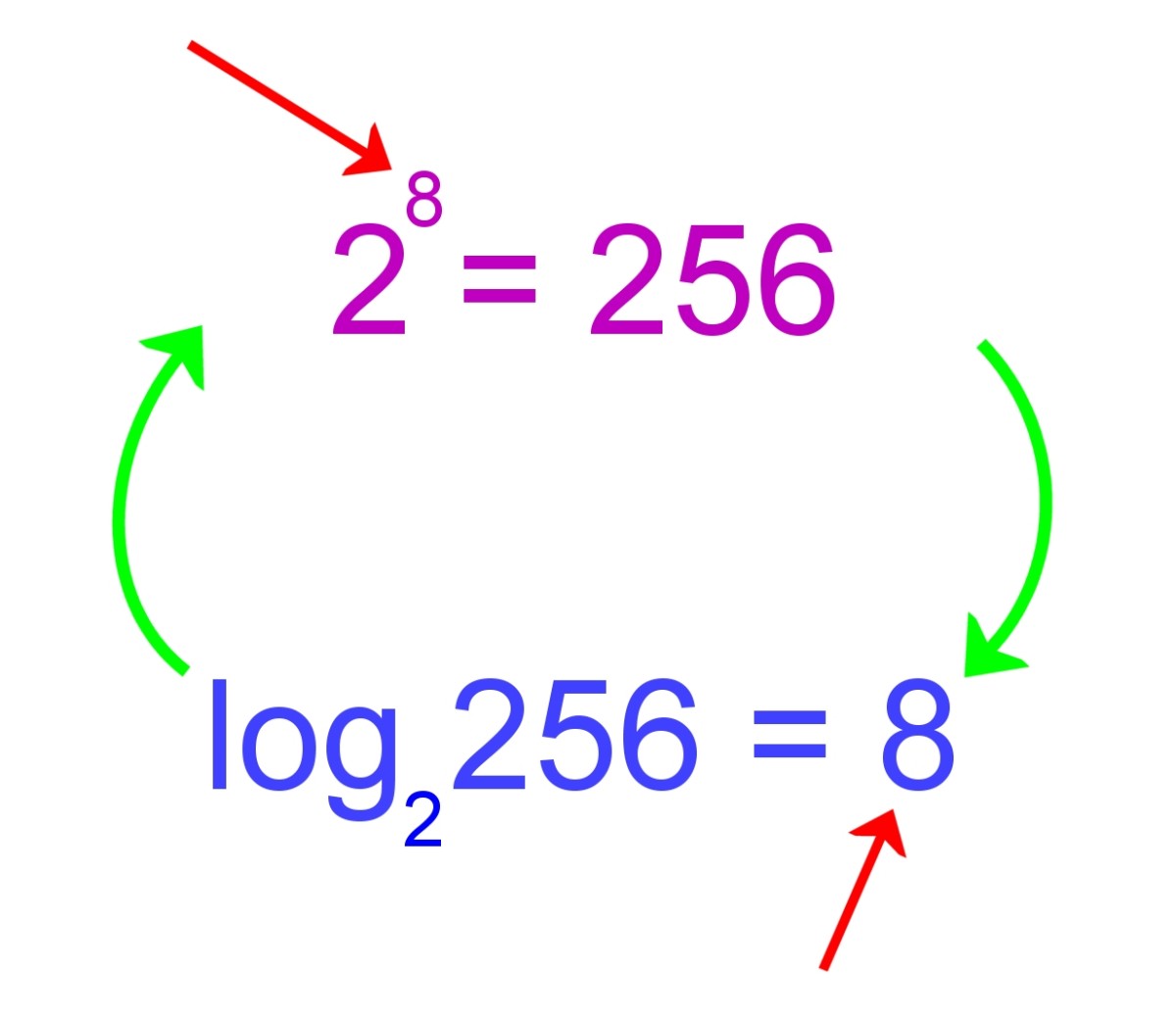
Rules Of Logarithms And Exponents A Guide For Students Owlcation
https://usercontent1.hubstatic.com/14476060_f520.jpg

Change Of Base Formula For Logarithms YouTube
https://i.ytimg.com/vi/xeBuUx86U4A/maxresdefault.jpg
Logarithmic Properties And Functions OER Commons
https://www.oercommons.org/editor/images/8229
Enhance your understanding of logarithmic functions and their practical applications through this detailed resource Explore the rules formulas and real life examples of the laws of logs empowering you to confidently manipulate logarithmic expressions A logarithm is the inverse of the exponential function Specifically a logarithm is the power to which a number the base must be raised to produce a given number For example log 2 64 6 log2 64 6 because 2 6 64 26 64 In general we have the following definition z z is the base x x logarithm of y y if and only if x z y xz y
[desc-10] [desc-11]
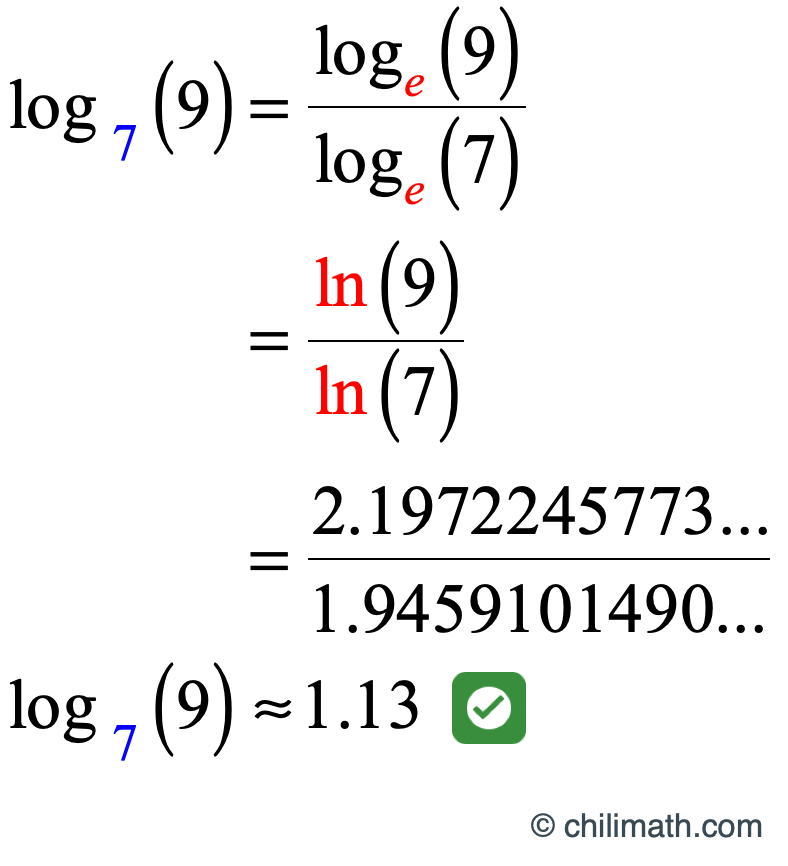
Change Of Base Formula Log Calculator
https://www.chilimath.com/wp-content/uploads/2020/04/example-4-change-of-base-formula.gif

Cambio De F rmula O Regla Base
https://www.mdematematicas.com/images/posts/3a745454b629a39c968e89e88b8f02fa-21.jpg
log base rules - The laws of logarithms are algebraic rules that allow for the simplification and rearrangement of logarithmic expressions The 3 main logarithm laws are The Product Law log mn log m log n The Quotient Law log m n log m log n The Power Law log m k k log m
