ln ln x rule The following are the rules of ln ln 1 0 ln e 1 ln m ln n ln mn ln m ln n ln m n ln a m m ln a e ln x x What are Log Derivative Rules Here are the derivatives of different types of logarithms The derivative of ln x is d dx ln x 1 x The derivative of log a x d dx log x 1 x ln a What are 4 Important
Ln ln x Natural Language Math Input Extended Keyboard Examples Upload Random Compute answers using Wolfram s breakthrough technology knowledgebase relied on by millions of students professionals For math science nutrition history geography engineering mathematics linguistics sports finance music The rule you re talking about is ln x ln y ln xy Also most of the times I ve seen ln 2 x this is meant to denote ln x cdot ln x ln x 2 Share
ln ln x rule

ln ln x rule
https://i.ytimg.com/vi/mpxEc7x3rfc/maxresdefault.jpg

Evaluate The Limit As X Approaches Infinity For ln X 1 x L Hopital
https://i.ytimg.com/vi/EaJRhA91YaY/maxresdefault.jpg
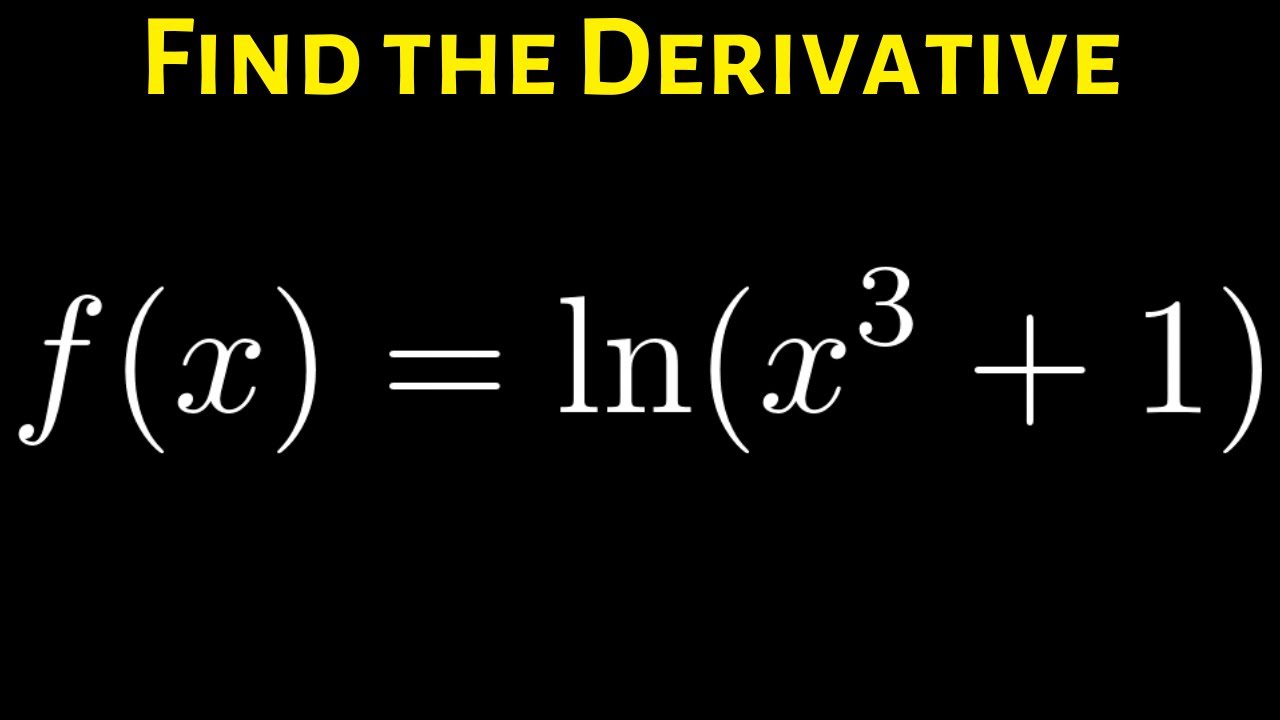
How To Find The Derivative Of F x Ln x 3 1 Using The Chain Rule
https://i.ytimg.com/vi/Fa2IlTP4hxM/maxresdefault.jpg
Definitions 1 log a x N means that a N x 2 log x means log 10 x All log a rules apply for log When a logarithm is written without a base it means common logarithm 3 ln x means log e x where e is about 2 718 All log a rules apply for ln When a logarithm is written ln it means natural logarithm The natural logarithm function is defined by ln x Integral on the interval 1 x of 1 x dt t for x 0 therefore the derivative of the natural logarithm is d dx ln x 1 x The natural logarithm is one of the most useful functions in mathematics with applications throughout the physical and biological sciences
As x approaches 0 ln x approaches As x approaches ln x approaches Natural logarithm rules properties Natural logarithms share the same basic logarithm rules as logarithms with other bases Product rule ln mn ln m ln n for x 0 and y 0 Quotient rule ln ln m ln n Power rule ln m n n ln m for x 0 In terms of natural logarithms this same rule is ln left frac x y right ln x ln y As with all log rules remember that we can use this equation in either direction If we start with something that matches the expression from the left side of the equation we can rewrite it like the right side of the equation or
More picture related to ln ln x rule
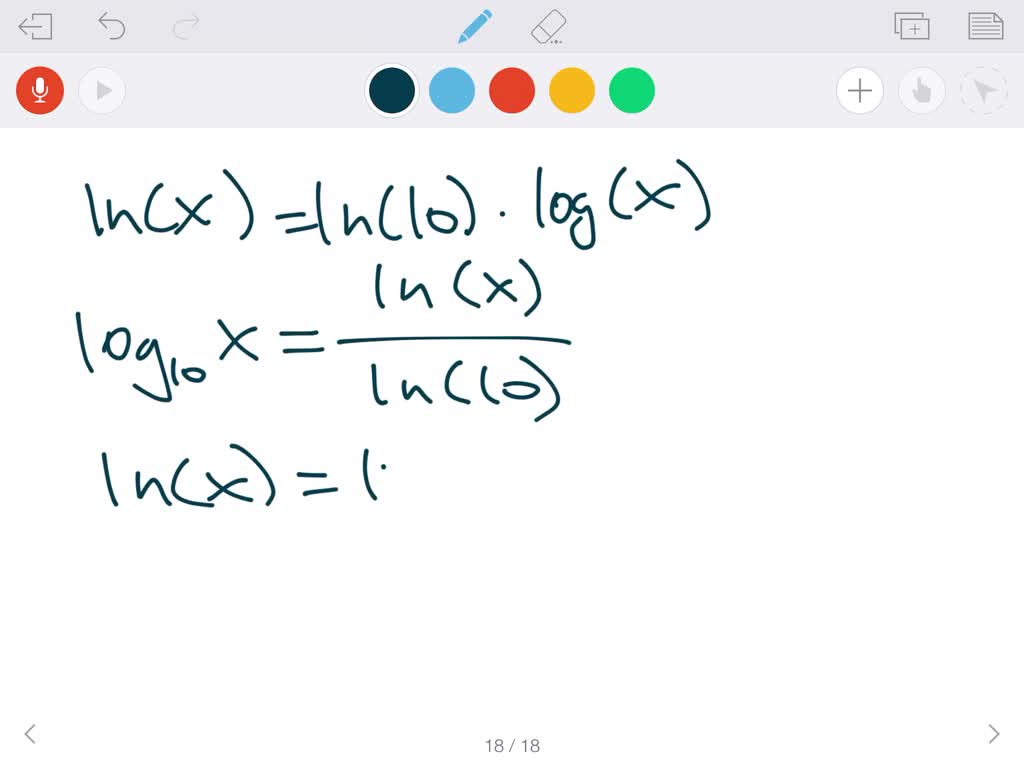
SOLVED Verify That Lnx ln10 logx And Discuss W H Y They re Numerade
https://cdn.numerade.com/previews/49fb0c1e-13be-457f-ba20-c006839b10ea_large.jpg

Derivative Of F x Ln 1 x 2 Math Videos F x Derivative
https://i.pinimg.com/originals/b4/5d/79/b45d790ce828efa0e5d3e141cf526d0f.jpg

Log Rules Narural Log Rules Rules Of Ln Logarithm Rules
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/log-or-logarithm-rules-1647317216.png
5 6 Laws of Logarithms Page ID Table of contents Learning Objectives The Product Rule for Logarithms Example 5 6 1 Caution Example 5 6 2 You Try 5 6 1 Using the Quotient Rule for Logarithms The Quotient Rule for Logarithms Ln x y y ln x ln 2 8 8 ln 2 Ln derivative f x ln x f x 1 x Ln integral ln x dx x ln x 1 C Ln of negative number ln x is undefined when x 0 Ln of zero
The natural logarithm of e itself ln e is 1 because e1 e while the natural logarithm of 1 is 0 since e0 1 The natural logarithm can be defined for any positive real number a as the area under the curve y 1 x from 1 to a 4 with the area being negative when 0 The relevant property here is that ln ab ln a ln b If you start from the property e xe y e x y you can take the natural log of both sides to get ln e xe y x y Now let e x a or x ln a and e y b or y ln b and substitute in to get ln ab ln a ln b
How To Calculate Natural Log The Tech Edvocate
https://www.thetechedvocate.org/wp-content/uploads/2023/09/a3p30142yj-1.jpg

Find The Derivative Of Ln ln 1 x The Derivative Of Logarithms YouTube
https://i.ytimg.com/vi/xXjAkeMB4Bw/maxresdefault.jpg
ln ln x rule - The natural logarithm function is defined by ln x Integral on the interval 1 x of 1 x dt t for x 0 therefore the derivative of the natural logarithm is d dx ln x 1 x The natural logarithm is one of the most useful functions in mathematics with applications throughout the physical and biological sciences