is negative square root of 5 a polynomial A special way of telling how many positive and negative roots a polynomial has A Polynomial looks like this Polynomials have roots zeros where they are equal to 0 Roots are at x 2 and x 4 It has 2 roots and both are positive 2 and 4 Sometimes we may not know where the roots are but we can say how many are positive or negative
What happens if you want to find the roots of a polynomial like this simplified one 3x 2 x 24 0 then the square root value becomes sqrt 1 2 4 cdot3 cdot24 sqrt 287 which is the square root of a negative number which isn t allowed What do you do in this case In particular for an expression to be a polynomial term it must contain no square roots of variables no fractional or negative powers on the variables and no variables in the denominators of any fractions Here are some examples This is NOT a polynomial term 6 x 2 because the variable has a negative exponent
is negative square root of 5 a polynomial

is negative square root of 5 a polynomial
https://i.ytimg.com/vi/wZpRqcCI8wY/maxresdefault.jpg
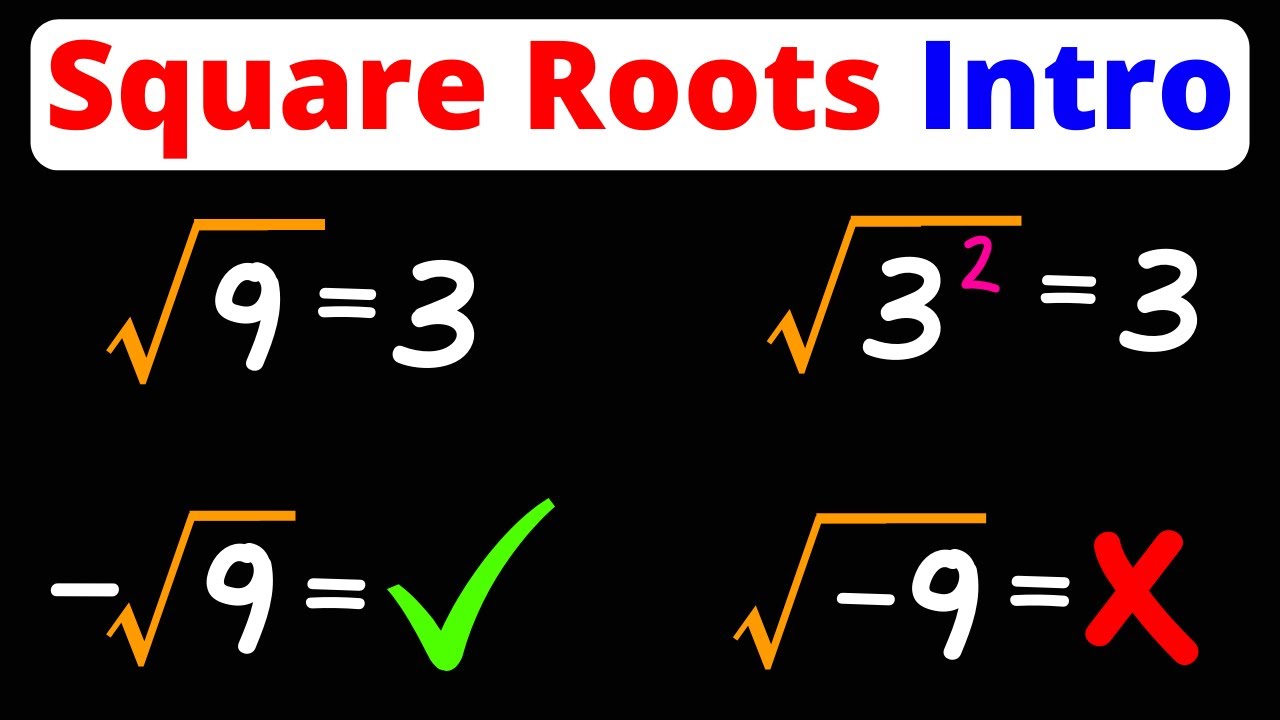
Square Roots Radicals Intro Positive Negative Examples Eat Pi
https://i.ytimg.com/vi/qkOb46oW_T4/maxresdefault.jpg
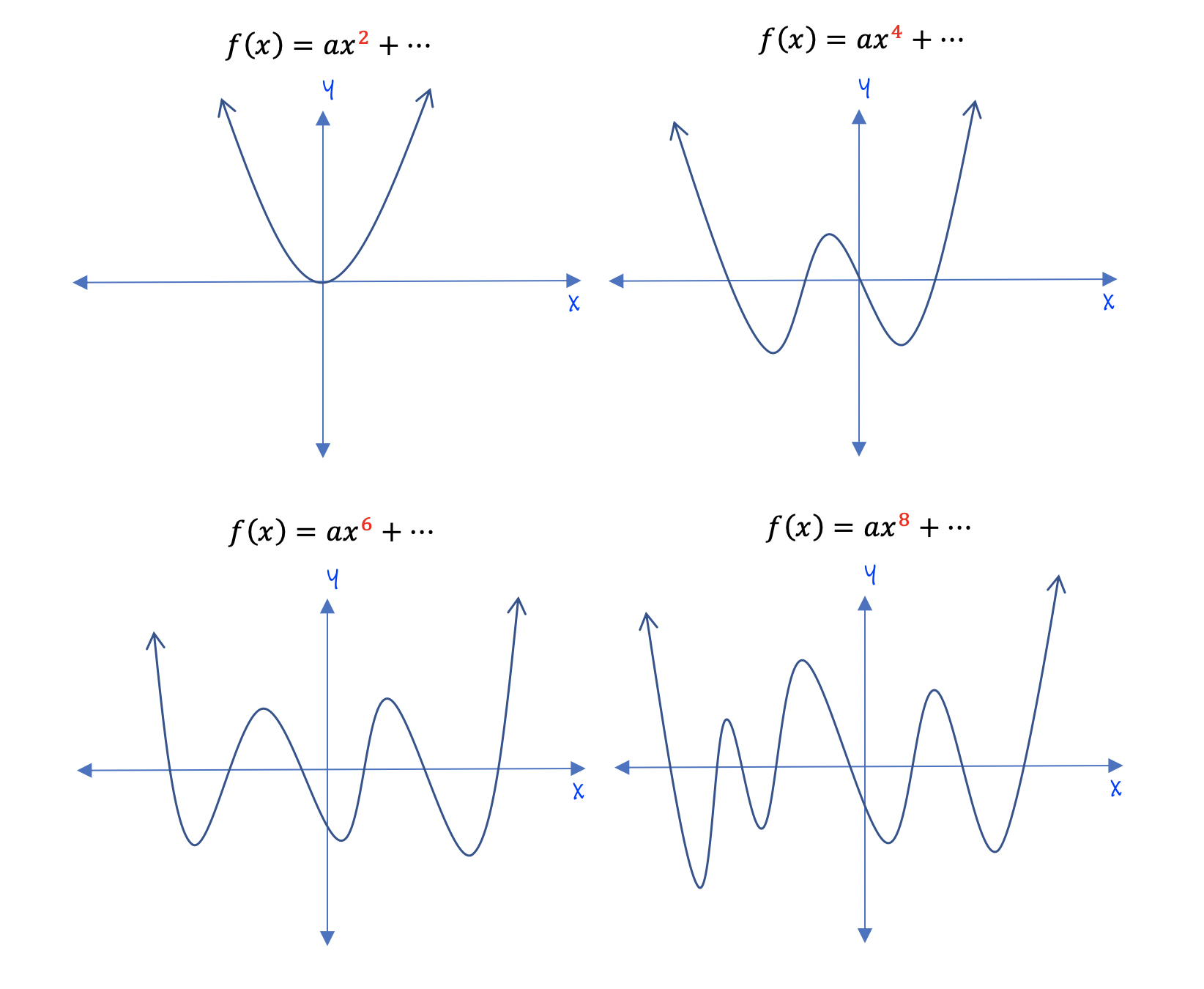
Graphs Of Polynomial Functions
https://jillwilliams.github.io/Graphs-of-Polynomial-Functions/images/pic6.png
If we want to find the negative square root of a number we place a negative in front of the radical sign For example sqrt 169 13 Because 0 2 0 sqrt 0 0 A root of a polynomial P z is a number z i such that P z i 0 The fundamental theorem of algebra states that a polynomial P z of degree n has n roots some of which may be degenerate For example the roots of the polynomial x 3 2x 2 x 2 x 2 x 1 x 1 1 are
To end up with a complex root from a polynomial you would have a factor like x 2 2 To solve this you would end take the square root of a negative and just as you would with the square root of a positive you would have to Free roots calculator find roots of any function step by step
More picture related to is negative square root of 5 a polynomial
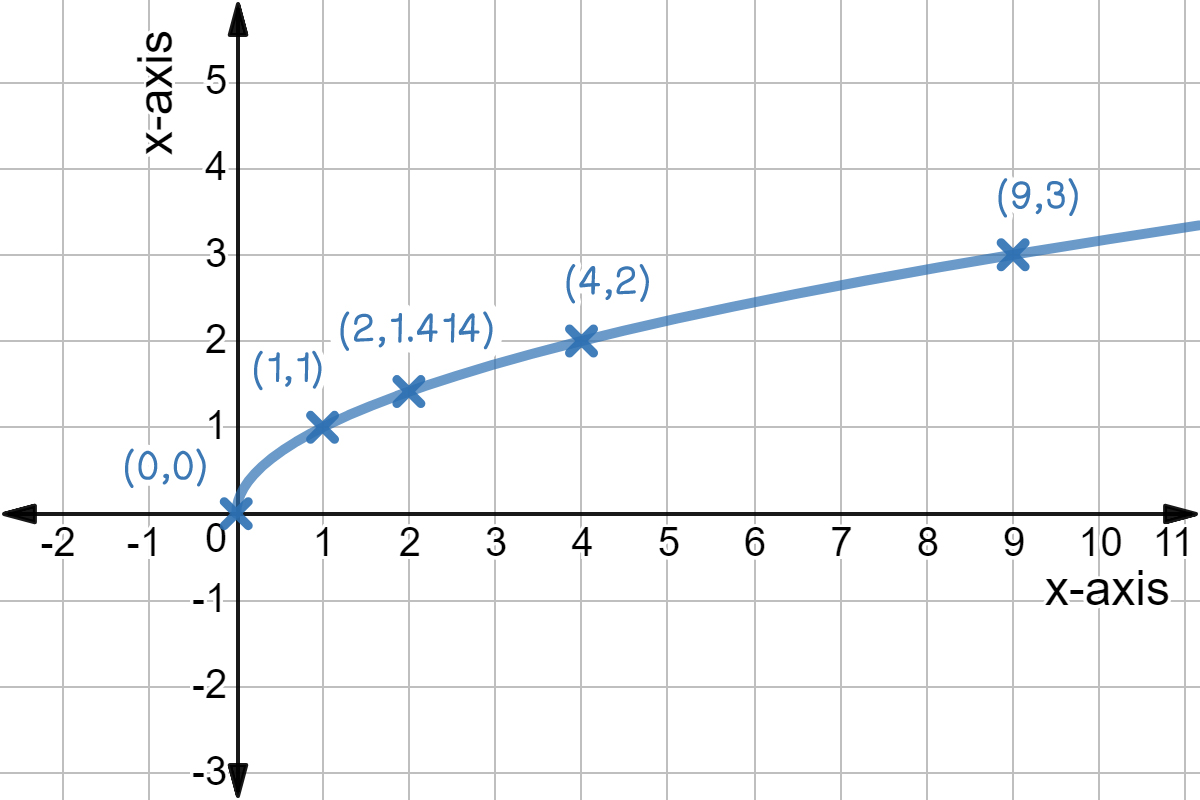
Square Root Function Graph Examples Practice Expii
https://d20khd7ddkh5ls.cloudfront.net/connect_points.jpeg

Question Video Determining If The Cube Root Of An Integer Is Rational
https://media.nagwa.com/272170952173/en/thumbnail_l.jpeg
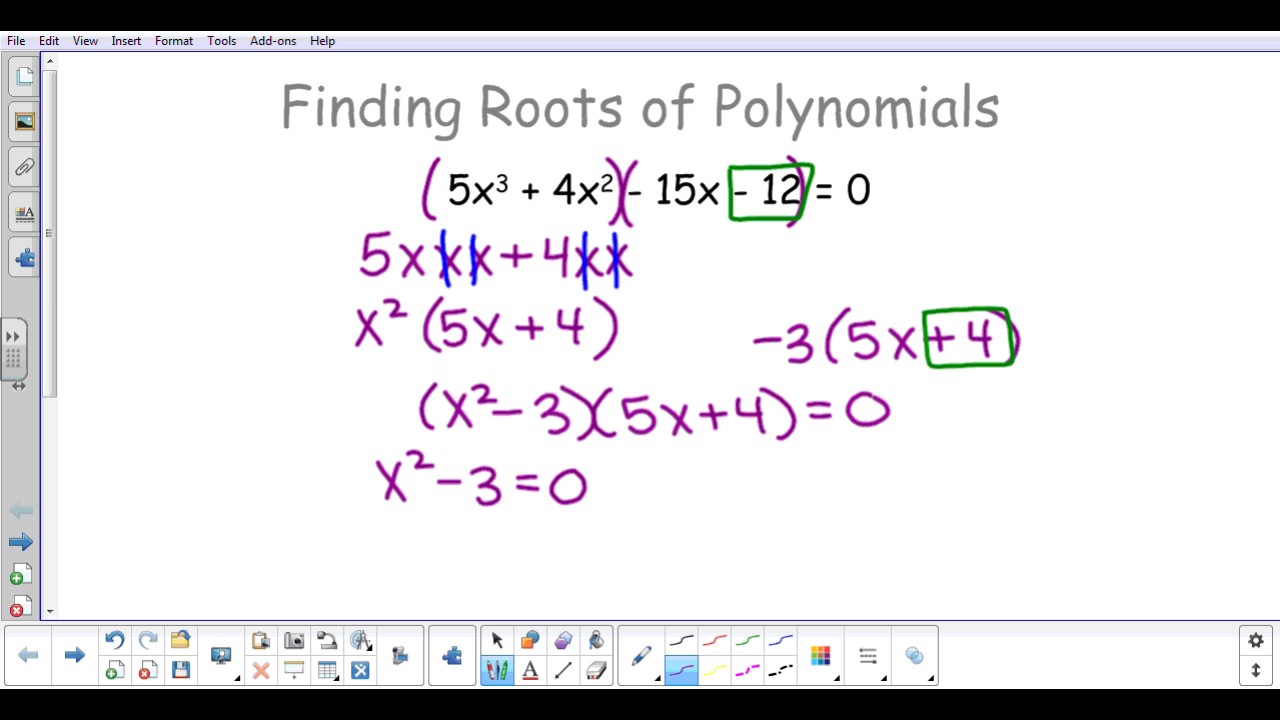
Finding Roots Of Polynomials YouTube
https://i.ytimg.com/vi/WbzaETJD6-Q/maxresdefault.jpg
We may be able to solve using basic algebra Example 2x 1 2x 1 is a linear polynomial The graph of y 2x 1 is a straight line It is linear so there is one root Use Algebra to solve A root is when y is zero 2x 1 0 Subtract 1 from both sides 2x 1 Divide both sides by 2 x 1 2 3x4 5x3 45x2 19x 30 0 2 8 2 2 8 2 3 x 4 5 x 3 45 x 2 19 x 30 0 First we ll graph the polynomial to see if we can find any real roots from the graph We can see roots at x 5 3 x 5 3 which means that x 5 x 5 and x 3 x 3 are both factors of this polynomial
The quadratic formula tells us that if we have a quadratic equation in the form ax squared plus bx plus c is equal to 0 so in standard form then the roots of this are x are equal to negative b plus or minus the square root of b squared minus 4ac all of that over 2a Fundamental connections for polynomial functions For a polynomial f and a real number k the following statements are equivalent x k is a root or solution of the equation f x 0 k is a zero of function f k 0 is an x intercept of the graph of y f x x k is a linear factor of f x

How To Factor Polynomials Step by Step Mashup Math
http://static1.squarespace.com/static/54905286e4b050812345644c/t/641dea92e6614b2dbc0eafb3/1679682194747/Banner-Image.jpg?format=1500w

Flexi Answers Which Algebraic Expression Is A Polynomial CK 12
https://www.ck12.org/flx/show/image/201502261424994918478166_c7b333e4c34c6747e56274f4f666a3f8-201502261424996250141776.png
is negative square root of 5 a polynomial - A root of a polynomial P z is a number z i such that P z i 0 The fundamental theorem of algebra states that a polynomial P z of degree n has n roots some of which may be degenerate For example the roots of the polynomial x 3 2x 2 x 2 x 2 x 1 x 1 1 are