integration formula product of two functions Integration by Parts is a special method of integration that is often useful when two functions are multiplied together but is also helpful in other ways You will see plenty of examples soon but first let us see the rule u v dx u v dx
Integration of uv formula is helpful for easily integrating the product of two functions This formula is expressed in two ways i uv dx u v dx u v dx dx ii u dv uv v du Integration by parts is the technique used to find the integral of the product of two types of functions The popular integration by parts formula is u dv uv v du Learn more about the derivation applications and examples of integration
integration formula product of two functions

integration formula product of two functions
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/integration-formula-1641294788.png

Integration Rules Integration Table Math Original
https://i2.wp.com/mathoriginal.com/wp-content/uploads/2020/11/integration-formulasT.png?fit=1536%2C1272&ssl=1

All Integration Formulas Complete List Of Integrals Cuemath
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/mahima-us-integration-02-1606905048.png
In calculus and more generally in mathematical analysis integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the Integration By Parts formula is used for integrating the product of two functions This method is used to find the integrals by reducing them into standard forms For example if we have to find the integration of x sin x then we need to use
Integrating by parts with v x and du dx e x we get xe x e x dx since e x dx e x xe x e x constant We can also sometimes use integration by parts when we want to integrate a function that cannot be split into the Then the integration by parts formula for the integral involving these two functions is udv uv vdu The advantage of using the integration by parts formula is that we can use it to exchange one integral for another
More picture related to integration formula product of two functions
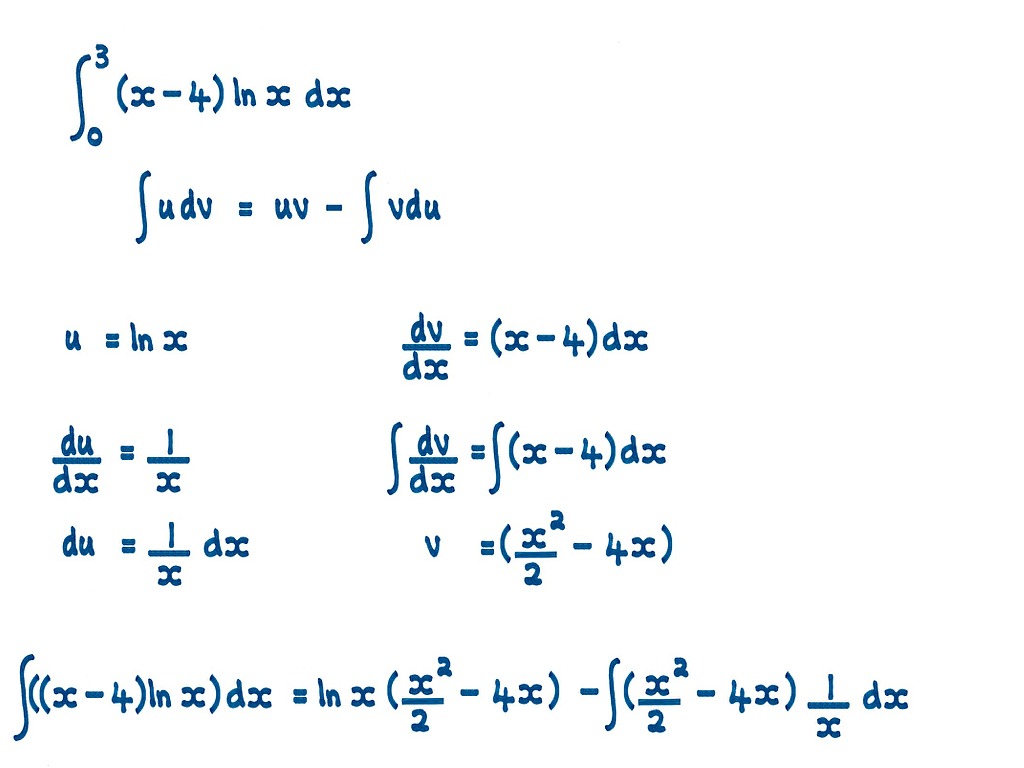
Formula Of Integration By Parts
https://showme0-9071.kxcdn.com/files/23268/pictures/thumbs/2463236/last_thumb1474690750.jpg

Integration By Parts the product Rule Of Integration YouTube
https://i.ytimg.com/vi/UUGAkkOl6uQ/maxresdefault.jpg

Integration Formula Examples List Of Integration Formulas
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/integration-formulas-1659702004.png
Integration by parts mc TY parts 2009 1 A special rule integration by parts is available for integrating products of two functions This unit derives and illustrates this rule with a Integration by parts or simply parts for short is often used to find the integrals of products of functions Note that u and v are both functions We need to choose one function to integrate and another one to differentiate as indicated
The integral product rule is a mathematical technique used to simplify integrals that involve a product of two functions It is a foundational tool of calculus allowing students to Integration by parts is a special integration technique that allows us to integrate functions that are products of two simpler functions In this article we ll show you how to apply integration by

Integration Formula For Trigonometry Function
https://trigidentities.net/wp-content/uploads/2020/06/integration-formulas-3-1583x2048.jpg

Integration By Parts Formula Derivation ILATE Rule Examples
https://images.collegedunia.com/public/image/_u_v_dx_u_v_dx_u_v_dx_dx_a78d995a70decc97104562ef48d1f37e.png
integration formula product of two functions - Then the integration by parts formula for the integral involving these two functions is udv uv vdu The advantage of using the integration by parts formula is that we can use it to exchange one integral for another