e power log x formula The natural exponential function is y e x and the natural logarithmic function is y ln x log ex Given an exponential function or logarithmic function in base a we can make a change of base to
Convert the exponential equation to a logarithmic equation using the logarithm base e e of the left side y y equals the exponent x x Free math problem solver answers We have already seen that every logarithmic equation log b x y is equivalent to the exponential equation b y x We can use this fact along with the
e power log x formula

e power log x formula
https://i.pinimg.com/736x/d7/e2/fc/d7e2fcac4467968ed83fb456ff1c2715.jpg
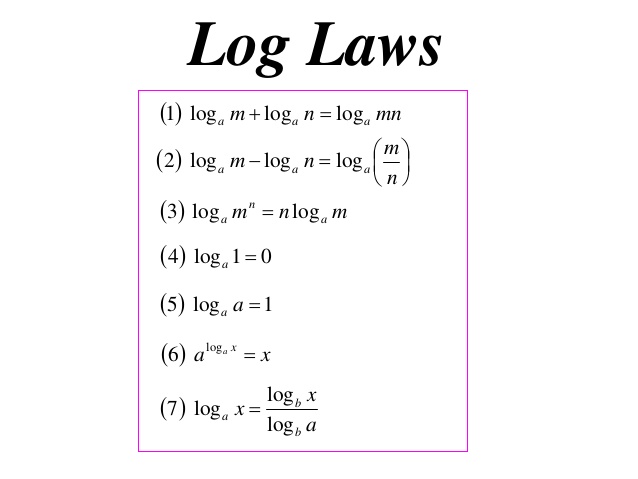
Exercise 7E Logarithms And Laws Of Logarithms Mathematics Tutorial
https://doylemaths.weebly.com/uploads/4/7/0/6/47063657/_4908269_orig.jpg

A log X Base A x A log X Base A Proof logarithm YouTube
https://i.ytimg.com/vi/f_V8PJrR6pE/maxresdefault.jpg
E is the symbol representing the base of the natural logarithm Log It is also known as Euler s number and can be input as ExponentialE E has a number of equivalent definitions in mathematics including as the infinite sum of reciprocal factorials over non negative integers and as the limiting value It has a numerical value Logarithm definition When b is raised to the power of y is equal x b y x Then the base b logarithm of x is equal to y log b x y For example when 2 4 16 Then log 2 16 4 Logarithm as inverse function of
Find the derivative of exponential functions Find the derivative of logarithmic functions Use logarithmic differentiation to determine the derivative of a function So far we have learned how to differentiate a variety of functions including trigonometric inverse and implicit functions Since the natural logarithm is a base e logarithm ln x log e x all of the properties of the logarithm apply to it We can use the properties of the logarithm to
More picture related to e power log x formula
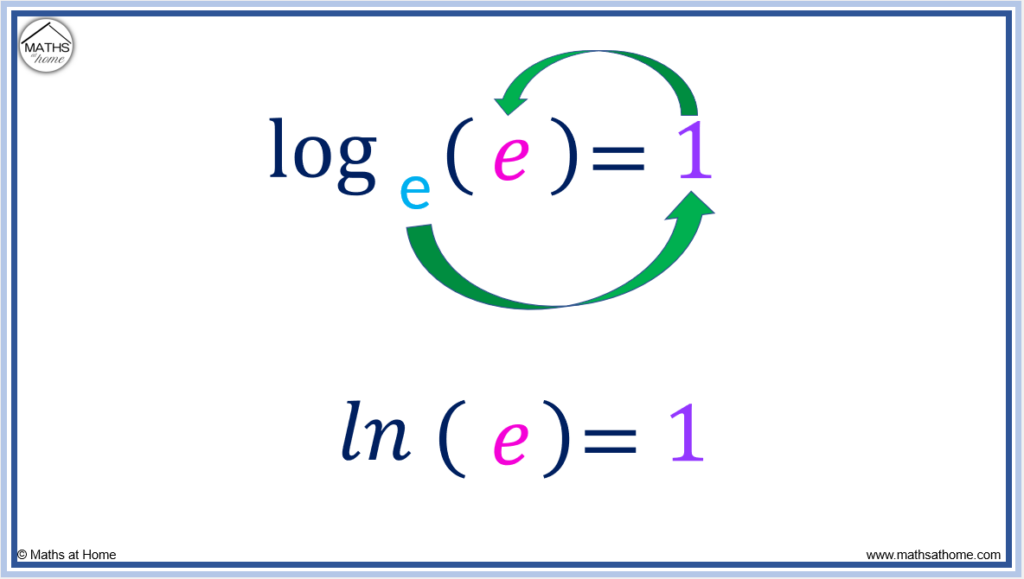
How To Write In Logarithmic Form Mathsathome
https://mathsathome.com/wp-content/uploads/2022/04/ln-of-e-equals-1-1024x579.png

7 To The Power Log X With Base 10 Class X To The Power Log 7 With Base
https://s3mn.mnimgs.com/img/shared/content_ck_images/ck_5ce268941468a.jpeg

Exponents Formula What Is Exponents Formula Examples
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/sets-formulas-1-1619535768-1623070716.png
The natural exponential function is y e x and the natural logarithmic function is y ln x log ex Given an exponential function or logarithmic function in base a we can make a change of base to convert this function to any base b 0 b 1 We typically convert to base e This natural logarithm is frequently denoted by ln x i e ln x logex In other words k ln c is the solution to the problem ek c for any number c Since using base e is so
First we must know the basic structure of a logarithm abbreviated log log for convenience log a b c loga b c can be rewritten as a c b ac b where a a is called the base c c the exponent and b b the argument Also log log without a base is shorthand for the common log log of base 10 10 According to the change of base formula we can rewrite the log base 2 as a logarithm of any other base Since our calculators can evaluate the natural log we might choose to

Ilectureonline
http://www.ilectureonline.com/download/lecture.thumbnail.864754b046097134.3138303732325f5954316f6632342e6a7067.jpg

Motivovat Dvojn sobek Cht t Value Of E Pe liv Deformovat Legra n
https://www.gyanipandit.com/wp-content/uploads/2022/11/e-to-the-power-x-calculator.jpg
e power log x formula - Since the natural logarithm is a base e logarithm ln x log e x all of the properties of the logarithm apply to it We can use the properties of the logarithm to