cosine rule

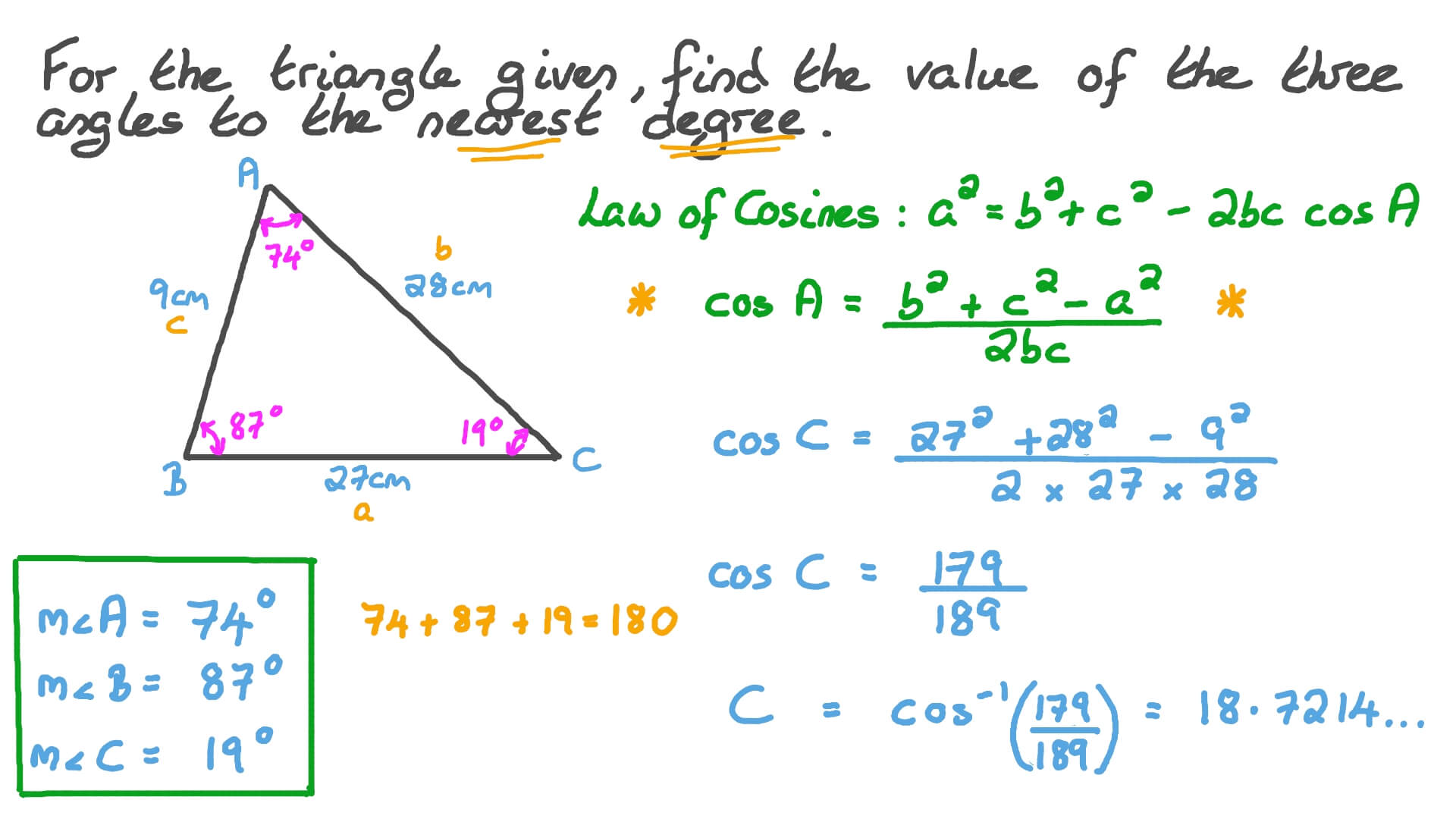
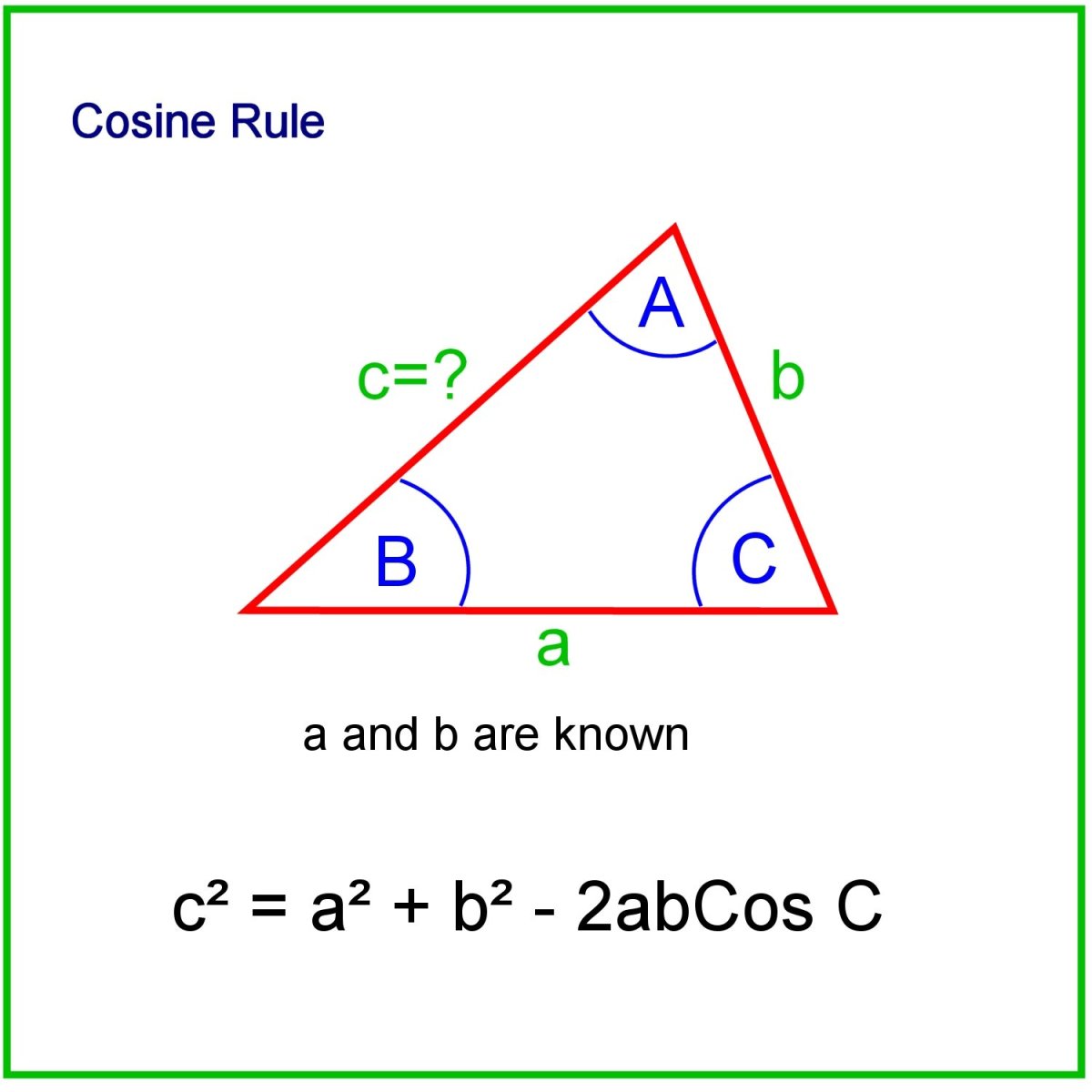
cosine rule The Law of Cosines For any triangle a b and c are sides C is the angle opposite side c the Law of Cosines also called the Cosine Rule says c 2 a 2 b 2 2ab cos C It helps us solve some triangles Let s see how to use it Example How long is side c We know angle C 37 and sides a 8 and b 11

The law of cosines generalizes the Pythagorean theorem which holds only for right triangles if is a right angle then and the law of cosines reduces to The law of cosines is useful for solving a triangle when all three sides or two sides and their included angle are given The cosine rule also known as the law of cosines relates all 3 sides of a triangle with an angle of a triangle It is most useful for solving for missing information in a triangle For example if all three sides of the triangle are known the cosine rule allows one to find any of the angle measures

cosine rule

cosine rule
http://4.bp.blogspot.com/-3BoCaAVNMVo/VPXChgl3pjI/AAAAAAAABq4/iqMcajtf7aU/s1600/Cosine%2BRule%2BFormula.PNG

Question Video Applying The Cosine Rule To Solve Triangles Nagwa
https://media.nagwa.com/105196860191/en/thumbnail_l.jpeg

The Cosine Rule Teaching Resources
https://d1e4pidl3fu268.cloudfront.net/35b57af3-19da-4883-b9d0-123918f7510b/ScreenTES.png

The cosine rule or the law of cosines is a formula which can be used to calculate the missing sides of a triangle or to find a missing angle To do this we need to know the two arrangements of the formula and what each variable represents Take a Law of cosines signifies the relation between the lengths of sides of a triangle with respect to the cosine of its angle It is also called the cosine rule If ABC is a triangle then as per the statement of cosine law we have a 2 b 2 c 2 2bc cos where a b and c are the sides of triangle and is the angle between sides b and c

The law of cosine is also known as the cosine rule This law is useful to find the missing information in any triangle For example if you know the lengths of two sides of a triangle and an angle included between them this rule helps to find the third side of the triangle Want to learn more about the law of cosines Check out this video Practice set 1 Solving triangles using the law of sines This law is useful for finding a missing angle when given an angle and two sides or for finding a missing side when given two angles and one side Example 1 Finding a missing side Let s find A C in the following triangle

More picture related to cosine rule

Question Video Using The Cosine Rule To Find The Measures Of A
https://media.nagwa.com/108148710289/en/thumbnail_l.jpeg

MEDIAN Don Steward Mathematics Teaching cosine Rule
https://1.bp.blogspot.com/-42Dpfok296I/WXO2tUY7LVI/AAAAAAAAVhI/lukaqGeuPhkI6yCnNo9V0582pmpN77zEwCLcBGAs/s1600/Picture7.png

How To Calculate The Missing Sides And Angles Of Triangles Owlcation
https://images.saymedia-content.com/.image/t_share/MTc0NjQ1NjQwNzA5NjEzMzI3/everything-about-triangles-and-more-isosceles-equilateral-scalene-pythagoras-sine-and-cosine.jpg

You can ONLY use the Pythagorean Theorem when dealing with a right triangle The law of cosines allows us to find angle or side length measurements for triangles other than right triangles The third side in the example given would ONLY 15 if the angle between the two sides was 90 degrees Cosumnes River College Math 370 Precalculus 11 Applications of Trigonometry 11 3 The Law of Cosines

[desc-10] [desc-11]

Question Video Using The Cosine Rule To Find The Side Lengths Of An
https://media.nagwa.com/139120216703/en/thumbnail_l.jpeg

Cosine Rule When To Use Them YouTube
https://i.ytimg.com/vi/_S-suaxdHtc/maxresdefault.jpg

cosine rule - [desc-14]