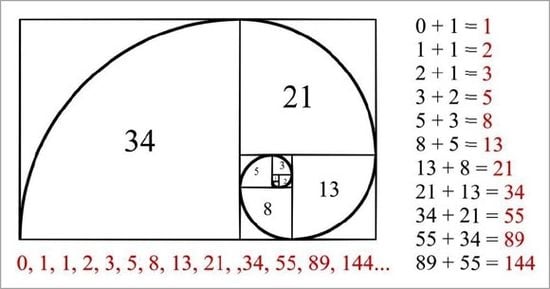
2 3 5 8 13 sequence A tiling with squares whose side lengths are successive Fibonacci numbers 1 1 2 3 5 8 13 and 21 In mathematics the Fibonacci sequence is a sequence in which each number is the sum of the two preceding ones Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers commonly denoted Fn
Fibonacci sequence the sequence of numbers 1 1 2 3 5 8 13 21 each of which after the second is the sum of the two previous numbers that is the n th Fibonacci number Fn Fn 1 Fn 2 The sequence was noted by the medieval Italian mathematician Fibonacci Leonardo Pisano in his Liber abaci 1202 Book of the And while in other instances this would cause the sequence to repeat itself after the third term the numbers of the Fibonacci sequence never repeat The next terms would be begin split a 3 1 1 2 a 4 2 1 3 a 5 3 2 5 a 6 5 3 8 a 7 8 5 13 end split a3a4a5a6a7 1 1 2 2 1 3 3 2 5 5 3 8 8 5 13
2 3 5 8 13 sequence
2 3 5 8 13 sequence
https://thumbor.guiame.com.br/unsafe/smart/https://media.guiame.com.br/archives/2022/06/20/712672638-assisnatura-de-deus1.jpg
Ex Springer Hannawald Wird Langsam Zeit F r Tournee Sieger
https://img.wochenblatt.de/ezplatform/images/6/2/3/5/26425326-4-ger-DE/urn:newsml:dpa.com:20090101:211222-99-472661-v2-s2048.jpeg
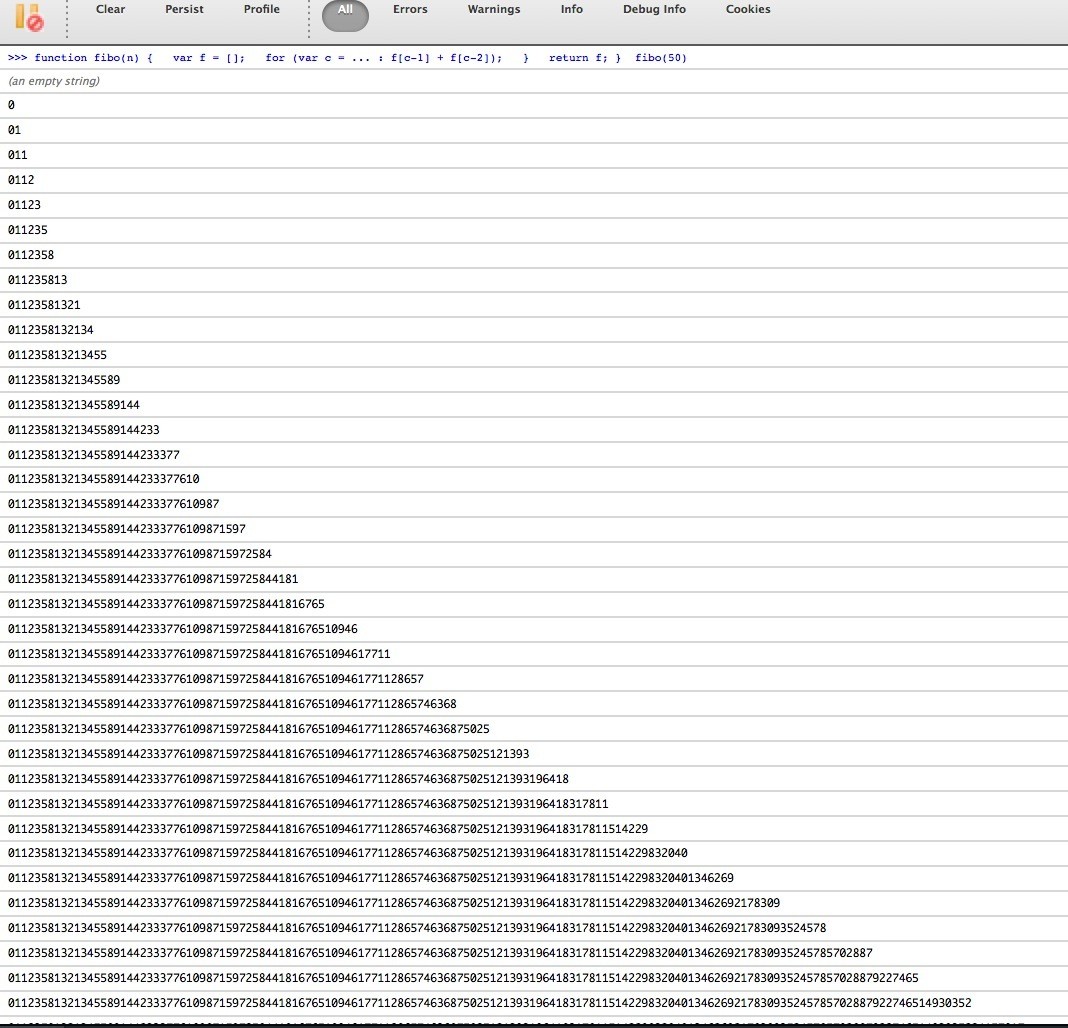
0 1 1 2 3 5 8 13 21 34 N js FreeSpider
https://images0.cnblogs.com/blog/104965/201310/18202037-0fc9a64e24964e9dbbffe2661db8cdac.jpg
Free sequence calculator step by step solutions to help identify the sequence and find the nth term of arithmetic and geometric sequence types Fibonacci Number Patterns Go Figure Math Print friendly version Here for reference is the Fibonacci Sequence 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 We already know that you get the next term in the sequence by adding the two terms before it But let s explore this sequence a little further
The Fibonacci Sequence is given as 0 1 1 2 3 5 8 13 21 Here we obtain the third term 1 by adding the first and second term 0 1 1 Similarly we obtain 2 by adding the second and third term 1 1 2 So the term after 21 will be the sum of 13 and 21 i e 13 21 34 Therefore the next term in the sequence is 34 So 1 1 2 1 2 3 2 3 5 and so on This gives you a sequence that looks like 1 1 2 3 5 8 13 21 34 55 etc But what makes this sequence so special and
More picture related to 2 3 5 8 13 sequence
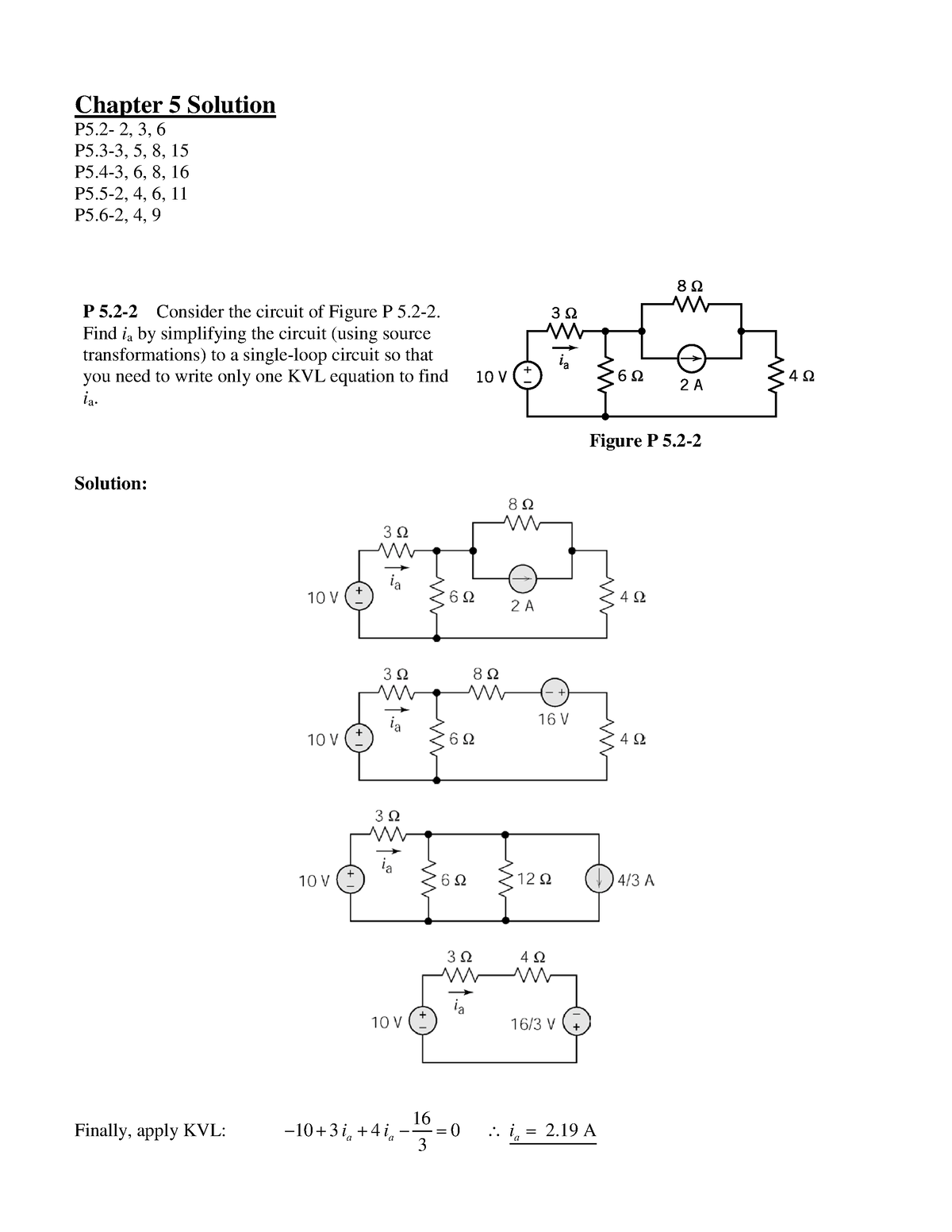
Chapter 5 Homework Solution Chapter 5 Solution P5 2 3 6 P5 3 5 8
https://d20ohkaloyme4g.cloudfront.net/img/document_thumbnails/f0155ad3c1eb345000627168664e0893/thumb_1200_1553.png
The Fibonacci Sequence YouTube
https://i.ytimg.com/vi/ZC-d4dKTyKw/maxresdefault.jpg
C mo Convertir Millas A Kil metros Con Un Truco Matem tico De Fibonacci
http://www.wikihow.com/images/3/3c/Make-Math-Easy-Step-6.jpg
The pattern 1 1 2 3 5 8 13 etc is the Fibonacci sequence It shows up all over nature But what s the full explanation behind it The normal multi armed spiral galaxy IC Some examples of an arithmetic sequence include 3 5 7 9 11 13 15 17 19 21 6 3 0 3 6 9 12 15 50 50 1 50 2 50 3 50 4 50 5 Can you find the common difference of each of these sequences Hint try
Definition a n a 1 f n 1 example 1 3 5 7 9 11 13 Geometric Sequence Calculator definition a n a r n 1 example 1 2 4 8 16 32 64 128 Fibonacci Sequence Calculator definition a 0 0 a 1 1 a n a n 1 a n 2 example 0 1 1 2 3 5 8 13 21 34 55 Solution Compute the next number of the series Given 1 1 2 3 5 8 13 In the given series we got the third number by adding the first and second numbers 1 1 2 We got the fourth number by adding the second and third numbers 2 3 5 Similarly 3 5 8 5 8 13 Thus the next number of the series will be 8 13 21
2 5 2 3 5 4 3 1 5 2 3 Brainly in
https://hi-static.z-dn.net/files/d56/5335f1006026f61668c9490678df2e31.jpg
The Fibonacci Numbers Are The Sums Of The shallow Diagonals shown In
https://i.pinimg.com/originals/d2/7b/37/d27b37c554faec7a8aef16dc6eebde87.png
2 3 5 8 13 sequence - 0 1 1 2 3 5 8 13 21 34 The Fibonacci Sequence is found by adding the two numbers before it together The 2 is found by adding the two numbers before it 1 1