1 3 9 27 sequence rule 1 1 3 3 9 9 27 27 81 81 243 243 This is a geometric sequence since there is a common ratio between each term In this case multiplying the previous term in the sequence by 3 3
Explanation The given sequence is 1 3 9 27 First term a1 1 and common ratio r 27 9 9 3 3 1 3 Now a1 1 a2 3 a3 9 a4 27 So the Free sequence calculator step by step solutions to help identify the sequence and find the nth term of arithmetic and geometric sequence types
1 3 9 27 sequence rule

1 3 9 27 sequence rule
https://i.ytimg.com/vi/_TBxyLMBTC0/maxresdefault.jpg

Find The Next Three Terms In Each Sequence Then Write The Rule For
https://ph-static.z-dn.net/files/d42/b8a450d225bee2468b2e8b16cc3e74f2.jpg

What I Know Let Us Find Out How Much You Already Know About The Content
https://ph-static.z-dn.net/files/d26/3292298c925f668a68801bac80801622.jpg
What should be the next number in the following series 3 9 27 81 243 Solution Given the series 3 9 27 81 243 is in geometric progression First term a 3 Common ratio r 9 3 1 can be rewritten as 3 0 3 can be rewritten as 3 1 9 can be rewritten as 3 2 So each term 1st 2nd 3rd etc can be written as 3 n 1 where n is the place of the term in the
Learn how to solve 1 3 9 27 Tiger Algebra s step by step solution shows you how to find the common ratio sum general form and nth term of a geometric sequence To find a missing number in a Sequence first we must have a Rule Sequence A Sequence is a set of things usually numbers that are in order Each number in the sequence is called a term
More picture related to 1 3 9 27 sequence rule

Incredible The Arithmetic Sequence References Deb Moran s Multiplying
https://i2.wp.com/www.flexiprep.com/NCERT-Exercise-Solutions/Mathematics/Class-10/posts/Ch-5-Arithmetic-Progression-Exercise-5-2-Solutions-Part-3/Example-of-find-the-term-of-arithmetic-sequence.png

15 Find The Perimeter Of Thisrectangle 13 12 Brainly in
https://hi-static.z-dn.net/files/d5e/9ec5595322dbaeabab0d6363b6c41663.jpg

FLIPPING OVER FLIPGRID QR CODES
http://www.bunheadwithducttape.com/uploads/1/3/9/7/1397063/slide1_orig.jpg
Use the geometric sequence of numbers 1 3 9 27 to find the following a What is r the ratio between 2 consecutive terms Answer r 3 Show work in this space The geometric sequence is sometimes called the geometric progression or GP for short For example the sequence 1 3 9 27 81 is a geometric sequence Note that after the first term the next term is obtained by multiplying the
Explanation The 2nd term is 3 the 3rd 9 32 the 4th 27 33 To get to the n th term we will have to multiply n 1 times by 3 Or tn 3n 1 Watch out Usually the first term 1 1 3 3 9 9 27 27 This is a geometric sequence since there is a common ratio between each term In this case multiplying the previous term in the sequence by 3 3 gives the next
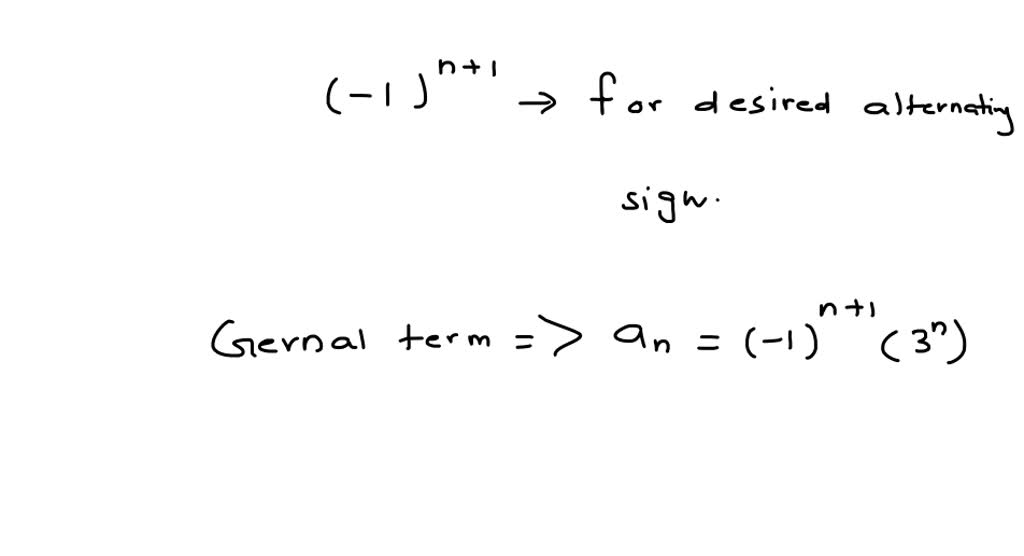
SOLVED Write Each Series Using Summation Notation 3 9 27 81
https://cdn.numerade.com/previews/f29eea22-246d-4672-b8bd-76b3fec3c149_large.jpg

Find The 2017th Term Of The Sequence Of 13 7 1 5 Brainly ph
https://ph-static.z-dn.net/files/dd9/fedd53433e3ec914009db4e71e6184ff.jpg
1 3 9 27 sequence rule - A geometric sequence is a sequence in which the ratio of two consecutive terms is a fixed ratio Given Geometric sequence 1 3 9 27 The ratio of second and first term 3 1