1 2ka 2 1 2mv 2

1 2ka 2 1 2mv 2 Total energy E 1 2 mv 2 1 2 kx 2 At any position x E 1 2 mv x 2 1 2 kx 2 At the extreme position i e at x A the block has only potential energy so E 1 2 kA 2 At the equilibrium position at x 0 the block has only kinetic energy so E 1 2 mv max 2 Now we know v max A so at x 0 E 1 2 m 2 A 2

1 PE Max 2 KE Max 3 Acceleration Max 4 Acceleration Min PE at C equals KE at B Ex Mass M is attached to a spring with a spring constant k If the maximum displacement of a mass M from its equilibrium position is A find the velocity of the mass at B is PE max KE 1 2kA 2 1 2mv 2 Velocity Amplitude Direct 1 Answer a purely kinetic At the mean position the velocity of the particle in S H M is maximum and displacement is minimum that is x 0 Therefore P E 1 2 K x 2 0 and K E 1 2 k a 2 x 2 1 2 k a 2 o 2 1 2 ka 2 Thus the total energy in simple harmonic motion is purely kinetic

1 2ka 2 1 2mv 2

1 2ka 2 1 2mv 2
https://traktor.com.pl/img/cms/!1Przyczepa wywrotka 7CX-1(E)n 200x100x40 cm (5).jpg

Check The Correctness Of The 1 2mv 2 mgh dimension Brainly in
https://hi-static.z-dn.net/files/d38/8dc3e74dd5b1c874f0b822ff57ac600c.jpg

Derive K 1 2 Mv 2 And Get 100 Points Brainly in
https://hi-static.z-dn.net/files/d9d/b439095d6abe3de113e78f32e1ce6d90.jpg

I understand that both KE and U are 1 2 kA 2 So how is it that the two combine is also equal to 1 2kA 2Not sure if I m missing something but I m a little confused KE 1 2 mv 2 and v Acos t So KE 1 2 m 2 A 2 cos 2 t But k m 2 Hence KE 1 2 kA 2 cos 2 t 1 PE 1 2 kx 2 and x Asin t So PE 1 2 How do you solve for m in the equation 1 2 mv2 1 2 kx2 Physics 1 Answer G Ozdilek Apr 17 2017 If v x m will be solved m k Explanation Since 0 5 or 1 2 is on both sides you can get rid of it easily Now you have mv2 kx2 In other words m k if v2 x2 or v x Answer link

The kinetic energy is maximum and equal to K frac 1 2 mv 2 frac 1 2 mA 2 omega 2 frac 1 2 kA 2 At this point the force on the block is zero but momentum carries the block and it The frequency f 1 T Potential and Kinetic Energy Maximum potential energy PE max 1 2 kA 2 where k is spring constant A is ampilude or maximumly stretched displacement Maximum kinetic energy KE max 1 2 mv 2 max 1 2 kA 2 where v is maximum velocity achieved at equilibrium point Potential energy at displacement x PE

More picture related to 1 2ka 2 1 2mv 2

Dynacord Powermate 2ka 2 700w
https://media.pazar3.mk/Image/56736075fa6742e2966052d40fb2f94b/20170918/false/false/1280/960/dynacord-powermate-2ka-2-700w.jpeg

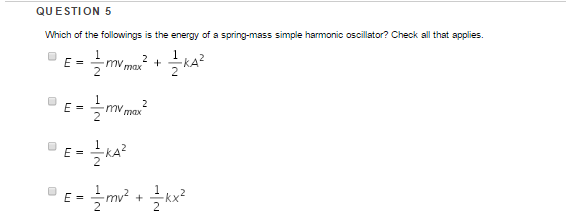
Solved Which Of The Followings Is The Energy Of A Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/d27/d2771220-3d31-4ec7-bcb8-a31743a77cb3/phpKsaFzs.png

Girafe On Twitter TinyJohn OtraPendeja Yo Adopt A Mi Perra En Ese
https://pbs.twimg.com/media/EWEwrM4WoAAVtq2.jpg:large

Google Classroom Review the key concepts equations and skills for kinetic energy Understand how kinetic energy can t be negative but the change in kinetic energy can be negative Key terms Equations Why do we use only the magnitude of the velocity Common mistakes and misconceptions 1 2kx 2 1 2mv 2 constant is 1 2kx 2 and 1 2kA 2 the same thing only when x is at its maximum or minimum value how can we set PE and KE equal to each other for a spring 1 2kA 2 1 2m Vmax 2 what is Vmax equal to

What is the maximum potential energy in simple harmonic motion Group of answer choices E 1 2mv 2 E 1 2KA 2 E 1 2Kx 2 E 1 2m max v 2 This problem has been solved You ll get a detailed solution from a subject matter expert that helps you learn core concepts See Answer Question What is the maximum potential energy in simple Since this is the work done on the object by the force it is equal to the energy transferred to the kinetic energy store of the object In other words it is the energy the object has gained because it is moving its kinetic energy no less Ek mv2

SOLVED Harmonic And Anharmonic Oscillators 1 Choose X 0 When The
https://cdn.numerade.com/ask_previews/58c96ad2-f05e-498d-a4e8-830d022f7dea_large.jpg

1 2mv 2 1 2kx 2 1 2kA 2 Yahoo
https://chie-pctr.c.yimg.jp/dk/iwiz-chie/que-11235078621?w=200&h=200&up=0

1 2ka 2 1 2mv 2 - I understand that both KE and U are 1 2 kA 2 So how is it that the two combine is also equal to 1 2kA 2Not sure if I m missing something but I m a little confused KE 1 2 mv 2 and v Acos t So KE 1 2 m 2 A 2 cos 2 t But k m 2 Hence KE 1 2 kA 2 cos 2 t 1 PE 1 2 kx 2 and x Asin t So PE 1 2