x 3 x 2 1 0 by bisection method Algorithm for the bisection method The steps to apply the bisection method to find the root of the equation f x 0 are Choose x l and x u as two guesses for the root such that f x l f x u 0 or in other words f x changes sign between x l and x u
Find the root of the following polynomial function using the bisection method x 3 4 Solution Let f x x 3 4 f 0 0 4 4 f 1 1 4 3 f 2 8 4 4 the root lies in 1 2 First iteration x 1 1 2 2 1 5 Now f x 1 1 5 3 4 0 625 Then f x 1 f 2 0 Thus the root lies This is a calculator that finds a function root using the bisection method or interval halving method A brief method description can be found below the calculator Bisection method Function Initial value x0 Initial value x1 Desired tolerance Tolerance type Endpoint convergence Function convergence Calculation precision
x 3 x 2 1 0 by bisection method

x 3 x 2 1 0 by bisection method
https://i.ytimg.com/vi/yqSO_De2058/maxresdefault.jpg

Bisection Method Made Easy YouTube
https://i.ytimg.com/vi/wordn57_Br8/maxresdefault.jpg

Questions Solve By Bisection Method X 3 x 1 0 Bolzano Method
https://i.ytimg.com/vi/5GAl6Isjvbk/maxresdefault.jpg
Figure 1 f x x3 2x2 3x 1 1 Note f 0 f 2 2 2 4 0 so f indeed has a root in 0 2 by IVT Set p 1 1 and notice f 0 f 1 2 1 0 so choose a 2 b 2 1 2 2 Set p 2 1 2 2 3 2 and notice f a 2 f p 2 1 9 4 2 1 4 0 so choose a 3 b 3 1 3 2 3 Set p 3 1 3 2 2 5 4 Example 1 Consider finding the root of f x x2 3 Let step 0 01 abs 0 01 and start with the interval 1 2 Table 1 Bisection method applied to f x x2 3 Thus with the seventh iteration we note that the final interval 1 7266 1 7344 has a width less than 0 01 and f 1 7344 0 01 and therefore we chose b 1
The value of x3 x 3 is then chosen as either the midpoint of x0 x 0 and x2 x 2 or as the midpoint of x2 x 2 and x1 x 1 depending on whether x0 x 0 and x2 x 2 bracket the root or x2 x 2 and x1 x 1 bracket the root The root therefore stays bracketed at Approximate the root of f x x 3 3 with the bisection method starting with the interval 1 2 and use step 0 1 and abs 0 1 Answer 1 4375 Question 2 Approximate the root of f x x 2 10 with the bisection method starting with the interval 3 4 and use step 0 1 and abs 0 1
More picture related to x 3 x 2 1 0 by bisection method

Find The Real Root Of Equation X 3 3x 5 0 By Newton Raphson Method
https://i.ytimg.com/vi/OeabACE1Srk/maxresdefault.jpg

Bisection Method Example Paymentsxaser
https://paymentsxaser.weebly.com/uploads/1/3/3/5/133586862/184850005_orig.jpg

A Use Bisection Method To Obtain First Positive Root Of The Following
https://cdn.eduncle.com/library/scoop-files/2020/8/image_1598620028890.jpg
Your first reaction might be to say Hey wait this function isn t continuous or differentiable at x 0 x 0 However x 0 x 0 isn t in the interval between 1 1 and 4 4 so this method can be used f 1 frac 2 3 quad f 4 frac 1 12 f 1 32 f 4 121 Now we bisect and repeat Explore math with our beautiful free online graphing calculator Graph functions plot points visualize algebraic equations add sliders animate graphs and more
Figure 1 Bisection Method INPUT endpoints a b The results of the problem f x x 3 4x 2 10 0 is obtained by using the Bisection Method The iteration number and the p value obtained after this iteration are provided as follows Iteration Number P n 1 1 5 2 1 25 3 1 375 Bisection Method The Bisection Method Algorithm C Fortran Scilab Bisection method is a technique to find the roots of algebraic and transcendental equations of the form f x 0 f x 0 such as xex 1 0 x e x 1 0
Solved 2 1 Find The Real Root Of The Equation X3 3x Chegg
https://media.cheggcdn.com/media/892/8922ea5e-8861-456c-9200-60071219cf35/phptqZcs5
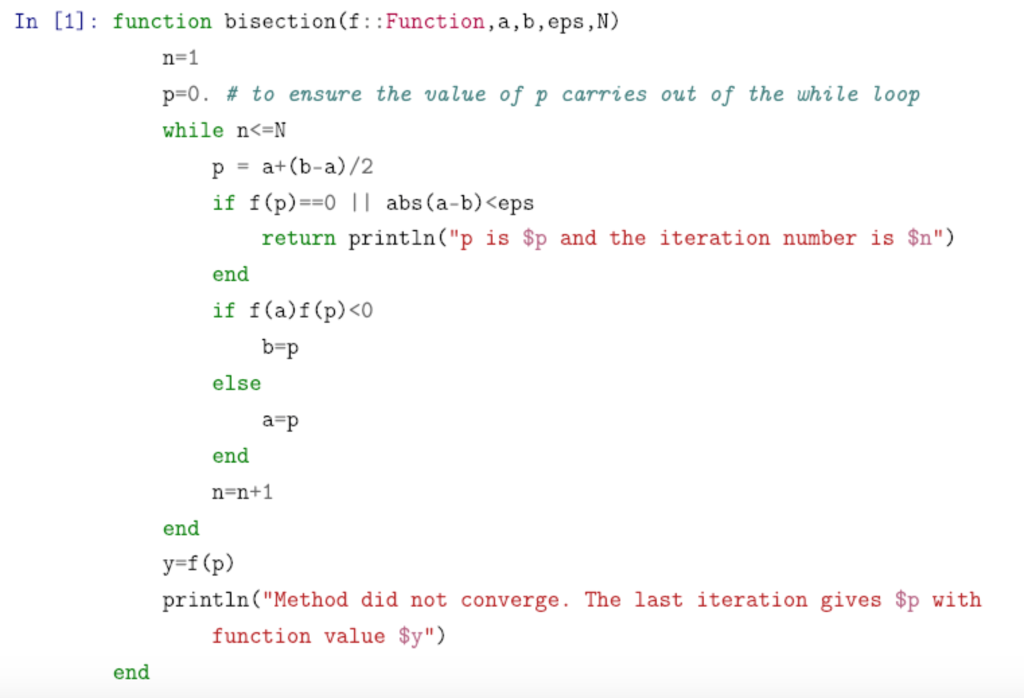
Exercise 2 2 1 Find The Root Of F x 4z2 10 Using Chegg
https://media.cheggcdn.com/media/e5e/e5e19ce5-ef90-4ec4-817f-d62928b3b3c3/phpF955vn.png
x 3 x 2 1 0 by bisection method - In mathematics the bisection method is a root finding method that applies to any continuous function for which one knows two values with opposite signs The method consists of repeatedly bisecting the interval defined by these values and then selecting the subinterval in which the function changes sign and therefore must contain a root
