x 3 mod 5 solution 1 mod 1 0 as mod 1 is always 0 1 mod 2 1 1 mod 3 1 5 mod 2 1 5 mod 3 2 6 mod 3 0 7 mod 3 1 10 mod 3 1 18 mod 3 0 100 mod 3 1 100 mod 7 2 If you don t see the one you want to find here don t hesitate to use our modulo calculator
Multiplying both sides with 3 we will get 6X 1 3 mod 5 X 1 3 mod 5 X 1 3 Again using the above relation 5X 2 1 mod 7 15X 2 3 mod 7 X 2 3 mod 7 X 2 3 Hence the unique solution of x will be X M 1 X 1 a 1 M 2 X 2 a 2 X 7 3 3 5 5 3 138 X 138 mod 35 X The Chinese Remainder Theorem CRT tells us that since 3 5 and 7 are coprime in pairs then there is a unique solution modulo 3 x 5 x 7 105 The solution is x 23 You can check that by noting that the relations 23 7 x 3 2 2 mod 3 23 4 x 5 3 3 mod 5 23 3 x 7 2 2 mod 7 are all satisfied for
x 3 mod 5 solution
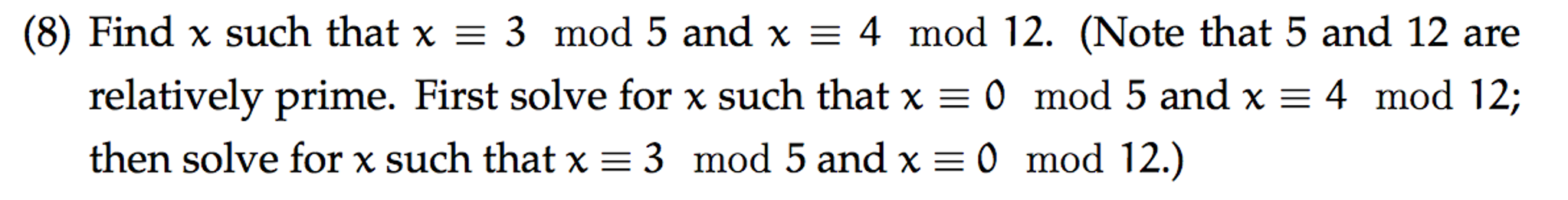
x 3 mod 5 solution
https://d2vlcm61l7u1fs.cloudfront.net/media/5e1/5e1f8887-9544-4251-991f-340ad751df88/phpU6FcOA.png

Dead Or Alive Xtreme 3 Ayane Hitomi Kokoro Helena Kasumi Momiji
https://1.bp.blogspot.com/-PLRZ0WSpWKQ/XYAvidFO9jI/AAAAAAAAYk8/dXMTvBo618gIJT6YUUScbwLwvT0m5SrMgCLcBGAsYHQ/s1600/Captura%2Bde%2Bpantalla%2B%2528501%2529.png

Answered 1 Solve The Following Linear Bartleby
https://content.bartleby.com/qna-images/question/66c7b497-dac7-4855-b923-2e60bbc73063/c4b3e527-b83d-45b5-aad4-8959af65571f/tkqqpe.jpeg
X 3 mod 5 X 5 mod 7 The common solution is 1 X 33 mod 35 2 X 31 mod 5 3 X 27 mod 35 4 X 28 mod 35 Here is the math to illustrate how to get 3 mod 5 using our Modulo Method 3 5 0 6 0 5 0 3 0 3 Thus the answer to What is 3 mod 5 is 3 Modulus Method To find 3 mod 5 using the Modulus Method we first find the highest multiple of the Divisor 5 that is equal to or less than the Dividend 3 Then we subtract the
1 For a you are expected to try 0 1 2 3 4 0 1 2 3 4 and conclude that x 4 mod 5 x 4 mod 5 is the unique solution Similarly for b you are expected to try 0 1 10 0 1 10 and conclude that x 5 mod 11 x 5 mod 11 is the unique solution Obviously for c you use the CRT almagest Modulo Method First need to divide the Dividend by the Divisor 3 5 0 60 Next we take the Whole part of the Quotient 0 and multiply that by the Divisor 5 0 x 5 0 And finally we take the answer in the second step and subtract it from the Dividend to get the answer to 3 mod 5 3 0 3 As you can see the answer to 3 mod 5 is 3
More picture related to x 3 mod 5 solution
Solved Solve 3x 3 2 mod 5 Write Your Answer As A Congruence
https://www.coursehero.com/qa/attachment/30318364/

Solved Find All Integers X So That X 1 Mod 3 X 3 Mod 5 X Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/0f3/0f309305-772b-4911-951a-9c56e9f34701/php350lYY.png

Number Theory Chinese Remainder Theorem Example 4 YouTube
https://i.ytimg.com/vi/XoTEKjS61kI/maxresdefault.jpg
Example 1 Find x such that 3x 7 mod 10 Solution Based on our previous work we know that 3 has a multiplicative inverse modulo 10 namely 3 10 1 Moreover 10 4 so the inverse of 3 modulo 10 is 33 Hence multiplying both sides of the above equation by 7 we obtain 3x 7 mod 10 7 3x 7 7 mod 10 x 49 9 mod Math Modulo Calculator a mod b dividend a modulus divisor b Answer 5 mod 2 1 Proof Divide a by b to find the remainder 5 2 2 R1 Confirm the answer satisfies the equation Quotient Divisor Remainder Dividend 2 2 1 5 Share this Answer Link help Paste this link in email text
In this section we discuss the solution of a system of congruences having different moduli An example of this kind of systems is the following find a number that leaves a remainder of 1 when divided by 2 a remainder of 2 when divided by three and a remainder of 3 when divided by 5 4 Answers Sorted by 2 x 2 mod 3 5x 10 mod 15 x 2 mod 3 5 x 10 mod 15 x 3 mod 5 3x 9 mod 15 x 3 mod 5 3 x 9 mod 15 Subtracting 2x 1 mod 15 x 8 mod 15 2 x 1 mod 15 x 8 mod 15 Share Cite
Solved Use The Chinese Remainder Theorem To Solve The System Of
https://www.coursehero.com/qa/attachment/13194456/

Wkst Law Of Sines Area Of Triangle
https://s3.studylib.net/store/data/008797837_1-bbbf826988bb42293c5dbc589b4cab94-768x994.png
x 3 mod 5 solution - The following is a general construction to find a solution to a system of congruences using the Chinese remainder theorem Compute N n 1 times n 2 times cdots times n k N n1 n2 nk For each i 1 2 ldots k i 1 2 k compute y i frac N n i n 1n 2 cdots n i 1 n i 1 cdots n k yi ni