what is the formula for sum of arithmetic sequence Arithmetic Series sum latex large 2 4 6 8 10 latex Notice that in a sequence we list the terms separated by commas while in a series the terms are added as indicated by the plus symbols Therefore an arithmetic seriesis simply the sum of the terms of an arithmetic sequence
Has a 1 the first term d 3 the common difference between terms And we get a a d a 2d a 3d 1 1 3 1 2 3 1 3 3 1 4 7 10 Rule We can write an Arithmetic Sequence as a rule xn a d n 1 We use n 1 because d For the formulas of an arithmetic sequence it is important to know the 1st term of the sequence the number of terms and the common difference Now Where a n n th term that has to be found a 1 1 st term in the sequence n Number of terms d Common difference S n Sum of n terms
what is the formula for sum of arithmetic sequence

what is the formula for sum of arithmetic sequence
https://i.ytimg.com/vi/6m6tkQ4lojU/maxresdefault.jpg

Sum Of The First N Terms Of An Arithmetic Progression A Plus Topper
https://i2.wp.com/www.aplustopper.com/wp-content/uploads/2016/08/Arithematic-progression-formula.jpg?resize=1299%2C1308&ssl=1
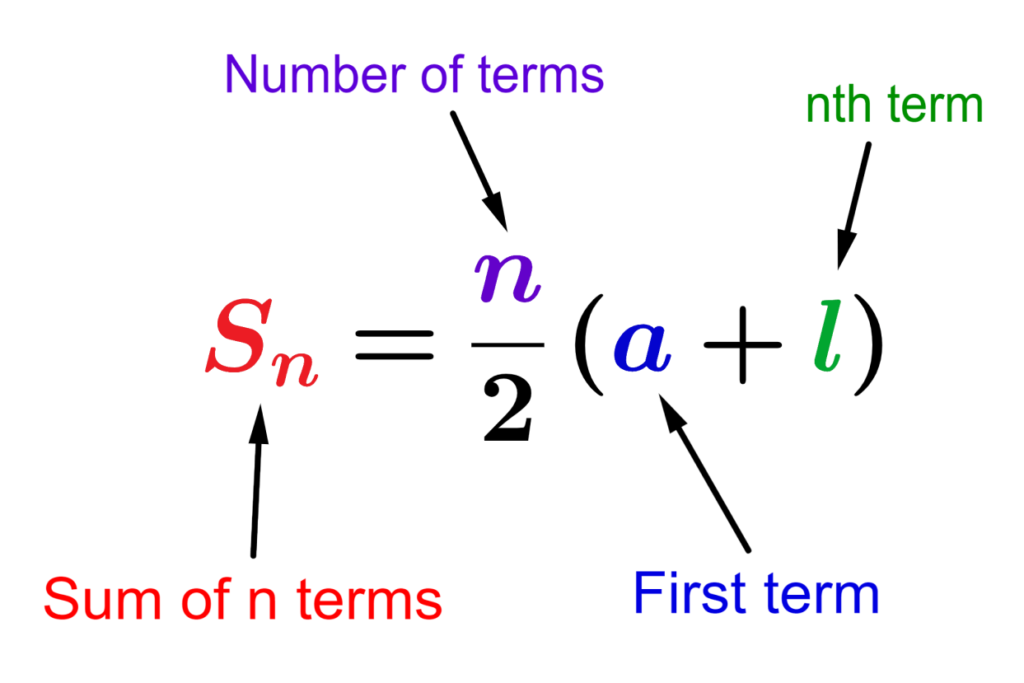
Sum Of Arithmetic Sequence Examples And Practice Problems Neurochispas
https://en.neurochispas.com/wp-content/uploads/2022/11/Formula-for-the-sum-of-an-arithmetic-sequence-1024x683.png
The sum of an arithmetic sequence is the sum of the first n terms of the sequence and it can found using one of the following formulas begin align S n frac n 2 2a n 1 d 0 3cm How explicit formulas work Here is an explicit formula of the sequence 3 5 7 a n 3 2 n 1 In the formula n is any term number and a n is the n th term This formula allows us to simply plug in the number of the term we are interested in and we will get the value of that term
We have different formulas associated with an arithmetic sequence used to calculate the n th term the sum of n terms of an AP or the common difference of a given arithmetic sequence The arithmetic sequence formula is given as N th Term a n a n 1 d S n n 2 2a n 1 d d a n a n 1 Nth Term of Arithmetic Sequence Just Keith 9 years ago Consider the sequence of numbers we will represent as A B C D E If B A C B D C E D then it is arithmetic If A B B C C D E D then it is geometric An arithmetic series is the sum of an arithmetic sequence A geometric series is the sum of a geometric sequence
More picture related to what is the formula for sum of arithmetic sequence

Sum Of Arithmetic Sequence 6 To 10 YouTube
https://i.ytimg.com/vi/J85ZUXvnfZM/maxresdefault.jpg

Question Video Finding The General Term Of An Arithmetic Sequence
https://media.nagwa.com/360132853472/en/thumbnail_l.jpeg

Arithmetic Sequence Formula Definition Examples Applications
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/formulas-of-arithmetic-sequence-formulas-of-arithmetic-sequence-1633103106.png
Actually the explicit formula for an arithmetic sequence is a n a n 1 D and the recursive formula is a n a n 1 D instead of a n a D n 1 Instead you can quickly find the sum of any arithmetic sequence by multiplying the average of the first and last term by the number of terms in the sequence Part 1 Assessing Your Sequence Download Article 1 Make sure you have an arithmetic sequence
If you wish to find any term also known as the latex nth latex term in the arithmetic sequence the arithmetic sequence formula should help you to do so The critical step is to be able to identify or extract known values from the problem that will eventually be substituted into the formula itself n k 1c c c c c n c

Arithmetic Series Summation Notation Formula Decorating Ideas
https://image1.slideserve.com/2645449/example-2-use-the-summation-formula-for-arithmetic-series-to-find-the-sum-l.jpg
Sum Of Arithmetic Sequence SEMI DETAILED LESSON PLAN IN MATHEMATICS
https://d20ohkaloyme4g.cloudfront.net/img/document_thumbnails/2c5c2f024c168d83238e4c0d12886c25/thumb_1200_1698.png
what is the formula for sum of arithmetic sequence - The sum of the members of a finite arithmetic progression is called an arithmetic series For example consider the sum This sum can be found quickly by taking the number n of terms being added here 5 multiplying by the sum of the first and last number in the progression here 2 14 16 and dividing by 2