what is non linear diophantine equation In mathematics a Diophantine equation is an equation typically a polynomial equation in two or more unknowns with integer coefficients for which only integer solutions are of interest A linear Diophantine equation equates to a constant the sum of two or more monomials each of degree one
Naive guesses about diophantine equations The most famous diophantine equation is the Fermat equation xd yd zd 0 For d 2 there are many integer solutions and for d 3 there are no positive integer solutions The proof To a contradiction modulo 5 Hence the original equation has no integer solutions Alternative Solution We could have looked at the equation modulo 3 to get 7y2 0 1mod3 or 2 y2 0 1mod3 multiply both sides by 2 to get 4y2 0 2mod3 i e y2 0 2mod3 We see if this is possible or not by testing each possible value for y ymod3
what is non linear diophantine equation
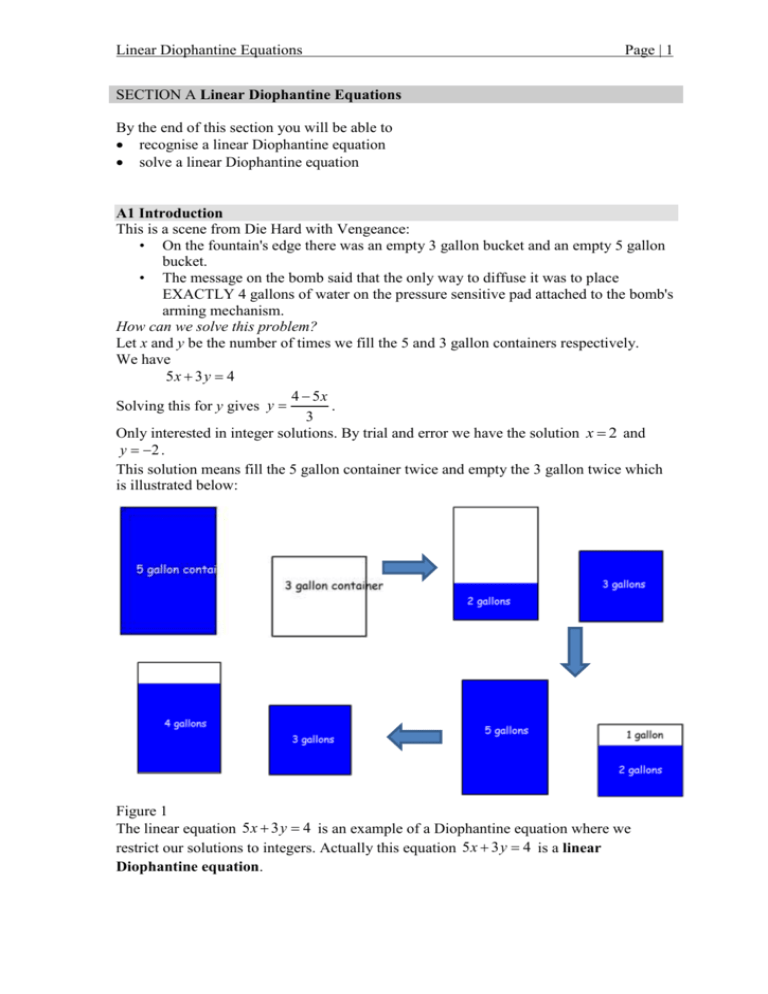
what is non linear diophantine equation
https://s3.studylib.net/store/data/006755500_1-262d0f3dd7be897d1f12efe36cf40b6c-768x994.png
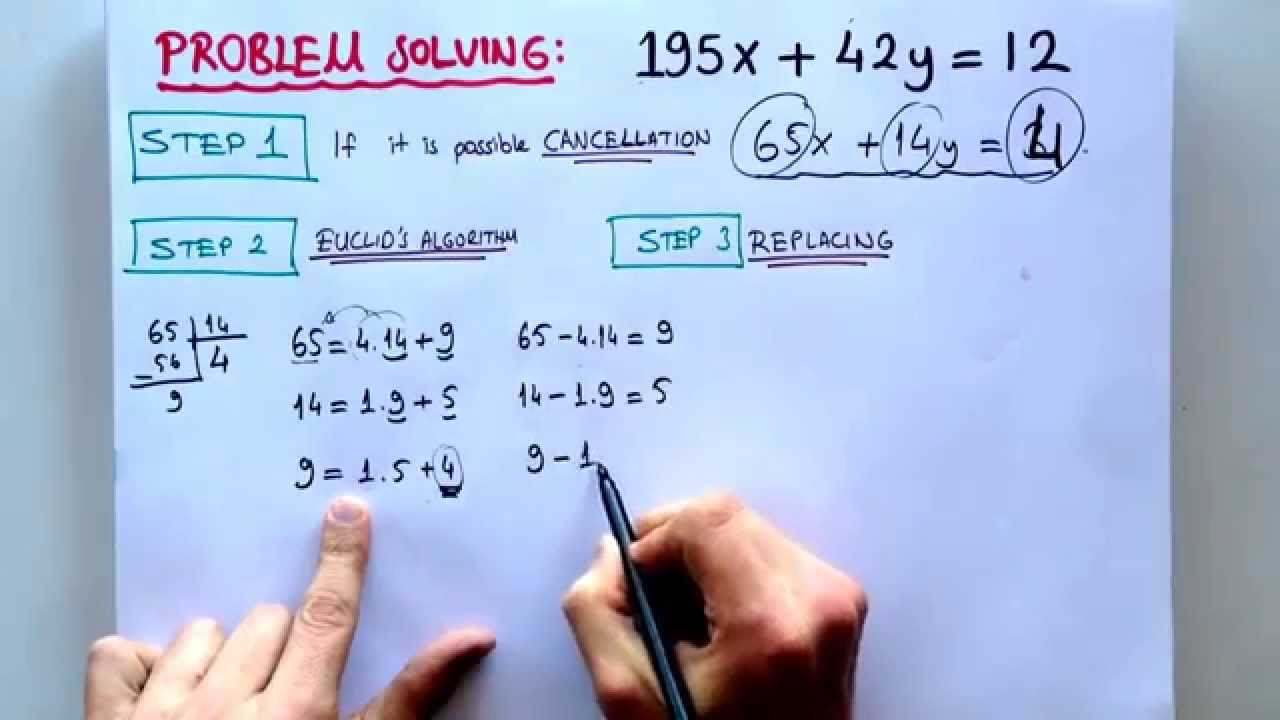
5mins LINEAR DIOPHANTINE EQUATION BY USING EUCLID S ALGORTIHM Tonguc
https://i.ytimg.com/vi/srE7JieiFM0/maxresdefault.jpg

Using The Euclidean Algorithm To Find Solutions To Linear Diophantine
https://i.ytimg.com/vi/JYaJDb6XN18/maxresdefault.jpg
Nonlinear Diophantine Equations In general solving a nonlinear Diophantine equation can be very difficult In this section we ll look at some examples of solving such an equation and showing that such an equation can t be solved Example Find all pairs of nonnegative integers such that Case 1 and Adding the two equations gives Thus A linear Diophantine equation in two variables is an equation of the general form 1 where solutions are sought with and integers Such equations can be solved completely and the first known solution was constructed by Brahmagupta Consider the equation 2 Now use a variation of the Euclidean algorithm letting and
5 1 Linear Diophantine Equations Diophantine equation is a polynomial equation with 2 or more integer unknowns 5 2 Linear Congruences Revisted 5 3 Non Linear Diophantine Equations 5 E Exercises 12 Solve in the nonnegative integers the equation 2x 1 xy 2 Linear Diophantine Equations Theorem 1 Let a b c be integers The equation ax by c has integer solutions if and only if gcd a b divides The Euclidean algorithm gives us a way of solving equations of the form ax by c when it is possible 3
More picture related to what is non linear diophantine equation

Linear diophantine equations 2 4 Linear Diophantine Equations
https://d20ohkaloyme4g.cloudfront.net/img/document_thumbnails/afbce601f9fe5acec25c4455a3d3be1b/thumb_1200_1553.png

N3 Simplify And Solve Linear Diophantine Equation Diophantine
https://i.pinimg.com/originals/3c/29/c7/3c29c76259b69e72a2309d95ad0a4113.jpg

Linear Diophantine Equations Ax By C YouTube
https://i.ytimg.com/vi/SCf-HrtYUMg/maxresdefault.jpg
A diophantine equation is an algebraic equation or system of equations in several unknowns and with integer or rational coefficients which one seeks to solve in integers or rational numbers The study of such equations goes back to antiquity Diophantine equation equation involving only sums products and powers in which all the constants are integers and the only solutions of interest are integers For example 3 x 7 y 1 or x2 y2 z3 where x y and z are integers Named in honour of the 3rd century Greek mathematician Diophantus of Alexandria these equations were
Further since it is easily checked that m 1 2 it follows that m 1 must have at least one prime divisor so by 6 4 n is even We now multiply together all congruences of the type 6 5 that is one for each prime dividing m 1 Since m 1 is squarefree the resulting modulus is m 1 Apply to a general linear Diophantine equation namely that if x y is an integer solution to ax by c then so will be x bk y ak where k is any integer If we substitute x bk for x and y ak for y we obtain a x bk b y ak c ax abk by abk c ax by c so if x y is a solution then so also is x bk y ak 3 Reducing

Linear Diophantine Equations Brilliant Math Science Wiki
https://ds055uzetaobb.cloudfront.net/image_optimizer/661be05e55f28eb482a1d2df198b9ef65bc23ba1.jpg

Solved Consider The Following Linear Diophantine Equations Chegg
https://media.cheggcdn.com/media/e8a/e8a640c4-f048-4c22-9130-027474f17618/phpVjWj7v.png
what is non linear diophantine equation - Nonlinear Diophantine Equations In general solving a nonlinear Diophantine equation can be very difficult In this section we ll look at some examples of solving such an equation and showing that such an equation can t be solved Example Find all pairs of nonnegative integers such that Case 1 and Adding the two equations gives Thus