what is cosec The cosecant csc The cosecant is the reciprocal of the sine It is the ratio of the hypotenuse to the side opposite a given angle in a right triangle A C B a c sin A opposite hypotenuse a c csc A hypotenuse opposite c a The secant sec The secant is the reciprocal of the cosine
Csc Csc Trigonometric Identities of Complementary Angles In geometry two angles are complementary if their sum is equal to 90 degrees Similarly when we can learn here the trigonometric identities for complementary angles Sin 90 Cos Cos 90 Sin Tan 90 Cot Cot 90 Tan Summary Secant sec is the reciprocal of cosine cos Cosecant cosec is the reciprocal of sin Cotangent cot is the reciprocal of tan Recall in case of a right angle triangle if we are given one length and one angle and we have to find a missing length or if we need to find a missing angle when two lengths are given we use SOH CAH TOA
what is cosec

what is cosec
https://www.petervis.com/mathematics/integration-solutions/integrate-cosec_2_x/step-02.gif
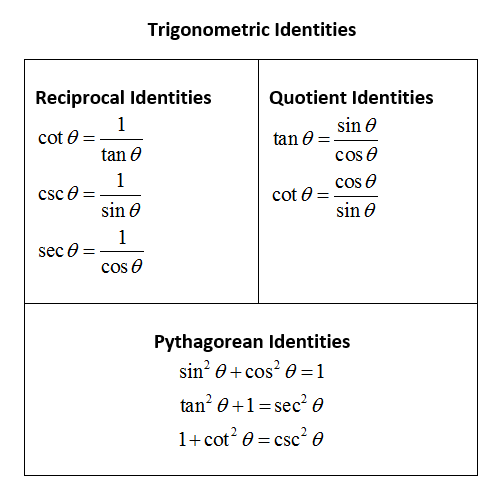
Sin X Cosec X 8 Socratic
https://useruploads.socratic.org/NVzgltr8R4uOxnLuNQUM_trigonometric identities.png

Ex 2 1 10 Find Principal Value Of Cosec 1 Root 2 Ex 2 1
https://d1avenlh0i1xmr.cloudfront.net/medium/18233501-de72-4db1-b339-b7ad391f1c43/slide10.jpg
Cosecant is one of the main six trigonometric functions and is abbreviated as csc x or cosec x where x is the angle In a right angled triangle cosecant is equal to the ratio of the hypotenuse and perpendicular Since it is the reciprocal of sine we write it as csc x 1 It will help you to memorize formulas of six trigonometric ratios which are sin cos tan sec cosec and cot Now look at all the capital letters of the sentence which are O H A H O and A Now suppose that O stands for opposite side H
So we can say tan sin cos That is our first Trigonometric Identity Cosecant Secant and Cotangent We can also divide the other way around such as Adjacent Opposite instead of Opposite Adjacent to get Cosecant Function csc Hypotenuse Opposite Secant Function sec Hypotenuse Adjacent Cosecant is one of the six trigonometric ratios which is also denoted as cosec or csc The cosecant formula is given by the length of the hypotenuse divided by the length of the opposite side in a right triangle There is an interesting relationship between the trigonometric ratios cosecant and sine which will be seen below
More picture related to what is cosec

Ex 2 1 10 Find Principal Value Of Cosec 1 Root 2 Finding Prin
https://d1avenlh0i1xmr.cloudfront.net/b8d036be-9ae5-492c-b0d1-2cea562fa31a/slide16.jpg

17 Reciprocal Functions Sec Cosec And Cot YouTube
https://i.ytimg.com/vi/lJiwIR4IG0s/maxresdefault.jpg

Question 4 Cosec X 2 Find Principal And General Solution
https://d77da31580fbc8944c00-52b01ccbcfe56047120eec75d9cb2cbd.ssl.cf6.rackcdn.com/8cc0a63f-b90e-4b28-a627-0bd8763e8f11/slide9.jpg
Course Trigonometry Trigonometric ratios review Google Classroom Review all six trigonometric ratios sine cosine tangent cotangent secant cosecant What are the trigonometric ratios C B A opposite adjacent hypotenuse Want to learn more about sine cosine and tangent Check out this video Trigonometry Course Trigonometry Finding reciprocal trig ratios Google Classroom About Transcript Sal finds all six trigonometric ratios sine cosine tangent secant cosecant and cotangent of an angle in a given right triangle Created by Sal Khan Questions Tips Thanks Want to join the conversation Sort by Top Voted
[desc-10] [desc-11]

A9 Evaluating Sec Csc Cot DocHub
https://dochub.com/reannahightower/dPB1mkMKO2qZ9aREOjyzDa/a9-evaluating-sec-csc-cot.jpg

Summary Of Trigonometric Identities
http://www.clarku.edu/~djoyce/trig/defining.jpg
what is cosec - So we can say tan sin cos That is our first Trigonometric Identity Cosecant Secant and Cotangent We can also divide the other way around such as Adjacent Opposite instead of Opposite Adjacent to get Cosecant Function csc Hypotenuse Opposite Secant Function sec Hypotenuse Adjacent