ways to factoring polynomials There are six different methods to factorising polynomials The six methods are as follows Greatest Common Factor GCF Grouping Method Sum or difference in two cubes Difference in two squares method General trinomials Trinomial method In this article let us discuss the two basic methods which we are using frequently to factorise the
There are some nice special forms of some polynomials that can make factoring easier for us on occasion Here are the special forms a2 2ab b2 a b 2 a2 2ab b2 a b 2 a2 b2 a b a b a3 b3 a b a2 ab b2 a3 b3 a b a2 ab b2 Let s work some examples with these Factoring Polynomials means decomposing the given polynomial into a product of two or more polynomials using prime factorization Learn how to determine the factors of the polynomials with definition methods examples
ways to factoring polynomials

ways to factoring polynomials
https://i.ytimg.com/vi/9MUDAr1PnlE/maxresdefault.jpg

How To Factor Polynomials The Easy Way YouTube
https://i.ytimg.com/vi/U6FndtdgpcA/maxresdefault.jpg
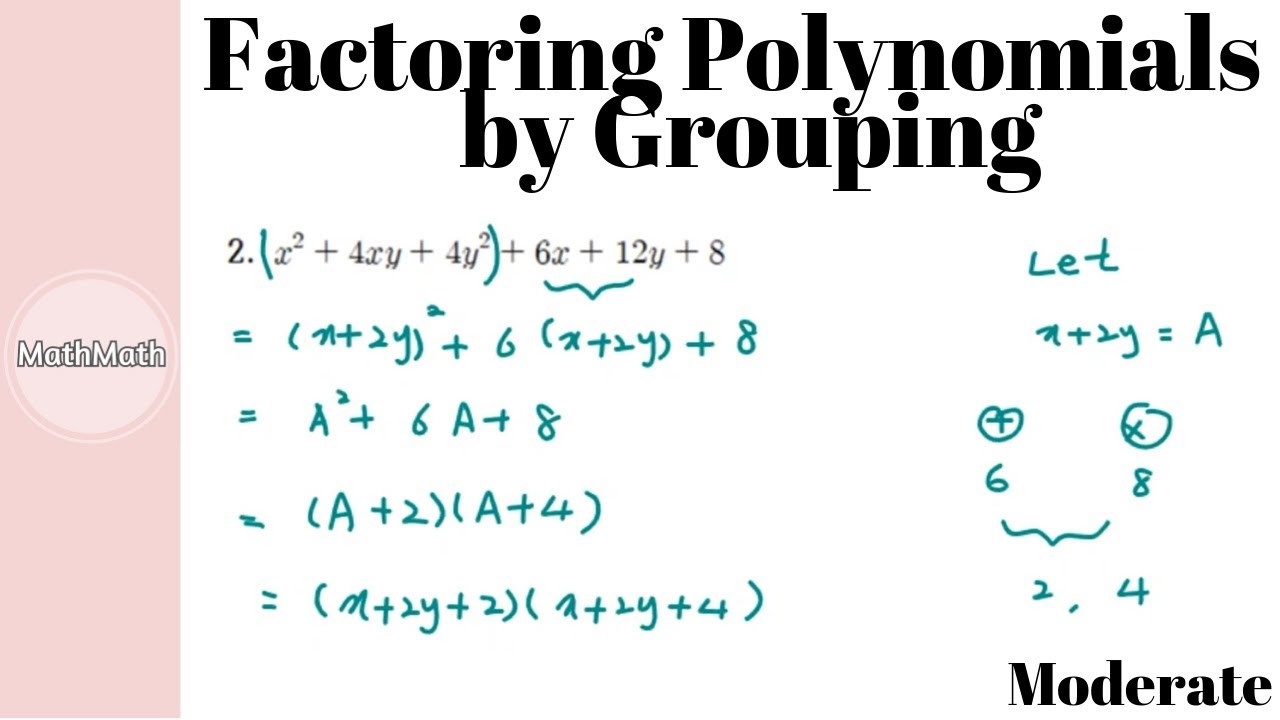
Polynomials HOW TO Factoring Polynomials By Grouping Moderate Level
https://i.ytimg.com/vi/Q0hAA_KEFhU/maxresdefault.jpg
About this unit Let s get equipped with a variety of key strategies for breaking down higher degree polynomials From taking out common factors to using special products we ll build a strong foundation to help us investigate polynomial functions and prove identities To factor the GCF out of a polynomial we do the following Find the GCF of all the terms in the polynomial Express each term as a product of the GCF and another factor
To factor out the GCF of a polynomial we first determine the GCF of all of its terms Then we can divide each term of the polynomial by this factor as a means to determine the remaining factor after applying the distributive property in reverse The following factoring methods will be used in this lesson Factoring out the GCF The sum product pattern The grouping method The perfect square trinomial pattern The difference of squares pattern What you will learn in this lesson
More picture related to ways to factoring polynomials

How To Factor Polynomials Step by Step Mashup Math
http://static1.squarespace.com/static/54905286e4b050812345644c/t/641dea92e6614b2dbc0eafb3/1679682194747/Banner-Image.jpg?format=1500w

How To Factor Third Degree Polynomials Polynomial Functions For
https://media.nagwa.com/852167949057/en/thumbnail_l.jpeg

Factor Polynomials Understand In 10 Min YouTube
https://i.ytimg.com/vi/KUMhpKGwpCY/maxresdefault.jpg
To factor a polynomial Start by identifying any common factors and you can either use the following factoring methods Use the difference of squares or sum difference of cubes formulas for binomials Group the terms for polynomials with four or more terms Use the quadratic formula for quadratic polynomials We will look at 3 common ways in which a polynomial can be factored grouping substitution and using identities Contents Factoring Polynomials by Grouping Factoring by Substitution Factoring Polynomials using Identities Factoring Polynomials by Grouping We often see the grouping method applied to polynomials with 4 terms
General Strategy for Factoring Polynomials See Figure PageIndex 1 How to Factor Polynomials Is there a greatest common factor Factor it out Is the polynomial a binomial trinomial or are there more than three terms If it is a binomial Is it a sum Of squares Sums of squares do not factor Of cubes Use the sum of cubes pattern Factor the greatest common factor of a polynomial Factor a trinomial Factor by grouping Factor a perfect square trinomial Factor a difference of squares Factor the sum and difference of cubes Factor expressions using fractional or
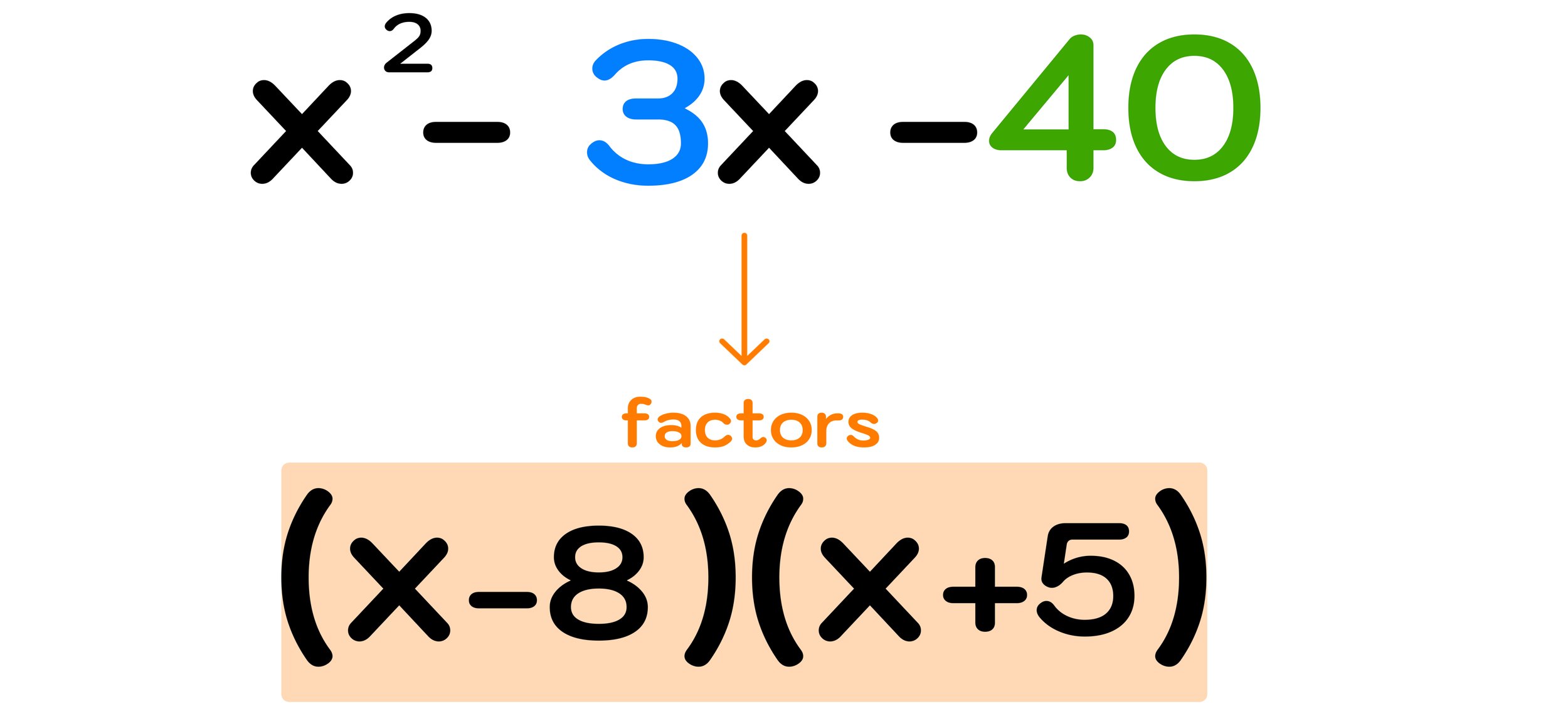
How To Factor Polynomials Step by Step Mashup Math
https://images.squarespace-cdn.com/content/v1/54905286e4b050812345644c/033fc137-440e-4b1f-acac-7bc061ff641d/Fig09.jpg
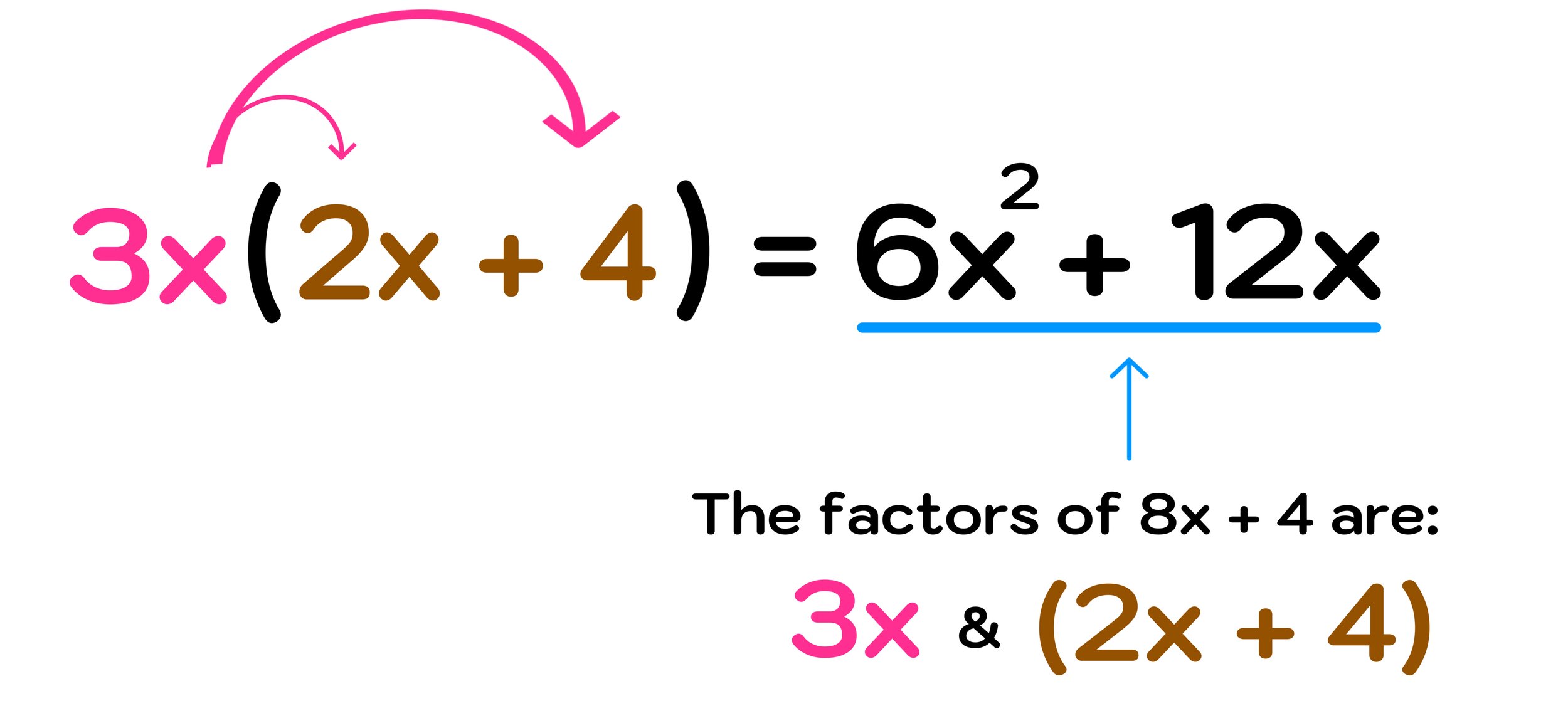
How To Factor Polynomials Step by Step Mashup Math
https://images.squarespace-cdn.com/content/v1/54905286e4b050812345644c/82cd70f3-2085-45a1-9cc3-aa0aa778c5fb/Figure-04.jpg
ways to factoring polynomials - About this unit Let s get equipped with a variety of key strategies for breaking down higher degree polynomials From taking out common factors to using special products we ll build a strong foundation to help us investigate polynomial functions and prove identities