two important limits Two important Limits What we need To figure out the derivatives of trig functions we need Two extremely important limits derived below limx 0 sin x x 1 and limx 0 1 cos x x 0 lim x 0 sin x x 1 and lim x 0 1 cos x x 0 The
The first two limit laws were stated in Two Important Limits and we repeat them here These basic results together with the other limit laws allow us Recognize the basic limit laws Use the limit laws to evaluate the limit of a function Evaluate the limit of a function by factoring Use the limit laws to evaluate the limit of a polynomial or rational function Evaluate the limit of a function by factoring or by using conjugates
two important limits
two important limits
https://embed-ssl.wistia.com/deliveries/b661675f6faf47c22bd4655b8f30e2ee.bin
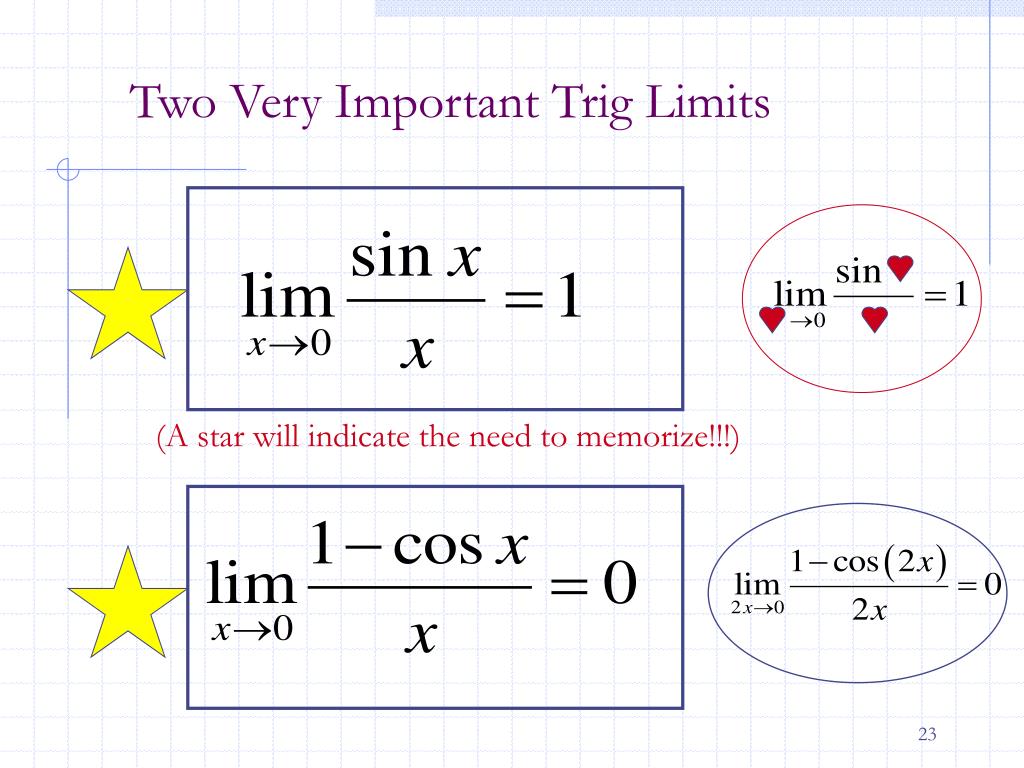
PPT Evaluating Limits Analytically PowerPoint Presentation Free
https://image3.slideserve.com/6602287/two-very-important-trig-limits-l.jpg

Some important limits TUTOR TTD
https://tutorttd.com/wp-content/uploads/2021/10/some-important-limits.jpg
Two Important Limits Let a be a real number and c be a constant displaystyle lim x to a x a displaystyle lim x to a c c We can make the following observations about these two limits For the first limit observe that as x approaches a so does f x because f x x Consequently displaystyle lim x to a x a We begin this chapter by examining why limits are so important Then we go on to describe how to find the limit of a function at a given point Not all functions have limits at all points and we discuss what this means and how we can tell if a function does or does not have a limit at a particular value
We will discuss the interpretation meaning of a limit how to evaluate limits the definition and evaluation of one sided limits evaluation of infinite limits evaluation of limits at infinity continuity and the Intermediate Value Theorem Definition Let be a function defined at all values in an open interval containing with the possible exception of itself and let be a real number If all values of the function approach the real number as the values of approach the number then we say that the limit of as approaches is
More picture related to two important limits

Ppt 1 06 Limits Involving Infinity Powerpoint Presentation Free 2AF
https://image1.slideserve.com/1968782/slide11-l.jpg

PPT Advanced Mathematics PowerPoint Presentation Free Download ID
https://image3.slideserve.com/5601988/slide4-l.jpg

Ppt 1 06 Limits Involving Infinity Powerpoint Presentation Free 2AF
https://image1.slideserve.com/1968782/slide9-l.jpg
Definition We say that the limit of f x f x is L L as x x approaches a a and write this as lim x af x L lim x a f x L provided we can make f x f x as close to L L as we want for all x x sufficiently close to a a from both sides without actually letting x x be a a This is not the exact precise definition of a limit We begin by restating two useful limit results from the previous section These two results together with the limit laws serve as a foundation for calculating many limits Evaluating Limits with the Limit Laws The first two limit laws were stated in link and we repeat them here
[desc-10] [desc-11]

Important Limits Of Exercise YouTube
https://i.ytimg.com/vi/yVoVaJn_44Q/maxresdefault.jpg
The Power Of Limits Say No To Overtime And Yes To Career Growth
https://miro.medium.com/v2/resize:fit:1200/0*kGT8gI7tE-u0vdSW
two important limits - [desc-13]