third law of logarithms proof I was asked to prove the third law of logarithm where log A y y log A My proof is that log A y y log A If log A y log 10 log A y That means that log 10 log A y y log A log 10 cancels out leaving log A y y log A
Proof Step 1 Let m log a x and n log a y Step 2 Write in exponent form x a m and y a n Step 3 Multiply x and y x y a m a n a m n Step 4 Take log a of both sides and evaluate log a xy log a a m n log a xy m n log a a log a xy m n In this lesson we will prove three logarithm properties the product rule the quotient rule and the power rule Before we begin let s recall a useful fact that will help us along the way log b b c c
third law of logarithms proof

third law of logarithms proof
https://i.ytimg.com/vi/lrDl6EUlk4M/maxresdefault.jpg

Logarithm Rules aka Log Laws Explained With Examples Maths For Kids
https://i0.wp.com/maths.forkids.education/wp-content/uploads/2020/05/Log-Laws-rules-of-logarithm.jpg?fit=1000%2C798&ssl=1

The Third Law Of Logarithms Useful For VIII Class IX Class X CLASS
https://i.ytimg.com/vi/3IclZVNSY3A/maxresdefault.jpg
Sal proves the logarithm quotient rule log a log b log a b and the power rule k log a log a Created by Sal Khan Questions Tips Thanks Want to join the conversation Log in Sort by Top Voted Ajib Minallah 11 years ago what grade is logs for 9 votes Upvote Downvote Flag Christi 11 years ago Using the third logarithm law we have log x 5 5 log x We have expressed it as a multiple of a logarithm and it no longer involves an exponent Note 1 Each of the following is equal to 1 log 6 6 log 10 10 log x x log a a 1 The equivalent statements using ordinary exponents are as follows 6 1 6
Intro to logarithm properties Learn about the properties of logarithms and how to use them to rewrite logarithmic expressions For example expand log 3a These properties apply for any values of M N and b for which each logarithm is defined which is The Quotient Rule for Logarithms Proof How to Given the logarithm of a quotient use the quotient rule of logarithms to write an equivalent difference of logarithms Example PageIndex 2 Using the Quotient Rule for Logarithms Exercise PageIndex 2 Using the Power Rule for Logarithms The Power Rule for Logarithms
More picture related to third law of logarithms proof
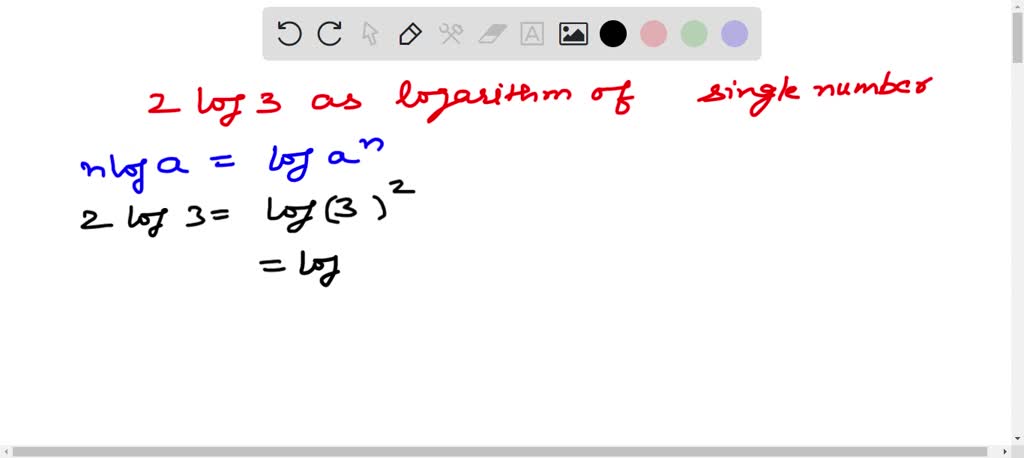
SOLVED Write 2 Log3 As The Logarithm Of A Single Number 2 Log3 log3 2
https://cdn.numerade.com/previews/d43986b1-bda4-4481-90a4-c6ccd20c88a0_large.jpg

6 4 Power Law Of LOGARITHMS full Lesson Grade 12 MHF4U Jensenmath
https://i.ytimg.com/vi/eVm1RM5A-AA/maxresdefault.jpg

Proof Of Quotient Rule Of Logarithms
https://farm5.staticflickr.com/4215/34937634253_4080acc4d1_o.jpg
Student Solutions This resource is from Underground Mathematics Warm up Take a look at these results log3 2 log3 5 log3 10 log2 15 log2 3 log2 5 2log5 7 log5 49 1 3 log5 64 log5 4 log5 7 log7 11 log5 11 How can you change the input values so that the equations still hold The 3 main logarithm laws are The Product Law log mn log m log n The Quotient Law log m n log m log n The Power Law log m k k log m The three fundamental laws of logarithms are shown below Rules when using the Laws of Logarithms The rules for the laws of logarithms are
Theorem Let x y b R 0 x y b R 0 be strictly positive real numbers Let a R a R be any real number such that a 0 a 0 and a 1 a 1 Let loga log a denote the logarithm to base a a Then Change of Base of Logarithm logb x loga x loga b log b x log a x log a b Sum of Logarithms Solution Adapting the ideas Take a look at these results log3 2 log3 5 log3 10 log 3 2 log 3 5 log 3 10 log2 15 log2 3 log2 5 log 2 15 log 2 3 log 2 5 2log5 7 log5 49 2 log 5 7 log 5 49 13log5 64 log5 4 1 3 log 5 64 log 5 4 log5 7 log7 11 log5 11 log 5 7 log 7 11 log 5

0 Result Images Of What Is Difference Between Natural Log And Log PNG
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/natural-log-formulas-1618943893.png

Logarithm Theory Of Logarithms Laws Etc ClassNotes ng
https://i0.wp.com/classnotes.ng/wp-content/uploads/2020/04/1-4.png?resize=415%2C632&ssl=1
third law of logarithms proof - We can use the power rule to expand logarithmic expressions involving negative and fractional exponents Here is an alternate proof of the quotient rule for logarithms using the fact that a reciprocal is a negative power logb A C logb AC 1 logb A logb C 1 logbA 1 logbC logbA logbC