sum of arithmetic progression series The sum of the members of a finite arithmetic progression is called an arithmetic series For example consider the sum This sum can be found quickly by taking the number n of terms being added here 5 multiplying by the sum of the first and last number in the progression here 2 14 16 and dividing by 2 In the case above this gives the equation
Advanced Topic Summing an Arithmetic Series To sum up the terms of this arithmetic sequence a a d a 2d a 3d use this formula Learn the general form of the arithmetic series formula and the difference between an arithmetic sequence and an arithmetic series Discover the partial sum notation and how to use it to calculate the sum of n terms
sum of arithmetic progression series

sum of arithmetic progression series
https://i2.wp.com/www.aplustopper.com/wp-content/uploads/2016/08/Arithematic-progression-formula.jpg?resize=1299%2C1308&ssl=1

Sum Of Arithmetic Sequence 6 To 10 YouTube
https://i.ytimg.com/vi/J85ZUXvnfZM/maxresdefault.jpg
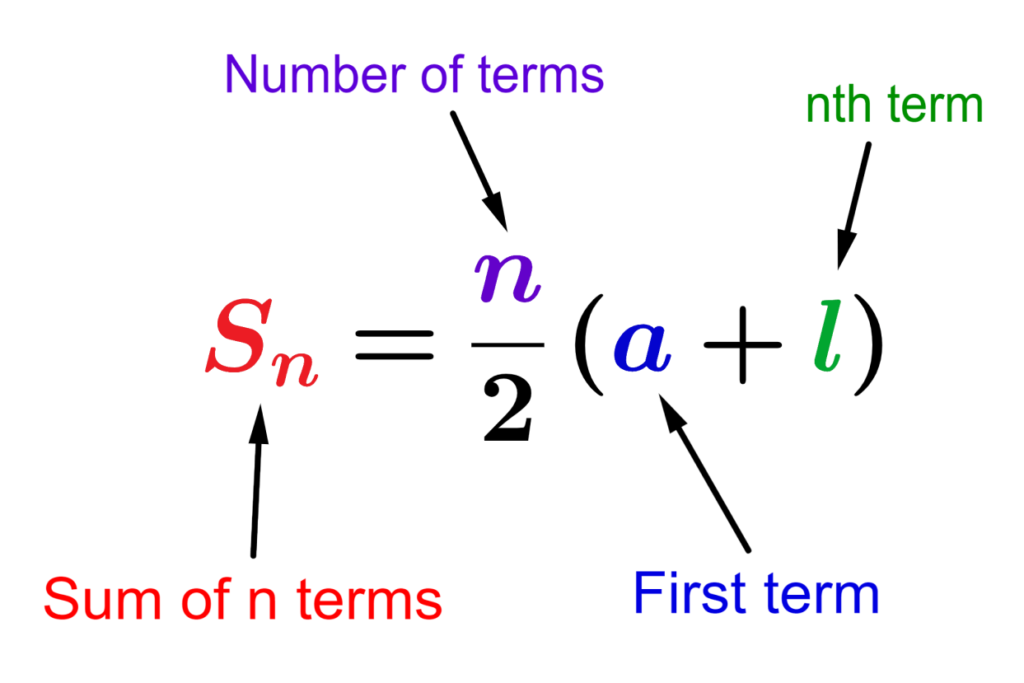
Sum Of Arithmetic Sequence Examples And Practice Problems Neurochispas
https://en.neurochispas.com/wp-content/uploads/2022/11/Formula-for-the-sum-of-an-arithmetic-sequence-1024x683.png
How to calculate the sum of the first n numbers in an arithmetic progression The sum of the first n term of an arithmetic progression is given by Formula First n Numbers in an AP S n n 2 An arithmetic series is the sum of the terms of an arithmetic sequence The n th partial sum of an arithmetic sequence can be calculated using the first and last terms as
We can find the sum of an arithmetic sequence using the following Sum of Arithmetic Sequence Calculator by entering the first term a common difference d and the number of terms Uses mathematical induction to prove the formula for the sum of a finite arithmetic series Provides an animation which illustrates the gist of the formula
More picture related to sum of arithmetic progression series

Arithmetic Sequence Videos Concepts Formulas And Solved Examples
https://d1whtlypfis84e.cloudfront.net/guides/wp-content/uploads/2018/01/24064251/Arithmetic-Progression_V_04-613x1024.jpg

Arithmetic Sequences And Arithmetic Series Membership YouTube
https://i.ytimg.com/vi/mxEIFO8vXKY/maxresdefault.jpg

Maths GEOMETRIC PROGRESSION
https://1.bp.blogspot.com/-SBjFM4vZPRM/V4H1VfsxyfI/AAAAAAAAACk/utDOb2IYeHowLApTCOvQqDfqWSU8VCW9QCLcB/s1600/Nterm.jpg
For an arithmetic progression with initial term a 1 and common difference d the sum of the first n terms is S n frac n 2 big 2a 1 n 1 d big What is the sum of the first 50 odd positive integers When the values of the first term and the last term are known In this case the sum of arithmetic sequence or sum of an arithmetic progression is begin align s n frac n 2 a a n end align
An arithmetic series is the sum of all the terms of an arithmetic sequence All infinite arithmetic series diverge As for finite series there are two primary formulas used to compute their value In this article we explain the arithmetic sequence definition clarify the sequence equation that the calculator uses and hand you the formula for finding arithmetic series sum
Cambridge AS Level Mathematics 9709 Pure Mathematics 1 Past Paper
https://1.bp.blogspot.com/-TC-_MusASuY/X3MC4FgMd3I/AAAAAAAAAJY/nEDzaAC1bG8jOTGPGtQdDnrYL2yYi51TACLcBGAsYHQ/w1200-h630-p-k-no-nu/formula%2Bfor%2Barithmetic%2Band%2Bgeometric%2Bprogressions%2Band%2Bseries.PNG

Question Video Finding The Number Of Terms That Make The Sum Of A
https://media.nagwa.com/964167502805/en/thumbnail_l.jpeg
sum of arithmetic progression series - The sum of n terms of AP is the sum addition of first n terms of the arithmetic sequence It is equal to n divided by 2 times the sum of twice the first term a and the product of the