square root of 10368 by division method Square Root by Long Division Method The most commonly used method to find the square root of a number is the division method In this article we will learn how to solve square root
We can determine the square root of perfect squares by prime factorisation method But if the number is not a perfect square then it is difficult to find the square root of it Hence we then use long division method For example Factor 10368 72 2 times 2 Rewrite the square root of the product sqrt 72 2 times 2 as the product of square roots sqrt 72 2 sqrt 2 Take the square root of 72 2
square root of 10368 by division method
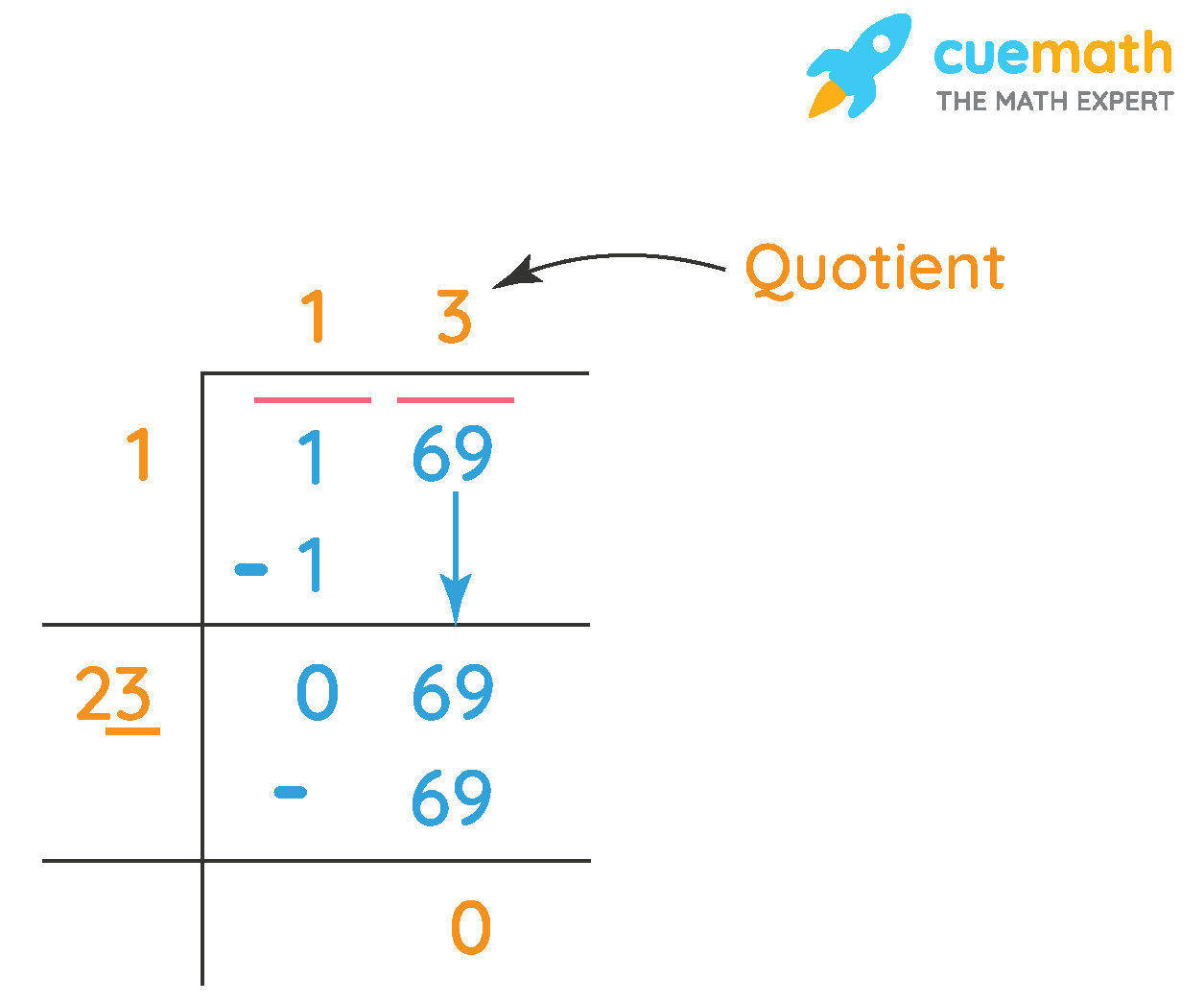
square root of 10368 by division method
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/finding-square-root-of-perfect-square-numbers-by-division-method-1620887862.png

Square Root Of 2 By Division Method Correct To Two Decimal Place
https://hi-static.z-dn.net/files/d58/2665ca36f83eb89663079754db2cb8e4.jpg

Find The Square Root Of The Following Numbers By Division Method
https://hi-static.z-dn.net/files/df3/13af49345a21c30902eee6e83966f56c.jpg
Steps of finding Square root by division method Step 1 Make pair of digits of given number starting with digit at one s place For ease of calculation put bar on each pair The square root by Long Division method is a manual technique that involves dividing a number into digit pairs and iteratively estimating the square root by refining guesses based on remainders This method provides
In this article we will study Finding Square Root by Division Method with How to Find Square Root by Long Division Steps to find Square Root by Division Method Rules and Solved Examples The long division sqrt square nthroot msquare square le ge frac msquare msquare cdot div x circ pi left square right frac d dx frac partial partial x int
More picture related to square root of 10368 by division method

10368find The Square Root Of 10368 By Long Division Method Brainly in
https://hi-static.z-dn.net/files/dcb/0ddcee6582839b14c907213a8457f39b.png

Find Square Root Of 9216 By Division Method Brainly in
https://hi-static.z-dn.net/files/d39/3333eb142c34f9625ae1a17a11e92d4f.jpg

How Can We Find Square Root By Division Method Brainly in
https://hi-static.z-dn.net/files/d93/ed69f535ae9ba3f8b380ae093a94344e.jpg
Given an integer X which is a perfect square the task is to find the square root of it by using the long division method Examples Input N 484 Output 22 22 2 484 Input N 144 Output 12 12 2 144 Approach The square root calculator finds the square root of the given radical expression If a given number is a perfect square you will get a final answer in exact form If a given number is not a
The long division method to find square root is a very popular and easy method to calculate the accurate roots of numbers In this method we observe five main steps such as divide In this section you will learn how to find square root of a number step by step Let us find the square root of 104976 step by step using long division method Step 1 Separate the digits

Find The Square Roots Of The Following Numbers By Division Method 3600
https://hi-static.z-dn.net/files/db6/0f4b652541b90660fbd61ce168126294.jpg

Square Root Of 8100 By Division Method Brainly in
https://hi-static.z-dn.net/files/dc2/674cecc7ffa2f246406685fd23a64bf1.jpg
square root of 10368 by division method - The square root by Long Division method is a manual technique that involves dividing a number into digit pairs and iteratively estimating the square root by refining guesses based on remainders This method provides