sin x formula in terms of e This formula can be interpreted as saying that the function e is a unit complex number i e it traces out the unit circle in the complex plane as ranges through the real numbers Here is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis measured counterclockwise and in radians
Using these and Euler s formula we can get that e ix e i x i sin x cos x i sin x cos x If you are not comfortable with it e iz e iz sin z is false The correct formula is frac e iz e iz 2i sin z Also your formulas ii and iii are missing the first order terms
sin x formula in terms of e
sin x formula in terms of e
https://media.cheggcdn.com/media/614/61475e60-1b0b-4aea-a60d-387a2b1a259b/phplY72g0

Taylor Series Formula
https://sigmatricks.com/wp-content/uploads/2021/02/Taylor-Series.jpg
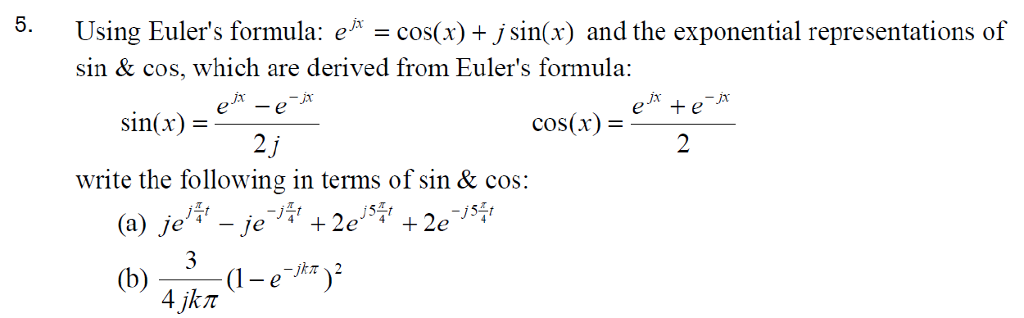
Solved 5 Using Euler s Formula E Cos x J Sin x And Chegg
https://media.cheggcdn.com/media/a42/a423f3dc-ead2-4cad-9e95-ff90af654595/phpKKlJa8.png
2 sin 1 cos 2 Multiple angle formulas for the cosine and sine can be found by taking real and imaginary parts of the following identity which is known as de Moivre s formula cos n Euler s formula allows for any complex number x x to be represented as e ix eix which sits on a unit circle with real and imaginary components cos x cosx and sin x sinx respectively Various operations such as finding the roots of
Solution We have Euler s formula e 2ix cos 2x i sin 2x nonumber so cos 2x text Re e 2ix The complex replacement trick is to replace cos 2x by e 2ix We get justification below I c int e x From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that were immensely painful to prove back in high school
More picture related to sin x formula in terms of e

Cos 2 Theta RydneerilPalmer
https://i.pinimg.com/736x/95/9a/6c/959a6cf17014e967576176894286b9c9.jpg

Trigonometric Identities 1 Conditional Trigonometrical Identities We
https://i.pinimg.com/originals/67/48/a4/6748a4a3857169c6750de56e27c306bf.jpg

Solved 5 Euler s Equations Are Defined As Sin x Cos x E Chegg
https://media.cheggcdn.com/media/4d2/4d2d9d09-a130-4ef5-a59d-0ddccc8c1ee9/php5vps32.png
Euler s formula is a relationship between exponents of imaginary numbers and the trigonometric functions For example if then Relationship to sin and cos In Euler s formula if we replace A key to understanding Euler s formula lies in rewriting the formula as follows e i x cos x i sin x where The right hand expression can be thought of as the unit complex number with angle x The left hand
Use Euler s formula to express in terms of sine and cosine Given that 1 what trigonometric identity can be derived by expanding the exponentials in terms of trigonometric functions One way to do that is to define exp mathbb C to mathbb C z mapsto sum n ge 0 frac z n n This implies that exp a exp b exp a b for all complex a

Solved Use The Reduction Formula Integral X alpha E beta X Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/a77/a77790a6-86ff-4de1-b7f3-a0baeba4e4e6/phpbDZjHS.png

What Is An Hyperbolic Function Math Trigonometric Functions 1230332
http://www.sosmath.com/trig/hyper/hyper01/img12.gif
sin x formula in terms of e - 2 sin 1 cos 2 Multiple angle formulas for the cosine and sine can be found by taking real and imaginary parts of the following identity which is known as de Moivre s formula cos n
