sin 1 x is not uniformly continuous

sin 1 x is not uniformly continuous Prove that the function defined by f x sin 1 x is not uniformly continuous on the interval 0 1 Hint Consider for example x 1 2n and y 1 2n 1 2 I have

Note In a frac pi 2 for some a 0 f x is continuous That is f x is continuous on a closed and bounded interval and so is uniform continuous on the interval The only Using this theorem we can give an easier proof that the function in Example 3 5 6 is not uniformly continuous Solution Consider the two sequences u n 1 n 1 and v n 1 n for all

sin 1 x is not uniformly continuous

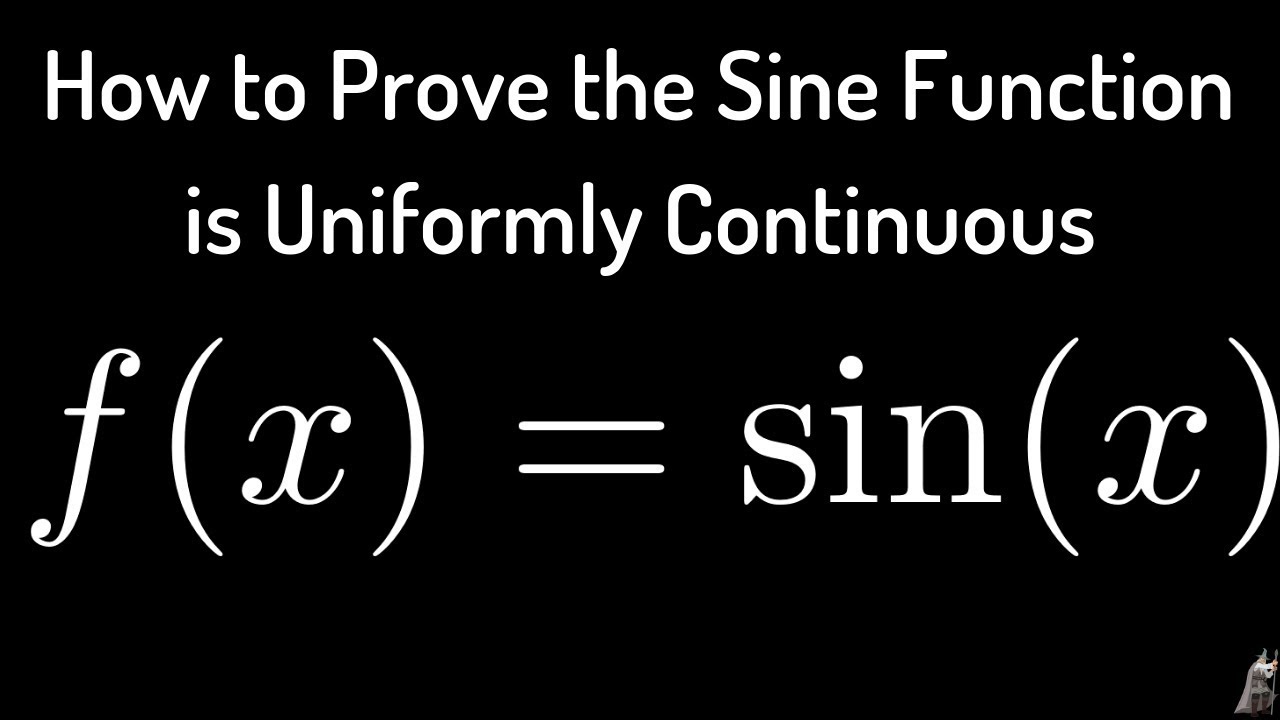
sin 1 x is not uniformly continuous
https://i.ytimg.com/vi/rltNzAfhSNg/maxresdefault.jpg

Example 26 Find Derivative Of F x Sin 1 X Class 12 Examples
https://d77da31580fbc8944c00-52b01ccbcfe56047120eec75d9cb2cbd.ssl.cf6.rackcdn.com/477f41a7-afb2-4287-8a1c-36820ef2a899/slide3.jpg

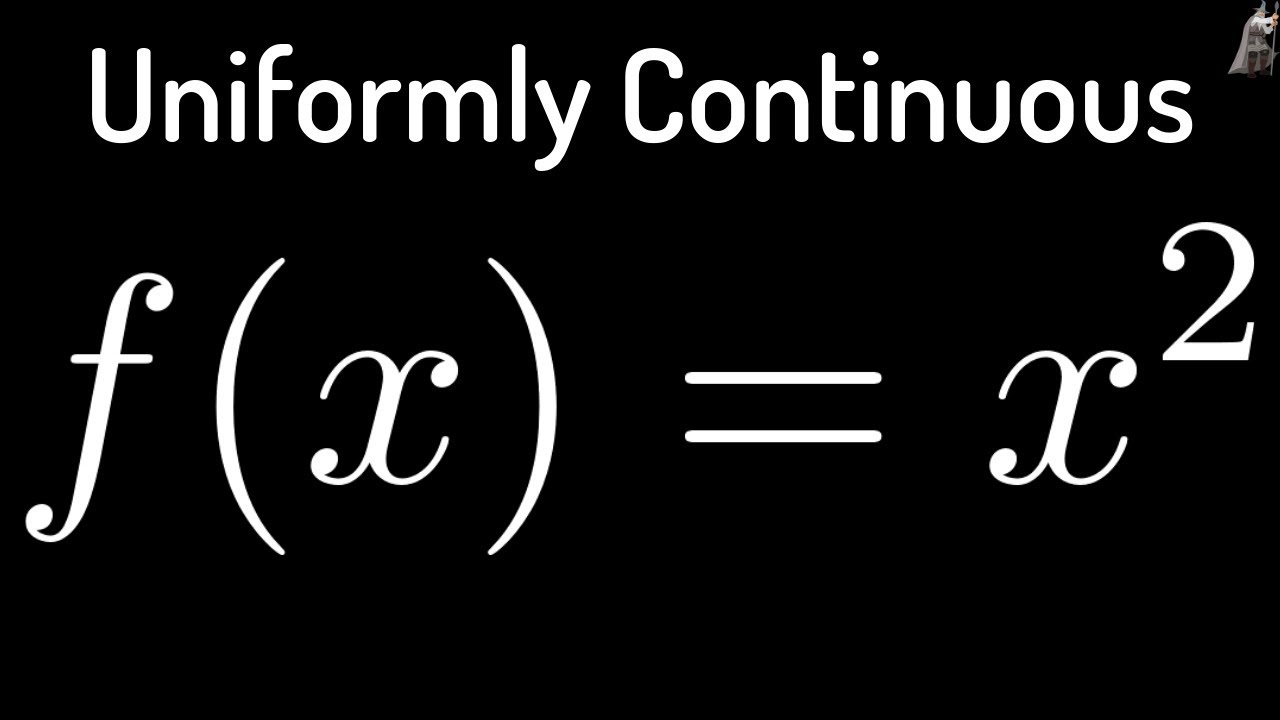
How To Prove A Function Is Continuous On An Open Interval
https://i.ytimg.com/vi/U-UmtZkCHwU/maxresdefault.jpg

Answer link The function as given is not continuous at 0 as 0sin 1 0 is not defined However we may make a slight modification to make the function continuous M11 Exercise sheet 3 Let f x sin 1 x for 0 x Prove that f is not uniformly continuous on 0 1 Let f x 1 1 jxj for real x Prove that f is uniformly continuous on R Let f x 1 x for

F x 1 x is not uniformly continuous on 0 1 because s n 1 n is Cauchy in 0 1 but f s n is not Cauchy Idea of Proof Since s n is Cauchy the inputs s n and s m are close to each F x x cdot sin frac 1 x in the interval 0 infinity is uniformly continuous using the following definition

More picture related to sin 1 x is not uniformly continuous

Solved How To Show That sin E x Is Not Uniformly 9to5Science
https://sgp1.digitaloceanspaces.com/ffh-space-01/9to5science/uploads/post/avatar/61537/template_how-to-show-that-sin-e-x-is-not-uniformly-continuous-on-mathbb-r20220819-1785152-1t1zzn7.jpg

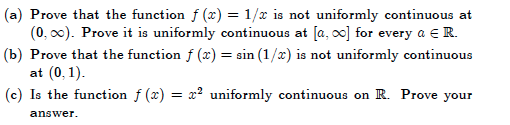
a Prove That The Function F x 1 x Is Not Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/6c3/6c32e954-3cf4-45e4-926f-7b639c97c15c/phpwAaN6e.png

Math Proving Or Disproving Uniform Continuity Of Various Real
https://i.stack.imgur.com/O2zF6.png

You can choose x depending on because x is quantified before Alternatively we have 1 n 1 n 1 0 but f 1 n f 1 n 1 n n 1 1 And by the The facts that 1 sin 1 x 1 for all x 0 and f 0 0 imply that x2 f x x2 for all x Since lim x 0 x2 0 and lim x 0 x2 0 it follows that lim x 0 f x 0 f 0 by

Proof Since fis continuous on the closed bounded interval 0 1 it is uniformly continuous on 0 1 by the Uniform Continuity Theorem It remains to show that fdoes not satisfy a Lipschitz No sin 1 x is not continuous on the interval 0 1 because it is not defined at x 0 The function has a vertical asymptote at x 0 which means it has a break in its graph and does

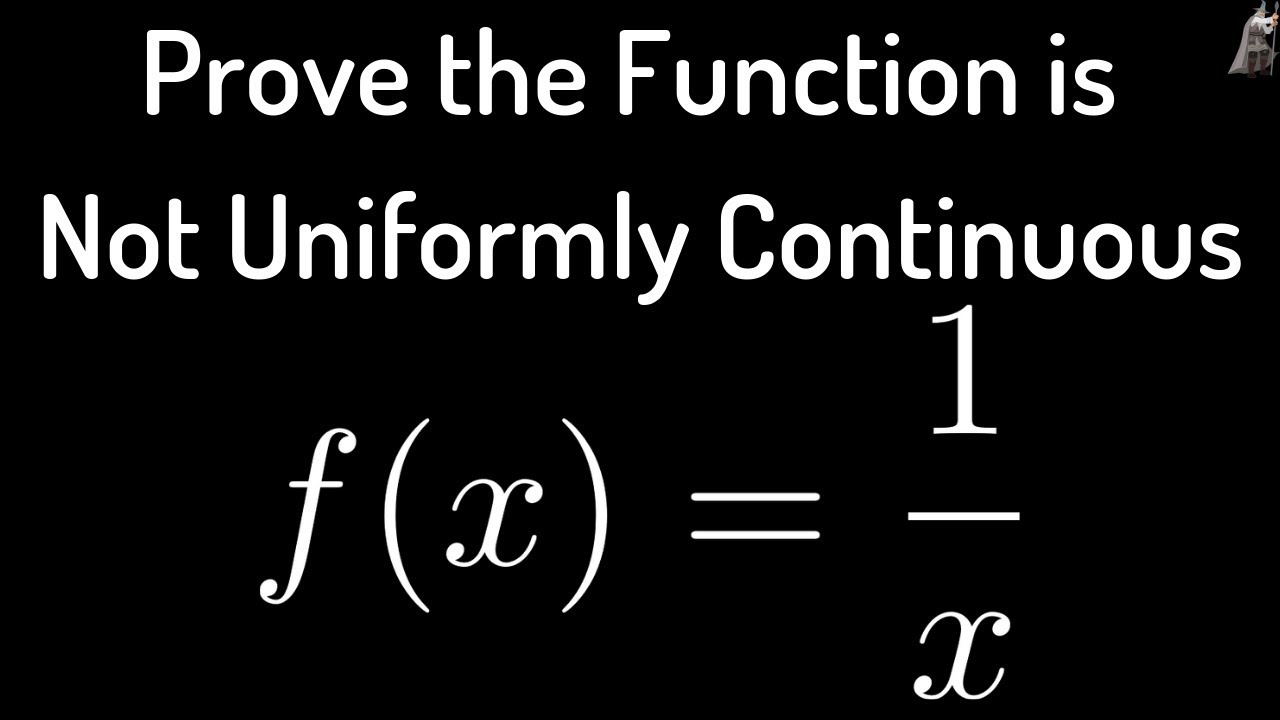
Function That Is Uniformly Continuous But Not Lipschitz Lipstutorial
https://i.ytimg.com/vi/PskrtRJx0Zk/maxresdefault.jpg

Example 3 Show i Sin 1 2x root 1 x2 2 Sin 1 X Examples
https://d1avenlh0i1xmr.cloudfront.net/1c940fc4-c336-4ddd-8292-036f97045a9a/slide3.jpg

sin 1 x is not uniformly continuous - The sine function is periodic so what you could do is read a proof that every continuous real valued function on a closed bounded interval a b is uniformly continuous and so sin on