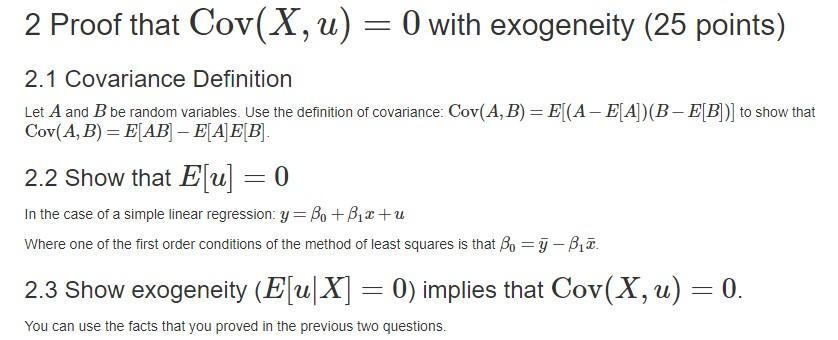show that cov x y e xy e x e y My textbook claims that cov X Y E X E X Y E Y It then claims that multiplying this out and using linearity we have an equivalent expression cov X Y E XY
Rewrite as Cov X Y E Y X 0 which is true because E Y X of Y is an orthogonal projection onto space of functions measurable with respect to sigma X Cov X Y E X X Y Y E XY XY Y X X Y E XY XE Y Y E X X Y E XY E X E Y I Covariance formula E XY E X E Y or expectation of product minus product of expectations
show that cov x y e xy e x e y

show that cov x y e xy e x e y
https://s2.studylib.net/store/data/012025248_1-d2aadc7f5675e2646d4bd456023e2335-768x994.png
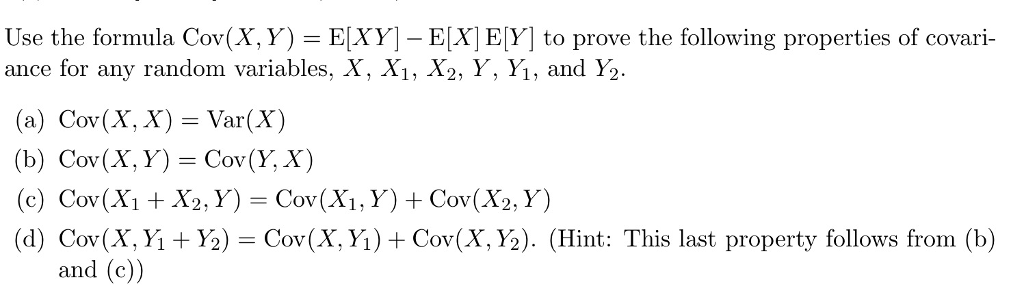
Solved Use The Formula Cov X Y E XY E X E Y To Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/c11/c116e1a3-4508-4a43-a00e-b8c1859b0d99/php5BfBOr.png

Ques 12 MCQ If E x E y E x y Then Is Teachoo
https://d1avenlh0i1xmr.cloudfront.net/bbce4bac-05a4-4441-8e54-db75799ec025/slide31.jpg
Cov X Y E X E X Y E Y As with the variance Cov X Y E XY E X E Y It follows that if X and Y are independent then E XY E X E Y and then Cov X Y 0 We know begin align Cov X Y E XY E X E Y end align Thus begin align Cov X E Y X E X cdot E Y X E X E E Y X end align As such to solve the problem we need to show
Covariance formula E XY E X E Y or expectation of product minus product of expectations is frequently useful Note if X and Y are independent then Cov X Y 0 We will start with the de nition of covariance Cov X Y E X E X Y E Y By LOTUS we know this is equal to where X E X and Y E Y X x X y x X y Y p X Y x y Intuitively we can
More picture related to show that cov x y e xy e x e y
Solved 2 Proof That Cov X U 0 With Exogeneity 25 Chegg
https://media.cheggcdn.com/media/76e/76e84b01-e2b7-4faf-8d62-458bd9f0ff21/php6COV4u

Solved 1 Let Cov X Y E XY E x E Y Denote The Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/c61/c6168429-8bf5-4c26-a488-f5779f314682/phpmApuuM.png

XX Vs XY Features Critic Te rohi
http://critic.co.nz/files/article-2463.jpg
begingroup First observe that it suffices to prove Cov X Y Cov X E Y X for X Y with E X E Y 0 Now can you prove this endgroup It is generally simpler to find the covariance by taking begin align text Cov X Y E XY E X Y X E Y E X E Y boxed E XY E X E Y end align In other words to
The covariance of two square integrable random variables X and Y is denoted by cov X Y andis de ned by cov X Y E X E X Y E Y When cov X Y 0 wesay that X and Y are To show this set g X X E X and h Y Y E Y then Cov X Y E X E X Y E Y E X E X E Y E Y 0 However if X and Y are uncorrelated they are not necessarily
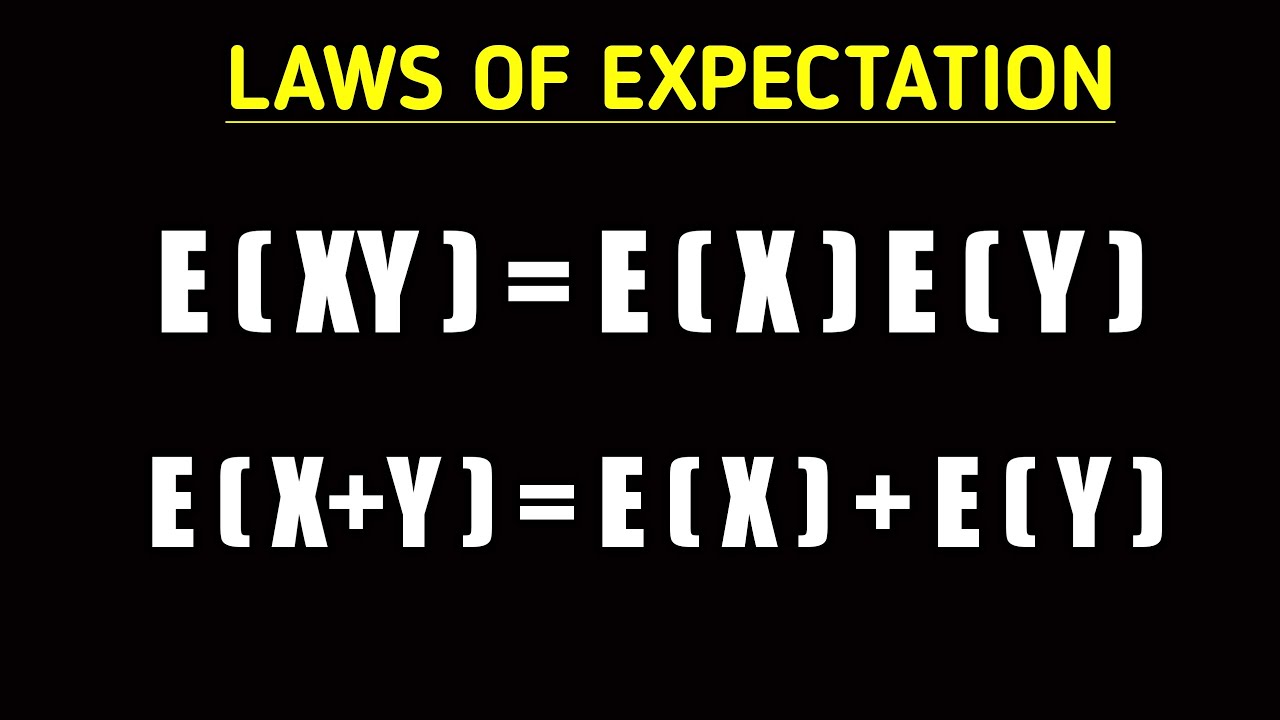
E XY E X E Y Laws Of Expectation YouTube
https://i.ytimg.com/vi/rQFW6VDBBwc/maxresdefault.jpg

Independent Random Variables Proof E g x H y I J Yhxg Ii
https://d20ohkaloyme4g.cloudfront.net/img/document_thumbnails/7e48dac9390a8e08026fd65efaaa9046/thumb_1200_1553.png
show that cov x y e xy e x e y - De nition Let X and Y be any random variables The covariance between X and Y is given by cov X Y E n X X Y Y o E XY E X E Y where X E X Y E Y 1