logarithmic equation rules

logarithmic equation rules Logarithm product rule log b x y log b x log b y Logarithm quotient rule log b x y log b x log b y Logarithm power rule log b x y y log b x Logarithm base switch rule log b c 1 log c b Logarithm base change rule log b x log c x log c b Derivative of logarithm f x log b x f

Logarithm Rules and Properties There are certain rules based on which logarithmic operations can be performed The names of these rules are Product rule Division rule Power rule Exponential Rule Change of base rule Base switch rule Derivative of log Integral of log Let us have a look at each of these properties one by one Product Rule Learn how to solve logarithmic equations in two 2 ways One way by setting the argument equal to each other and the other way by converting it as an exponential

logarithmic equation rules

logarithmic equation rules
https://i.pinimg.com/originals/49/6d/30/496d30f07aa97212cbf72f5d80e245fa.jpg

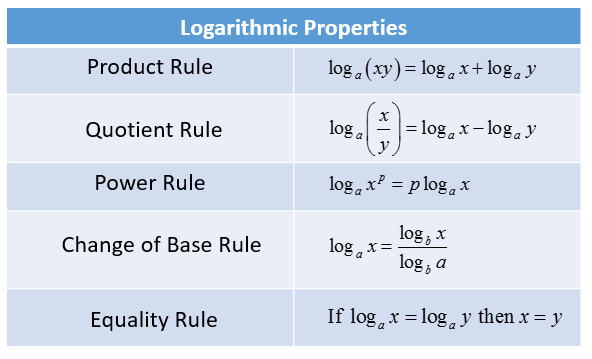
Logarithms Product Rule solutions Examples Videos Worksheets
https://www.onlinemathlearning.com/image-files/xlog-properties.png.pagespeed.ic.jdluEPfKKX.png

Logarithmic Equations YouTube
https://i.ytimg.com/vi/PIx0Z0LqqFY/maxresdefault.jpg

Basic rules for logarithms Since taking a logarithm is the opposite of exponentiation more precisely the logarithmic function log b x is the inverse function of the exponential function b x we can derive the basic rules for logarithms from the basic rules for exponents 1 Product Rule Multiplication inside the log can be turned into addition outside the log and vice versa 2 Quotient Rule Division inside the log can be turned into subtraction outside the log and vice versa 3 Power Rule An exponent on everything inside a log can be moved out front as a multiplier and vice versa

Logarithmic Equations We have already seen that every logarithmic equation logb x y l o g b x y is equal to the exponential equation by x b y x We can use this fact along with the rules of logarithms to solve logarithmic equations where the argument is an algebraic expression In this lesson we will prove three logarithm properties the product rule the quotient rule and the power rule Before we begin let s recall a useful fact that will help us along the way log b b c c In other words a logarithm in base b reverses the effect of a base b power Why is this true again log b a b a log b b c b b c c

More picture related to logarithmic equation rules

Solving Logarithmic Equations Equations Solving Organic Chemistry Tutor
https://i.pinimg.com/originals/4b/a6/20/4ba6205af226232a547adcc4e2b14c79.jpg

Solve Exponential Equation Using Natural Logarithms YouTube
https://i.ytimg.com/vi/uxBh1qY90B8/maxresdefault.jpg

Question Video Solving Logarithmic Equations Involving Laws Of
https://media.nagwa.com/292193891306/en/thumbnail_l.jpeg

Log b a c b c a Both equations describe the same relationship between a b and c b is the base c is the exponent and a is called the argument A helpful note A logarithm is the inverse of the exponential function Specifically a logarithm is the power to which a number the base must be raised to produce a given number For example log 2 64 6 because 2 6 64 In general we have the following definition z is the base x logarithm of y if and only if x z y

Discover the link between exponential function b M and log M N in this article about Logarithms Explained Understanding this basic idea helps us solve algebra problems that require switching between logarithmic and exponential forms The rules of logs are the same for all logarithms including the natural logarithm Hence the important natural log rules rules of ln are as follows ln mn ln m ln n ln m n ln m ln n ln m n n ln m ln a log a log e ln e 1 ln 1 0 The number raised to log rule mentioned in the above table is b log b x x

Transforming Exponential And Logarithmic Functions
https://s3.studylib.net/store/data/008115739_1-da95418e003b2adf96cd6e467a72bf05.png

Can You Solve Logarithmic Equations With Different Bases Easy Step
https://i.ytimg.com/vi/uhI4JrlZiR4/maxresdefault.jpg

logarithmic equation rules - Intro to logarithm properties 1 of 2 Intro to logarithm properties 2 of 2 Intro to logarithm properties Using the logarithmic product rule Using the logarithmic power rule Using the properties of logarithms multiple steps Proof of the logarithm product rule Proof of the logarithm quotient and power rules