integration of all trigonometric functions Functions consisting of products of powers of trigonometric functions of An overwhelming number of combinations of trigonometric functions can appear in these integrals but fortunately most fall into a few general patterns and most can be integrated using reduction formulas and integral tables This section examines some of these
In these cases we can use trigonometric product to sum identities cos A cos B frac 1 2 big cos A B cos A B big and likewise for the other two Find the integral In this section we look at integrals that involve trig functions In particular we concentrate integrating products of sines and cosines as well as products of secants and tangents We will also briefly look at how to modify the work for products of these trig functions for some quotients of trig functions
integration of all trigonometric functions

integration of all trigonometric functions
https://trigidentities.net/wp-content/uploads/2020/06/integration-formulas-5-791x1024.jpg

21 3 Integrals Involving Single Trigonometric Functions
https://math.mit.edu/~djk/18_01/chapter21/equations/section03_eq01.gif

Inverse Trig Integrals Integrals Of Inverse Trig Functions
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/integrals-of-inverse-trig-functions-1648121371.png
Compute the following integrals using the guidelines for integrating powers of trigonometric functions Use a CAS to check the solutions Note Some of the problems may be done using techniques of integration learned previously The six basic formulas for integration involving trigonometric functions are stated in terms of appropriate pairs of functions An integral involving sin x sin x and tan x tan x which the simple integration formula cannot be applied we must put the integrand entirely in terms of sin x sin
In this section we look at how to integrate a variety of products of trigonometric functions These integrals are called trigonometric integrals They are an important part of the integration technique called trigonometric substitution which is featured in Trigonometric Substitution This technique allows us to convert algebraic Our strategy for evaluating these integrals is to use the identity cos 2x sin 2x 1 to convert high powers of one trigonometric function into the other leaving a single sine or cosine term in the integrand We summarize the general technique in the following Key Idea
More picture related to integration of all trigonometric functions

Antiderivatives And Indefinite Integration Including Trig Integration
http://www.shelovesmath.com/wp-content/uploads/2016/06/Trigonometry-Integration-Rules.jpg

Integration Formula For Trigonometry Function
https://trigidentities.net/wp-content/uploads/2020/06/integration-formulas-2-1583x2048.jpg

Integration Of Trigonometry Functions Smtutor Learning Center Home
https://i.pinimg.com/736x/a9/e3/37/a9e3375373b76d197bbf800956689204.jpg
Integrals of polynomials of the trigonometric functions sin x text cos x text tan x and so on are generally evaluated by using a combination of simple substitutions and trigonometric identities We ll cover the essential integration formulas for trigonometric functions work through examples of integrating both indefinite and definite integrals and demonstrate how to apply trigonometric identities to simplify your solutions
[desc-10] [desc-11]

Integration Formula For Trigonometry Function
https://trigidentities.net/wp-content/uploads/2020/06/integration-formulas-4-1583x2048.jpg
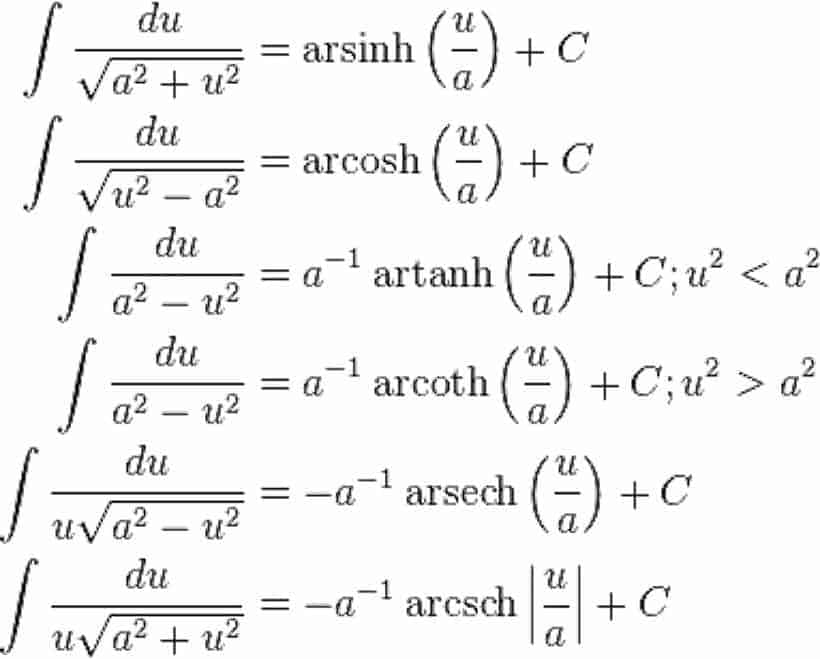
Integral Table Trigonometric Functions
https://mathvault.ca/wp-content/uploads/trig-integrals.jpg
integration of all trigonometric functions - [desc-13]