integral of e examples Exponential functions can be integrated using the following formulas exdx ex C axdx ax lna C e x d x e x C a x d x a x ln a C The nature of the antiderivative of ex e x makes it fairly easy to identify what to choose as u u If only one e e exists choose the exponent of e e as u u
Although the derivative represents a rate of change or a growth rate the integral represents the total change or the total growth Let s look at an example in which integration of an exponential function solves a common business application What is the Integral of e e is a constant Thus we can write the integral of e as e dx e 1 dx Here 1 dx x and so e dx ex C What is the Value of the Integral of e x 2 We know that e dx 2 erf x C Thus e dx e dx e ix dx Now let ix u then i dx du or dx
integral of e examples

integral of e examples
https://i.ytimg.com/vi/pkOJSDx7cKg/maxresdefault.jpg

Indefinite Integral Of X 8 5 x Calculus Integration By Parts
https://i.pinimg.com/originals/d1/87/7e/d1877e105655415bd464d302b0214d67.jpg

Example 8 i Find The Integral Dx X 2 16 Teachoo
https://d77da31580fbc8944c00-52b01ccbcfe56047120eec75d9cb2cbd.ssl.cf6.rackcdn.com/352eec24-acd3-470f-9d20-989a41c2bf9e/slide40.jpg
The following problems involve the integration of exponential functions We will assume knowledge of the following well known differentiation formulas where and where a is any positive constant not equal to 1 and is the natural base e logarithm of a These formulas lead immediately to the following indefinite integrals y int sqrt e x 3 dx and subsitute our given conditions to find the equation of the curve Put u x 3 then du dx Perform the integral y intsqrt e x 3 dx intsqrt e u du inte u 2 du 2e u 2 K 2e x 3 2 K Now the curve passes through 1 0 This means when x 1 y 0 So 0 2e 2 K giving K
Example 4 int e xe e x dx nonumber Solution For this integral we can use u substitution with u e x du e x dx nonumber The integrals becomes begin align int e u du e u C e e x C end align This integral can be solved by a substitution u x du dx du dx So now we can substitute e xdx eu du eudu eu C and substitute back e x C For simple looking integrands you should try a quick check to see if substitution works before trying harder integration methods Amory W Aug 20 2014
More picture related to integral of e examples
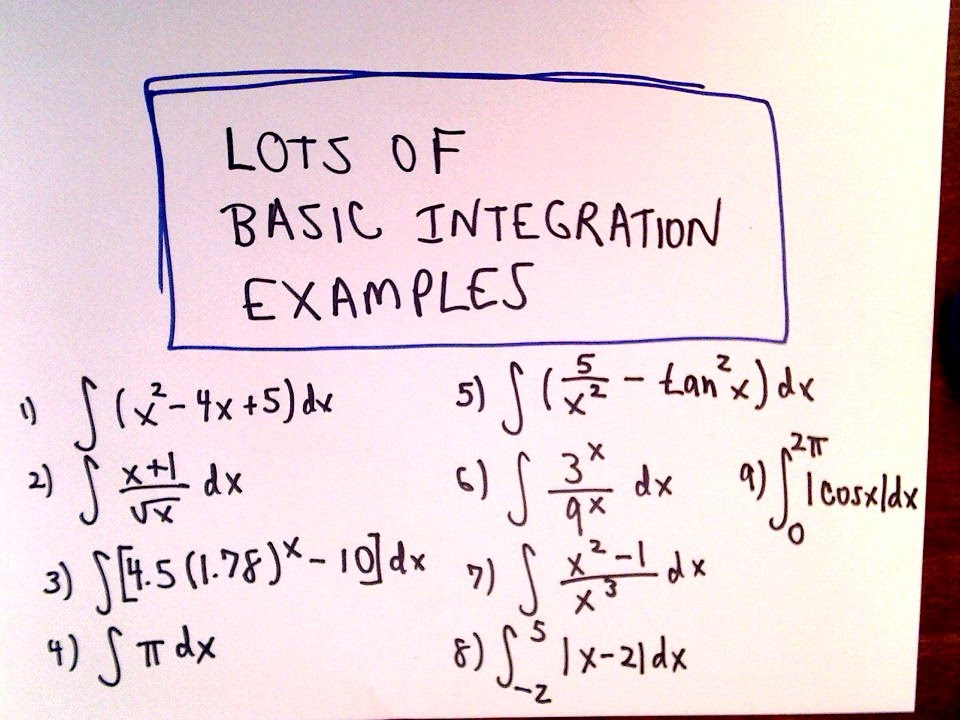
Lots Of Basic Antiderivative Integration Integral Examples YouTube
https://i.ytimg.com/vi/qAj-XzR3jOk/maxresdefault.jpg
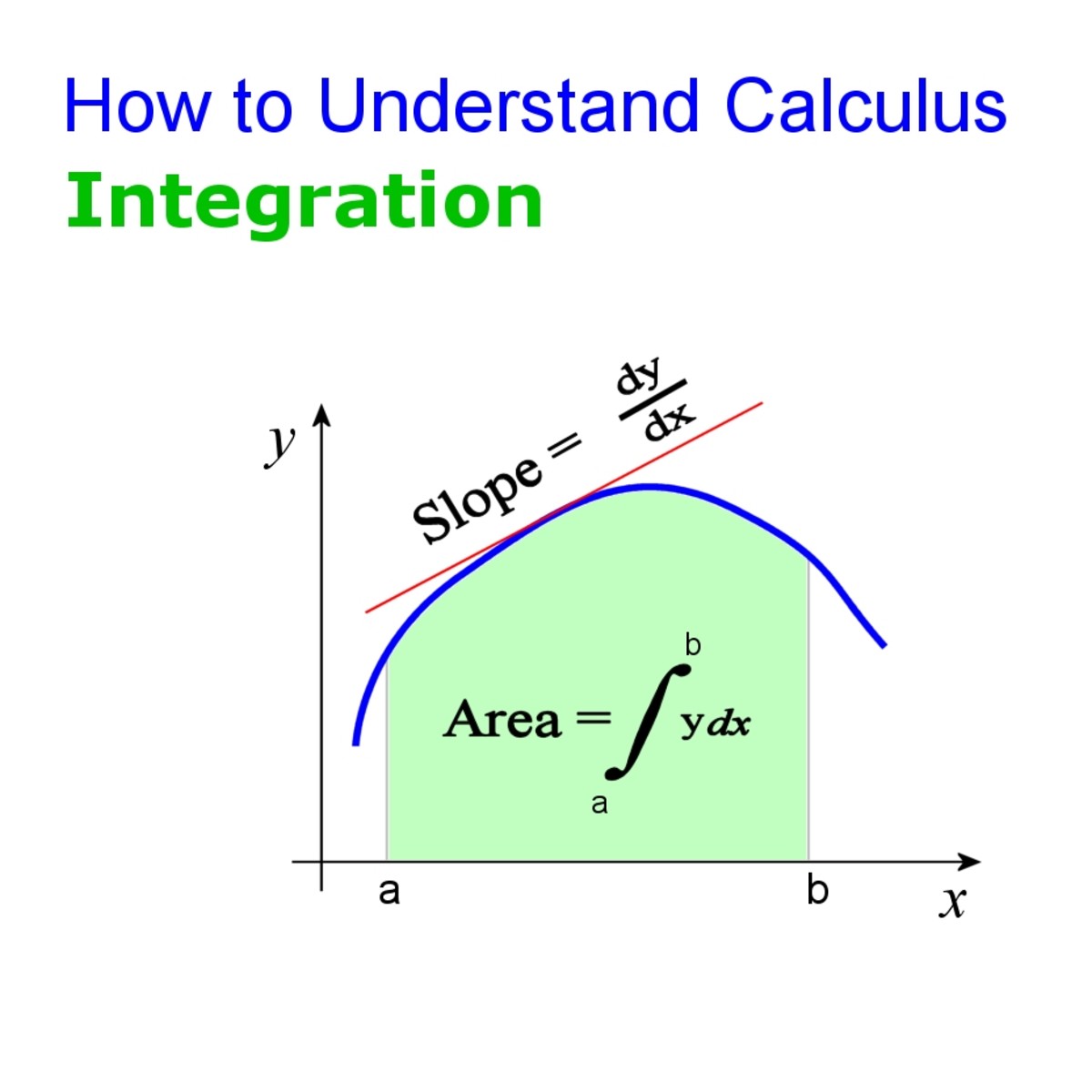
What Is Calculus Integration Rules And Examples Owlcation
https://usercontent1.hubstatic.com/14560796_f1024.jpg

Solved Integrals With E x Evaluate The Following Integrals Chegg
https://d2vlcm61l7u1fs.cloudfront.net/media/131/131d3821-ef1e-4890-bcb7-242b1eb91643/phpV7PU0M.png
Bookshelves Calculus OpenStax 6 Applications of Integration Expand collapse global location 6 7 Integrals Exponential Functions and Logarithms Page ID Gilbert Strang Edwin Jed Herman OpenStax Learning Objectives Write the definition of the natural logarithm as an integral Recognize the derivative of the natural logarithm Its integral is I dfrac e ax big a cos bx c b sin bx c big a 2 b 2 I a2 b2eax acos bx c bsin bx c We ll integrate the above using integration by parts as follows
[desc-10] [desc-11]

How To Find The Integral Of A Function Perkins Thoposel
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/integration-formula-1641294788.png

Definite Integral YouTube
https://i.ytimg.com/vi/Gc3QvUB0PkI/maxresdefault.jpg
integral of e examples - y int sqrt e x 3 dx and subsitute our given conditions to find the equation of the curve Put u x 3 then du dx Perform the integral y intsqrt e x 3 dx intsqrt e u du inte u 2 du 2e u 2 K 2e x 3 2 K Now the curve passes through 1 0 This means when x 1 y 0 So 0 2e 2 K giving K