integral of divergence is zero Note that the flux integral here would be over a complicated surface over dozens of rectangular planar regions h 2 cos cos 2 cos sin sin i Solution The answer is
One classic condition is that V vanishes at infinity in which case the integral of divergence is zero by Stokes s Theorem If F has the form F f y z g x z h x y F f y z g x z h x y then the divergence of F is zero By the divergence theorem the flux of F across S is also zero This makes certain flux integrals incredibly easy to
integral of divergence is zero

integral of divergence is zero
https://media.cheggcdn.com/media/260/26095aaf-a368-4e1f-a0b1-9d4c0092d17b/phpSNFqsX.png
Function Continuous At X 2 And X 5 But Integral Is Divergent Campbell
https://www.sfu.ca/math-coursenotes/Math 158 Course Notes/images/improper-integral-theory-2.svg

Question Video Determining Whether The Integrals Of Trigonometric
https://media.nagwa.com/794192471983/en/thumbnail_l.jpeg
As the name implies the divergence is a local measure of the degree to which vectors in the field diverge The divergence of a tensor field of non zero order k is written as a contraction of a tensor field of order k 1 Specifically the Divergence Theorem Let be a closed surface in R3 which bounds a solid S and let f x y z f1 x y z i f2 x y z j f3 x y z k be a vector field defined on some subset of R3 that contains Then f d
Solution The answer is 0 because the divergence of curl F is zero By the divergence theorem the ux is zero If F has the form F f y z g x z h x y then the divergence of F is zero By the divergence theorem the flux of F across S is also zero This makes certain flux integrals incredibly easy to calculate For example suppose we wanted
More picture related to integral of divergence is zero

Why Divergence Of Magnetic Field Is Zero Divergence Of Magnetic
https://i.ytimg.com/vi/VMyk7gD31oc/maxresdefault.jpg
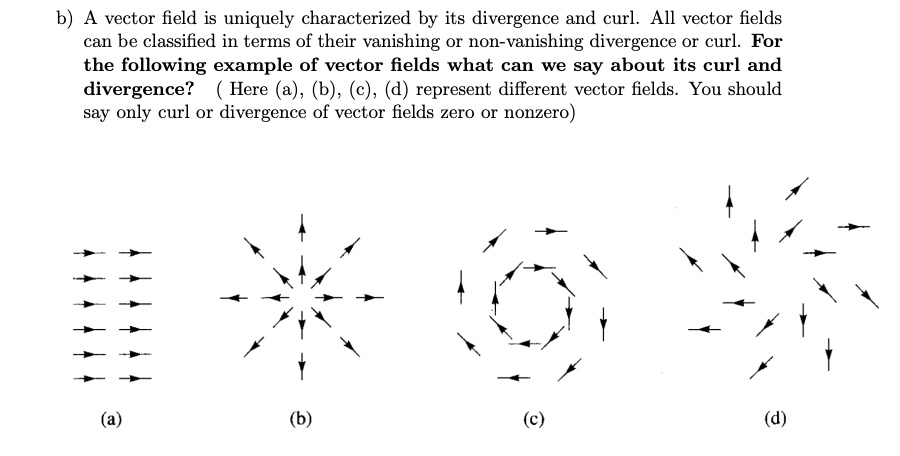
SOLVED B Vector Field Is Uniquely Characterized By Its Divergence And
https://cdn.numerade.com/ask_images/d8eca052f1204bfea380ee60848c4d92.jpg

The Divergence Theorem Part 1 YouTube
https://i.ytimg.com/vi/jJHta6WfzEQ/maxresdefault.jpg
F across S1by using the divergence theorem to relate it to the flux across S2 Solution We see immediately that div F 0 Therefore if we let Si be the same surface as S2 but oppositely Like the fundamental theorem of calculus the divergence theorem expresses the integral of a derivative of a function in this case a vector valued function over a region in terms of the values of the function on the boundary
Now if the vector FLPC is everywhere finite the line integral around Gamma must go to zero as we shrink the loop the integral is roughly proportional to the circumference of Divergence Theorem Di R3 fdVi Di R2 f nidSi i N 1 The volume integral over some domain D of the divergence of a vector f equals the surface integral of the

Calculus 2 Integral Test For Convergence And Divergence Of Series
https://i.ytimg.com/vi/f9SJz4-UaQQ/maxresdefault.jpg

Ex Use The Divergence Theorem To Evaluate A Flux Integral Spherical
https://i.ytimg.com/vi/BVAbztfd2JM/maxresdefault.jpg
integral of divergence is zero - As the name implies the divergence is a local measure of the degree to which vectors in the field diverge The divergence of a tensor field of non zero order k is written as a contraction of a tensor field of order k 1 Specifically the
