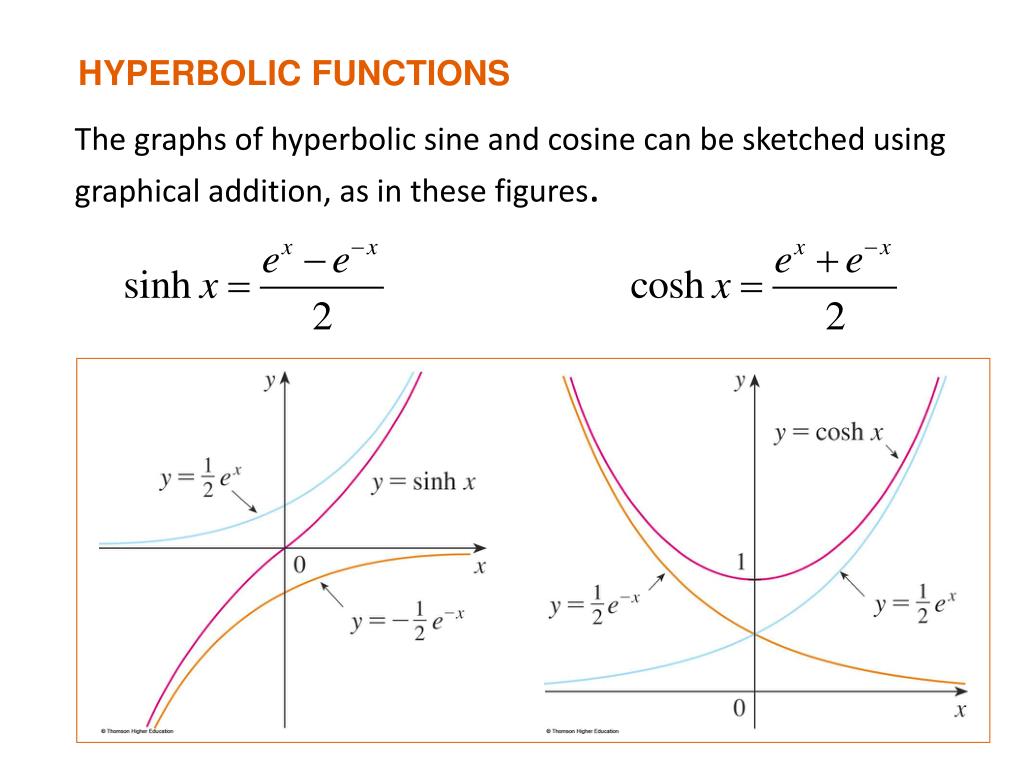
hyperbolic cosine function The two basic hyperbolic functions are sinh and cosh Hyperbolic Sine sinh x e x e x 2 pronounced shine Hyperbolic Cosine cosh x e x e x 2 pronounced cosh They use the natural exponential function e x And are not the same as sin x and cos x but a little bit similar sinh vs sin cosh vs cos Catenary
The hyperbolic cosine is defined as coshz 1 2 e z e z 1 The notation chx is sometimes also used Gradshteyn and Ryzhik 2000 p xxix This function describes the shape of a hanging cable known as the catenary It is implemented in the Wolfram Language as Cosh z Hyperbolic Cosine Function The hyperbolic cosine function is a function f R R is defined by f x e x e x 2 and it is denoted by cosh x cosh x ex e x 2 Graph y cosh x Hyperbolic Tangent Function
hyperbolic cosine function

hyperbolic cosine function
https://i.stack.imgur.com/jGn1w.png

The Hyperbolic Trigonometric Functions Extend The Notion Of The
https://i.pinimg.com/originals/f8/55/62/f855620facf3bf541d8b0439b9a91b19.png

Hyperbolic Functions solutions Examples Videos
https://www.onlinemathlearning.com/image-files/xhyperbolic-functions.png.pagespeed.ic.Ma23JVGDCf.png
The hyperbolic trigonometric functions extend the notion of the parametric equations for a unit circle x cos t x cost and y sin t y sint to the parametric equations for a hyperbola which yield the following two fundamental hyperbolic equations x cosh a dfrac e a e a 2 quad y sinh a dfrac e a e a 2 Hyperbolic functions can be used to model catenaries Specifically functions of the form y a cdot cosh x a are catenaries Figure PageIndex 4 shows the graph of y 2 cosh x 2 Figure PageIndex 4 A hyperbolic cosine
The hyperbolic cosine function is an old mathematical function It was used in the works of V Riccati 1757 D Foncenex 1759 and J H Lambert 1768 This function is easily defined as the half sum of two exponential functions in the points and The hyperbolic cosine function is the shape of a hanging cable the so called catenary The hyperbolic tangent arises in the calculation of and rapidity of special relativity All three appear in the Schwarzschild metric using external isotropic Kruskal coordinates in general relativity
More picture related to hyperbolic cosine function

PPT Hyperbolic FUNCTIONS PowerPoint Presentation Free Download ID
https://image2.slideserve.com/3997128/slide5-l.jpg

Hyperbolic Functions HubPages
https://usercontent1.hubstatic.com/271102_f520.jpg
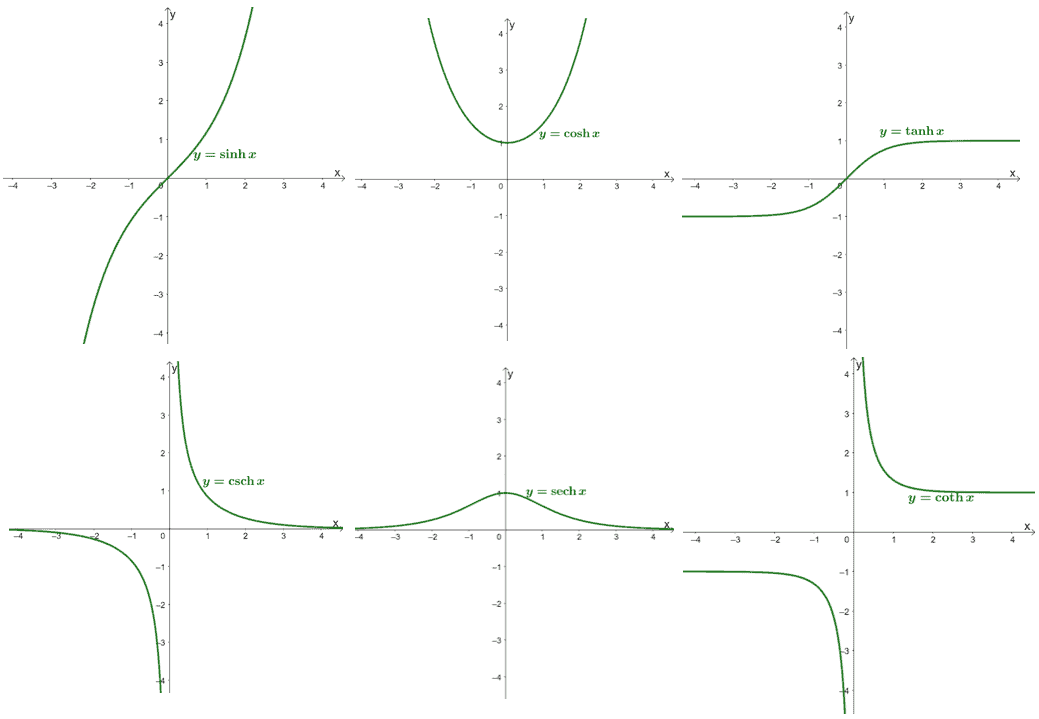
Integration Of Hyperbolic Functions Definition Formulas And Examples
https://www.storyofmathematics.com/wp-content/uploads/2021/05/graphs-of-six-hyperbolic-functions.png
These functions arise naturally in various engineering and physics applications including the study of water waves and vibrations of elastic membranes Another common use at least for the hyperbolic cosine is the representation of a hanging chain or cable also known as a catenary Figure 1 7 5 Definition 4 11 1 Hyperbolic Cosines and Sines The hyperbolic cosine is the function coshx ex e x 2 and the hyperbolic sine is the function sinhx ex e x 2
Proof The proof is a straightforward computation cosh2x sinh2x ex e x 2 4 ex e x 2 4 e2x 2 e 2x e2x 2 e 2x 4 4 4 1 This immediately gives two additional identities 1 tanh2x sech2x and coth2x 1 csch2x The identity of the theorem also helps to provide a geometric motivation The hyperbolic cosine function calculates the hyperbolic cosine of an angle It is an example of a hyperbolic trigonometric function which has measures based on the hyperbola instead of the unit circle which is the basis for the usual trigonometric functions

PPT Hyperbolic FUNCTIONS PowerPoint Presentation Free Download ID
https://image2.slideserve.com/3997128/slide4-l.jpg
PPT Hyperbolic FUNCTIONS PowerPoint Presentation Free Download ID
https://image2.slideserve.com/3997128/slide7-l.jpg
hyperbolic cosine function - Hyperbolic functions the hyperbolic sine of z written sinh z the hyperbolic cosine of z cosh z the hyperbolic tangent of z tanh z and the hyperbolic cosecant secant and cotangent of z