how to find maximum and minimum point A high point is called a maximum plural maxima A low point is called a minimum plural minima The general word for maximum or minimum is extremum plural extrema We say local maximum or minimum when there may be higher or lower points elsewhere but not nearby
Local Maximum First we need to choose an interval Then we can say that a local maximum is the point where The height of the function at a is greater than or equal to the height anywhere else in that interval Or more briefly f a f x for all x in the interval You can find the maximum or minimum if your original function is written in general form or in standard form Finally you may also wish to use some basic calculus to define the maximum or minimum of any quadratic function
how to find maximum and minimum point

how to find maximum and minimum point
http://spmaddmaths.blog.onlinetuition.com.my/wp-content/uploads/sites/3/2013/05/Picture8.png
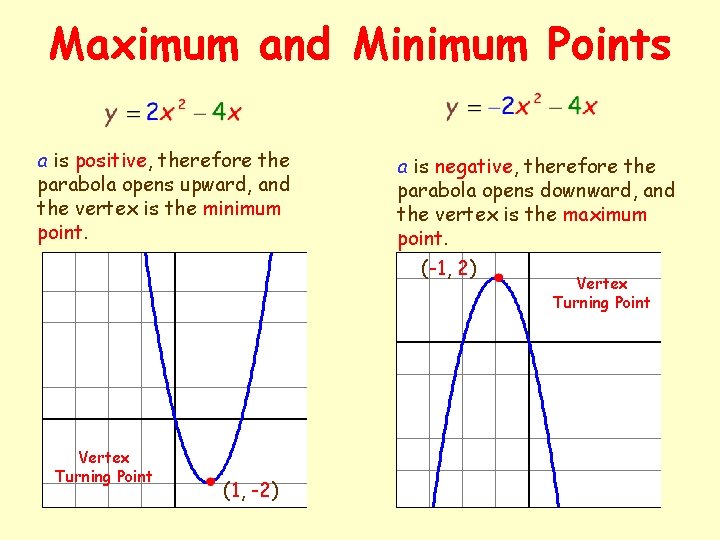
How To Calculate Maximum And Minimum Point Of A Function PELAJARAN
https://slidetodoc.com/presentation_image_h/ea0270886404a738801b2d788e34cbf2/image-2.jpg

3 4 Finding The Maximum And Minimum Points Of Quadratic Function Using
https://spmaddmaths.blog.onlinetuition.com.my/wp-content/uploads/sites/3/2013/05/Picture5.png
The following steps would be useful to find the maximum and minimum value of a function using first and second derivatives Step 1 Let f x f x be a function Find the first derivative of f x which is f x Step 2 Equate the first derivative f x to zero and solve for x which are called critical numbers Step 3 Find the absolute maximum and absolute minimum of f x x 2 4x 3 over the interval 1 4 Hint Look for critical points Evaluate f at all critical points and at the endpoints Answer The absolute maximum is 3 and it occurs at x 4 The absolute minimum is 1 and it occurs at x 2
The point x 0 y 0 underneath a peak in the input space which in this case means the x y plane is called a local maximum point The output of a function at a local maximum point which you can visualize as the height of the graph above that point is the local maximum itself Derivative tests are the quickest ways to find the maxima and minima of a function
More picture related to how to find maximum and minimum point

How To Find Maximum And Minimum Values On A Graph Images And Photos
https://www.wikihow.com/images/3/37/Find-the-Maximum-or-Minimum-Value-of-a-Quadratic-Function-Easily-Step-15-Version-3.jpg

Quadratic Functions Page 2 User s Blog
http://spmaddmaths.blog.onlinetuition.com.my/wp-content/uploads/sites/3/2013/05/Picture6.png

Absolute Maximum Minimum For Polynomial YouTube
https://i.ytimg.com/vi/2J74DATf29w/maxresdefault.jpg
Definition We say that f x f x has an absolute or global maximum at x c x c if f x f c f x f c for every x x in the domain we are working on We say that f x f x has a relative or local maximum at x c x c if f x f c f x f c for every x x in some open interval around x c x c How do I find absolute minimum maximum points with differential calculus An absolute maximum point is a point where the function obtains its greatest possible value Similarly an absolute minimum point is a point where the function obtains its least possible value
[desc-10] [desc-11]

Maximum Point Minimum Point Turning Point Of A Curve YouTube
https://i.ytimg.com/vi/KWnnVy3ff_Q/maxresdefault.jpg

3 4 1 Example 1 Finding The Maximum And Minimum Points Of Quadratic
http://spmaddmaths.blog.onlinetuition.com.my/wp-content/uploads/sites/3/2013/05/Picture9.png
how to find maximum and minimum point - [desc-14]