how to factor polynomials So factor the polynomial in u s then back substitute using the fact that we know u x 2 begin align x 4 x 2 20 u 2 u 20 left u 4 right left u 5 right left x 2 4 right left x 2 5 right end align
To factor the GCF out of a polynomial we do the following Find the GCF of all the terms in the polynomial Express each term as a product of the GCF and another factor Use the distributive property to factor out the GCF Let s factor the GCF out of 2 x 3 6 x 2 Step 1 Find the GCF 2 x 3 2 x x x Let s get equipped with a variety of key strategies for breaking down higher degree polynomials From taking out common factors to using special products we ll build a strong foundation to help us investigate polynomial functions and prove identities
how to factor polynomials

how to factor polynomials
https://maliarivera.com/wp-content/uploads/2021/05/factoring-polynomials-by-grouping-graphic-1365x2048.jpg

How To Factor Polynomials Step by Step Mashup Math
https://images.squarespace-cdn.com/content/v1/54905286e4b050812345644c/1414914a-3fa8-4e5e-97a4-76603244be19/FIgure-01.jpg
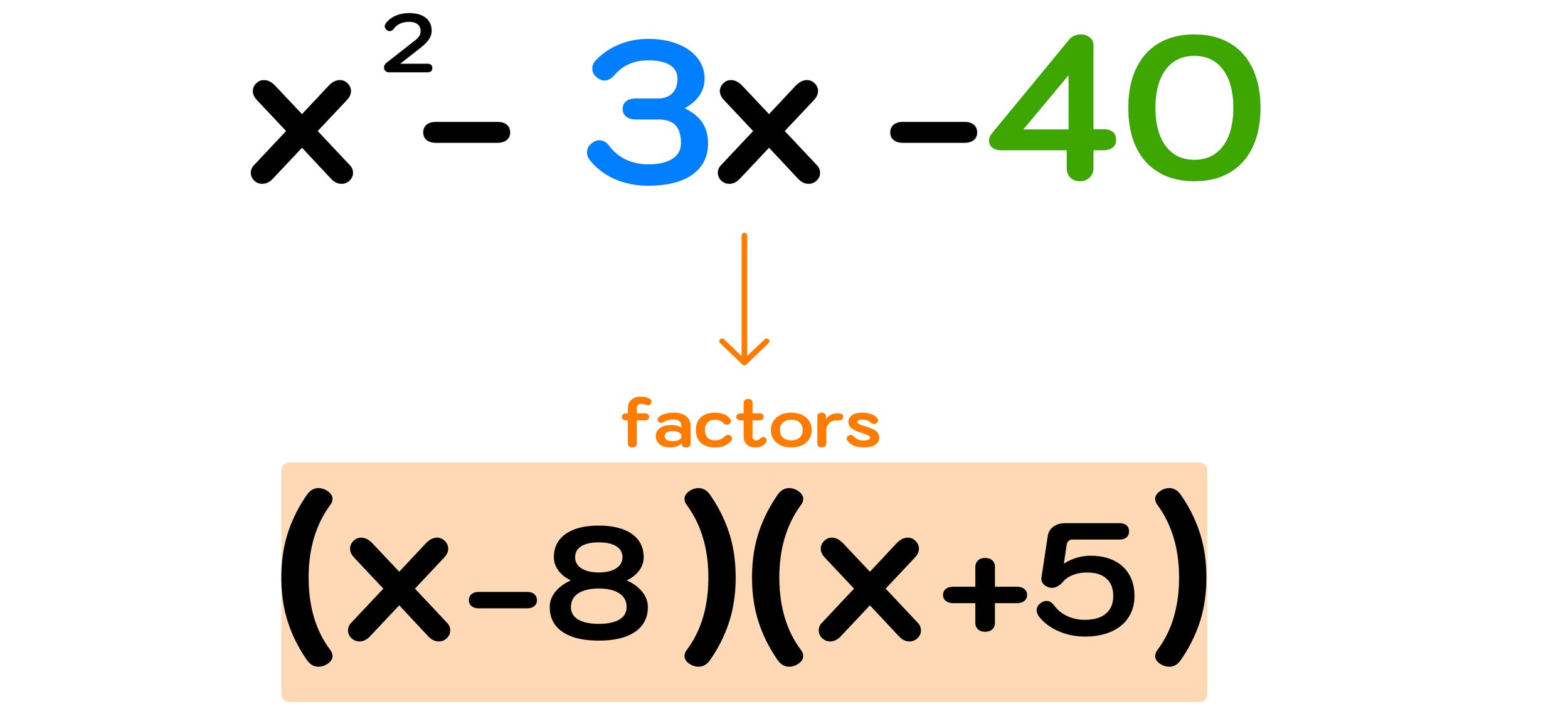
How To Factor Polynomials Step by Step Mashup Math
https://images.squarespace-cdn.com/content/v1/54905286e4b050812345644c/033fc137-440e-4b1f-acac-7bc061ff641d/Fig09.jpg
Yes there are several methods to solve higher degree polynomials polynomials of degree three or higher other than grouping The most common methods include 1 Factoring This method involves factoring the polynomial into simpler expressions that can be set to zero to find the roots solutions To factor out the GCF of a polynomial we first determine the GCF of all of its terms Then we can divide each term of the polynomial by this factor as a means to determine the remaining factor after applying the distributive property in reverse
We will look at 3 common ways in which a polynomial can be factored grouping substitution and using identities Contents Factoring Polynomials by Grouping Factoring by Substitution Factoring Polynomials using Identities Factoring Polynomials by Grouping We often see the grouping method applied to polynomials 1 5 Factoring Polynomials College Algebra 2e OpenStax A s2 42 16 10x 8 4 A lw 4 10x 8 40x 32 2 16 40x 32 40x 60x2 40x 20x 3x 2 4 16 20 16 20 4x 16x 20x2 16x 20x2 6x3y3 45x2y2 21xy x3 x2 xn y3 y2 3xy 2x2y2 6x3y3 3xy 15xy 45x2y2 3xy 7 21xy
More picture related to how to factor polynomials

How To Factor A Cubic Polynomial 12 Steps with Pictures
https://www.wikihow.com/images/2/2c/Factor-a-Cubic-Polynomial-Step-12.jpg

How To Factor Polynomials The Easy Way YouTube
https://i.ytimg.com/vi/U6FndtdgpcA/maxresdefault.jpg

PPT Factoring Polynomials PowerPoint Presentation Free Download ID
https://image.slideserve.com/326069/factoring-polynomials7-l.jpg
Factoring polynomials involves breaking an expression down into a product of other smaller polynomials similar to how prime factorization breaks integers down into a product of prime factors There are a number of different approaches to factoring polynomials General Strategy for Factoring Polynomials See Figure PageIndex 1 How to Factor Polynomials Is there a greatest common factor Factor it out Is the polynomial a binomial trinomial or are there more than three terms If it is a binomial Is it a sum Of squares Sums of squares do not factor Of cubes Use the sum of cubes pattern
[desc-10] [desc-11]
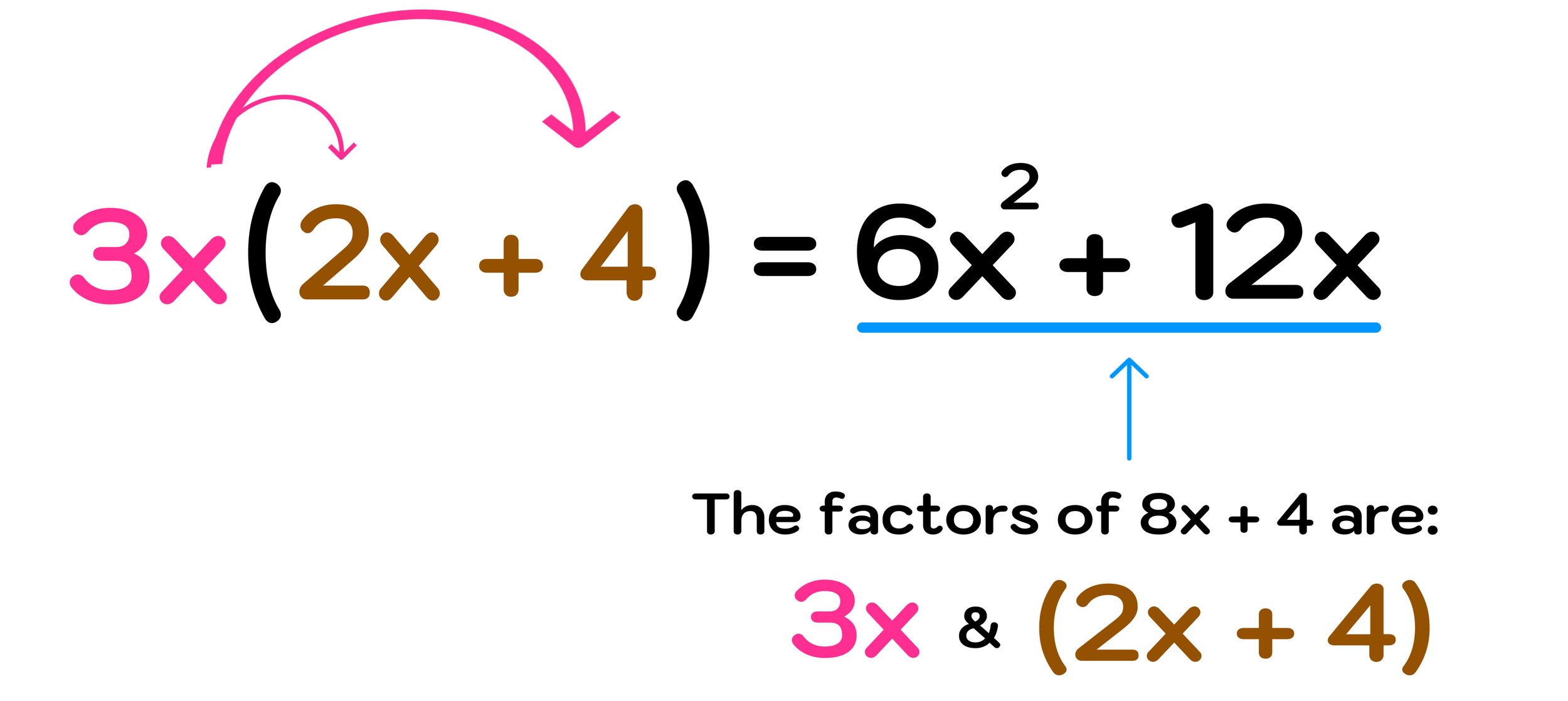
How To Factor Polynomials Step by Step Mashup Math
https://images.squarespace-cdn.com/content/v1/54905286e4b050812345644c/82cd70f3-2085-45a1-9cc3-aa0aa778c5fb/Figure-04.jpg
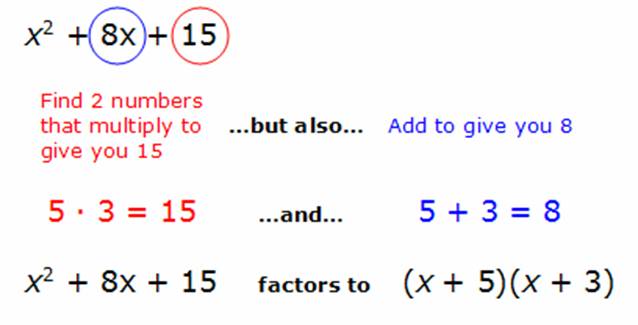
Polynomials And Factoring
http://www.gradeamathhelp.com/images/guess-check.jpg
how to factor polynomials - [desc-12]