how to expand 3 terms 458 63K views 11 years ago Binomial Theorem Expand 1 x x 2 7 in ascending powers of x up to the term in x 3 If you like what you see please subscribe to this channel youtub
Expand a term or a factor Multiply polynomials binomials trinominals and monomials with our free step by step math calculator Step 1 We have a binomial to the power of 3 so we look at the 3rd row of Pascal s triangle We have 4 terms with coefficients of 1 3 3 and 1 Step 2 a is the first term inside the bracket which is and b is the second term inside the bracket which is 2 n is the power on the brackets so n 3
how to expand 3 terms

how to expand 3 terms
https://mathsathome.com/wp-content/uploads/2021/10/example-of-binomial-expansion-1024x579.png
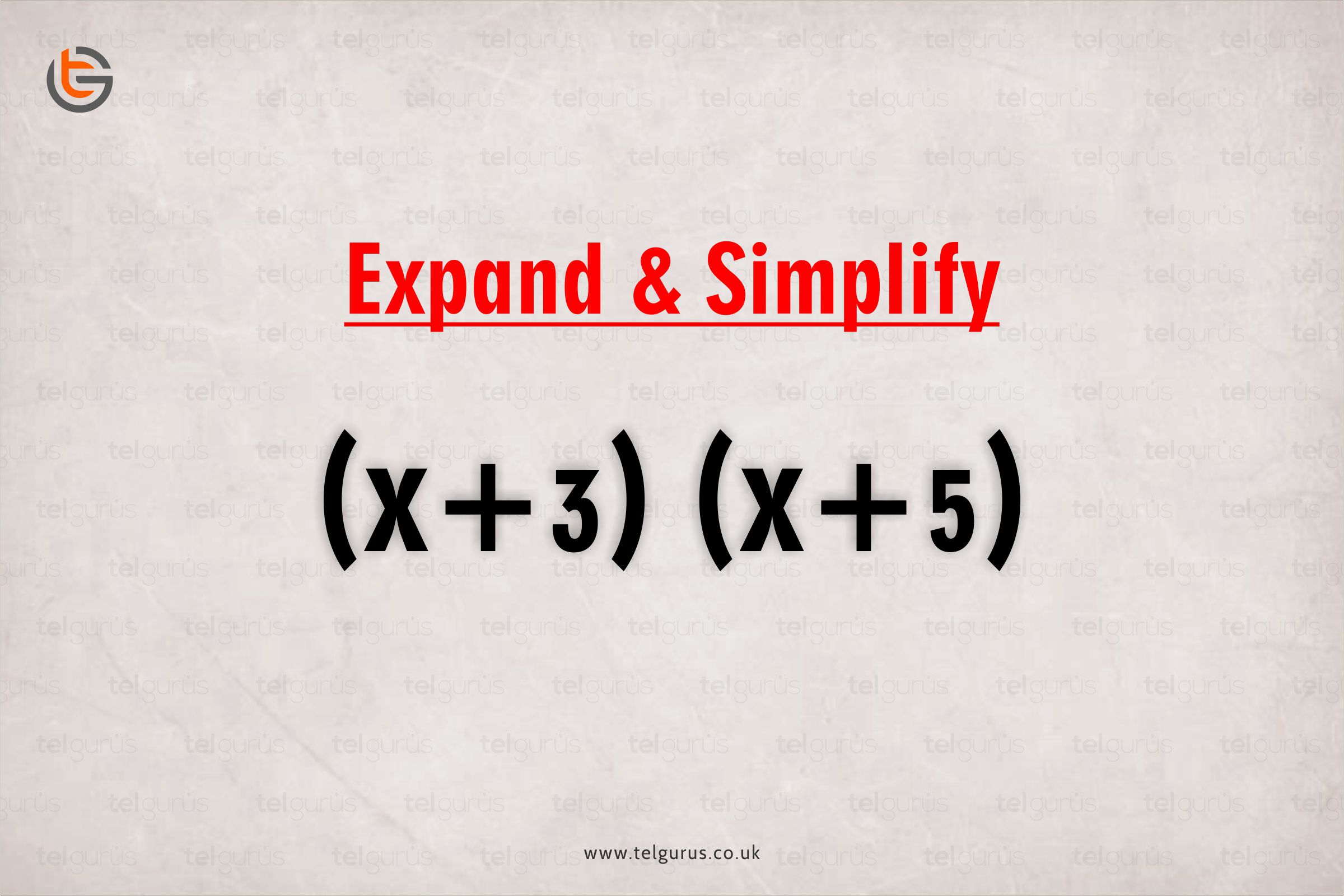
Expand And Simplify x 3 x 5 TEL Gurus
https://telgurus.co.uk/srcgurus/uploads/2022/01/x3-x5.jpg

How To Do The Binomial Expansion Mathsathome
https://mathsathome.com/wp-content/uploads/2021/10/binomial-expansion-with-a-negative-1024x578.png
It s essentially x y x y and then multiply the first terms leftmost then first term of one with last term of the other outer then second term of one with first term of other inner then the two last terms of each right most and add them up so x x x y y x y y x 2 2xy y 2 Learn all about sequences In this playlist we will explore how to write the rule for a sequence determine the nth term determine the first 5 terms or
The binomial theorem Intro to the Binomial Theorem Google Classroom About Transcript The Binomial theorem tells us how to expand expressions of the form a b for example x y The larger the power is the harder it is to expand expressions like this directly But with the Binomial theorem the process is relatively fast 1 3 3 1 for n 3 Squared term is second from the right so we get 3 1 1 x 5 2 3x 2 25 so not here 1 4 6 4 1 for n 4 Squared term is the third from the right so we get 6 1 2 x 5 2 6x 2 25 1 5 10 10 5 1 for n 5 Squared term is fourth from the right so 10 1 3 x 5 2 10x 2 25 2x 2 5 getting closer 1 6 15 20 15 6 1 for n 6
More picture related to how to expand 3 terms

Question Video Expanding Single Bracket Expressions Involving
https://media.nagwa.com/472161048589/en/thumbnail_l.jpeg

What Is The Coefficient Of The Third Term In A Binomial That Is Raised
https://mathsathome.com/wp-content/uploads/2021/10/list-of-binomial-expansion-formulae-1024x579.png

Expand 1x Y3 3 Maths Questions
https://d1hj4to4g9ba46.cloudfront.net/questions/1203630_1448224_ans_50ce05e9fa8d46d6b0ab87fc461c3951.jpg
Binomial Theorem Calculator Algebra A closer look at the Binomial Theorem The easiest way to understand the binomial theorem is to first just look at the pattern of polynomial expansions below x y 2 x 2 2xy y 2 x y 3 x 3 3x 2 y 3xy 2 y 3 x y 4 x 4 4x 3 y 6x 2 y 2 4xy 3 y 4 Binomial Theorem Formula This topic covers expanding an algebraic expression involving three terms This topic covers expanding an algebraic expression involving three terms Year 10 Interactive Maths Second Edition Expanding Three Terms Example 8 Solution Alternatively We can expand as follows Home Page Order Maths Software About the Series
Algebra Expand Using the Binomial Theorem a b 3 a b 3 a b 3 Use the binomial expansion theorem to find each term The binomial theorem states a b n n k 0nCk an kbk a b n k 0 n n C k a n k b k 3 k 0 3 3 k k a 3 k b k k 0 3 3 3 k k a 3 k b k Expand the summation Answer It is now expanded We can also complete the calculation 3 5 2 3 5 3 2 15 6 21 In Algebra putting two things next to each other usually means to multiply So 3 a b means to multiply 3 by a b Here is an example of expanding using variables a b and c instead of numbers
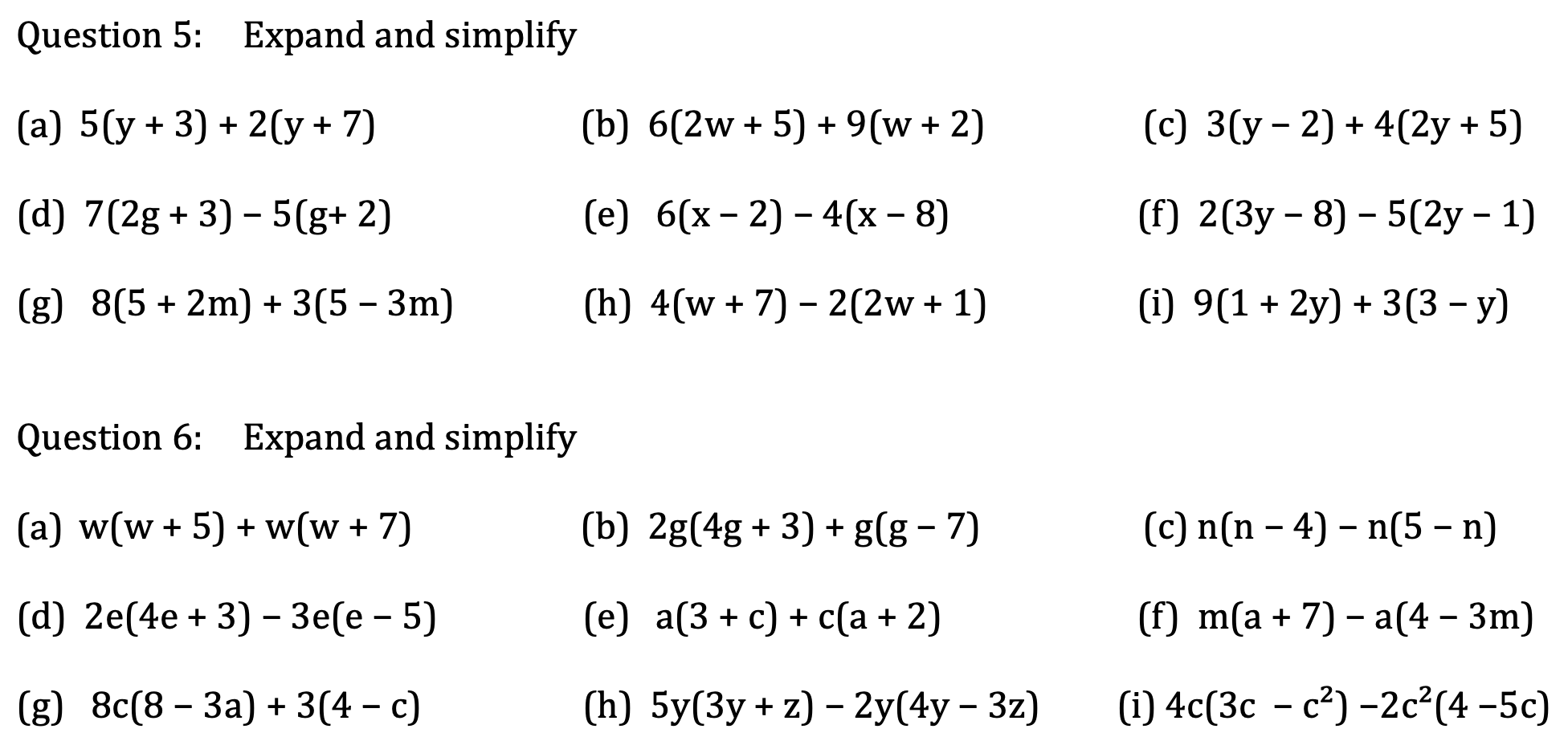
KS3 Algebra 2 Expanding Brackets Maths With David
https://mathswithdavid.files.wordpress.com/2021/04/image-269.png

2 Expand 2x 3y 5 Using Binomial Theorem YouTube
https://i.ytimg.com/vi/UahoRFTe8wo/maxresdefault.jpg
how to expand 3 terms - The perfect square rule is a technique used to expand expressions that are the sum or difference of two squares such as a b 2 or a b 2 The rule states that the square of the sum or difference of two terms is equal to the sum or difference of the squares of the terms plus twice the product of the terms Show more