how to do binomial expansion with 3 terms For three terms we can do the same thing begin align x y z x y z x x y z y x y z z x y z x 2 xy xz xy y 2 yz xz yz z 2 x 2 y 2 z 2 2xy 2xz 2yz end align Share
So you 12 terms of the form x2 22x in total 24x5 For 5 2 1 1 1 there are 4 1 3 3 4 cases and the terms are of the form x2 2x 2x 2x 8x5 in total 32x5 So the x5 term is 24x5 32x5 8x5 In your method you also need to expand 2x x2 with a binomial sum Expanding binomials video Series Khan Academy Google Classroom About Transcript Sal expands 3y 2 6x 3 5 using the binomial theorem and Pascal s triangle Created by Sal Khan Questions Tips Thanks Want to join the conversation Log in Sort by Top Voted Ed 9 years ago This problem is a bit strange to me
how to do binomial expansion with 3 terms

how to do binomial expansion with 3 terms
https://i.ytimg.com/vi/LMUGFWGXAUw/maxresdefault.jpg
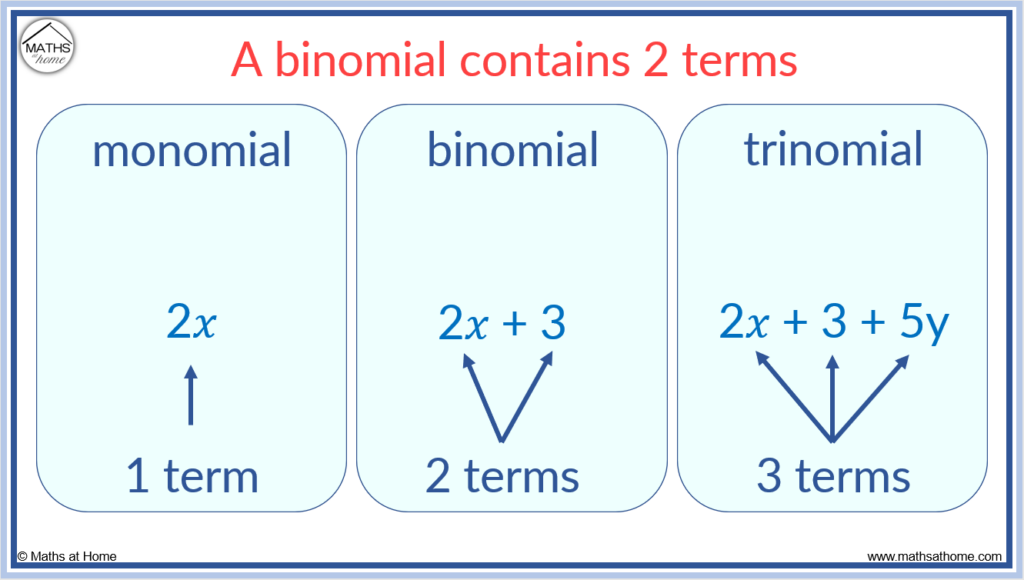
How To Do The Binomial Expansion Mathsathome
https://mathsathome.com/wp-content/uploads/2021/10/binomial-definition-1024x580.png

Question Video Finding The Coefficient Of A Certain Term In A Binomial
https://media.nagwa.com/254128151254/en/thumbnail_l.jpeg
The Binomial theorem tells us how to expand expressions of the form a b for example x y The larger the power is the harder it is to expand expressions like this directly But with the Binomial theorem the process is relatively fast Created by Sal Khan Questions Tips Thanks Want to join the conversation Log in Sort by Top Voted Let us find the fifth term in the expansion of 2x 3 9 using the binomial theorem The formula to find the n th term in the binomial expansion of x y n is T r 1 n C r x n r y r Applying this to 2x 3 9 T 5 T 4 1 9 C 4 2x 9 4
A b is a binomial the two terms are a and b Let us multiply a b by itself using Polynomial Multiplication a b a b a2 2ab b2 Now take that result and multiply by a b again a 2 2ab b 2 a b a3 3a2b 3ab2 b3 And again a 3 3a 2 b 3ab 2 b 3 a b a4 4a3b 6a2b2 4ab3 b4 As we know any k th term in the expansion of x y n is written as n C k x n k y k Here we want the term x 3 and n 4 that means n k 3 4 k 3 k 1 Thus the term with x 3 is 4 C 1 2x 4 1 5 1 4 8x 3 5 160x 3 The coefficient of x 3 is 160 More Resources Newton s Binomial Theorem
More picture related to how to do binomial expansion with 3 terms

How To Do The Binomial Expansion Mathsathome
https://mathsathome.com/wp-content/uploads/2021/10/example-of-binomial-expansion-1024x579.png

A Breakdown Of Binomial Distribution By Kulle Omer Medium
https://miro.medium.com/max/1400/1*Mj3GJfzSGrI-YpyzJWh8Tg.png

How To Do The Binomial Expansion Mathsathome
https://mathsathome.com/wp-content/uploads/2021/10/list-of-binomial-expansion-formulae-1024x579.png
The Binomial Expansions Formula will allow us to quickly find all of the terms in the expansion of any binomial raised to the power of n a b n Where n is a positive integer By the end of this section we ll know how to write all the terms in the expansions of binomials like 2 x 4 2x 3 5 4 Key Points According to the theorem it is possible to expand the power x y n x y n into a sum involving terms of the form ax by c axbyc where the exponents b b and c c are nonnegative integers with b c n b c n and the coefficient a a of each term is a specific positive integer depending on n n and b b
458 63K views 11 years ago Binomial Theorem Expand 1 x x 2 7 in ascending powers of x up to the term in x 3 If you like what you see please subscribe to this channel The sum of the exponents in each term of the expansion are 3 There are 4 terms in the 3rd degree expansion Summarizing What patterns do we need to do any binomial expansion The powers of the first term the a term descend in consecutive order starting with the power of the expansion and ending with the zero power

Using A Binomial Expansion To Approximate A Power YouTube
https://i.ytimg.com/vi/H6oM0_r5eyI/maxresdefault.jpg

23 The Binomial Theorem Binomial Expansion Part 1 YouTube
https://i.ytimg.com/vi/SwaVN0epc0w/maxresdefault.jpg
how to do binomial expansion with 3 terms - The Binomial theorem tells us how to expand expressions of the form a b for example x y The larger the power is the harder it is to expand expressions like this directly But with the Binomial theorem the process is relatively fast Created by Sal Khan Questions Tips Thanks Want to join the conversation Log in Sort by Top Voted