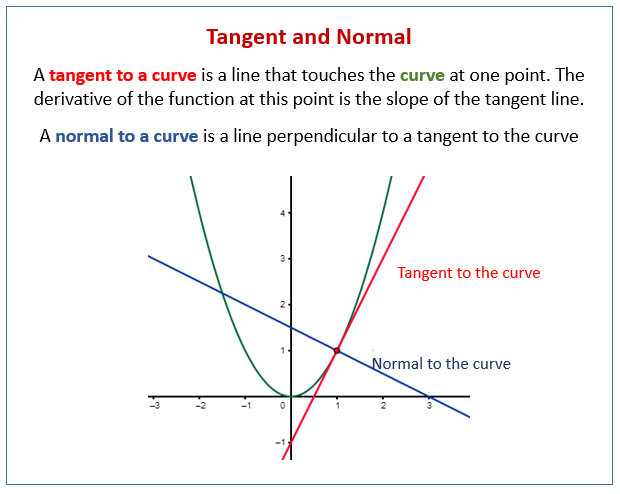
gradient of normal and tangent We learn how to find the tangent and the normal to a curve at a point along a curve using calculus The tangent has the same gradient as the curve at the point The gradient is therefore equal to the derivative at this point The normal is perpendicular to the tangent to the curve
How to Compare the Tangent and Normal Let s denote the gradient of the tangent m T and gradient of the normal m N For a pair of tangent and normal lines at one point we have one rule The two must be perpendicular This means that we must have m T cdot m N 1 Tangent and normal to a curve are perpendicular to each other at the point of contact Learn how to derive the equations of tangents and normals at a given point to a curve along with examples here at BYJU S
gradient of normal and tangent

gradient of normal and tangent
https://i.ytimg.com/vi/xCry_G4-F90/maxresdefault.jpg

Equation Of Tangent And Normal To A Curve With Examples My XXX Hot Girl
http://3.bp.blogspot.com/-f4xWX5o5Tsk/TrsGjNwf_II/AAAAAAAACiA/K3nLYEdFgDc/s1600/Picture5.png
Differentiation Tangents And Normals examples Worksheets Videos
https://www.onlinemathlearning.com/image-files/tangent-normal.png
Tangents and normals are the lines associated with curves The tangent is a line touching the curve at a distinct point and each of the points on the curve has a tangent Normal is a line perpendicular to the tangent at the point of contact When dealing with a function y f x of one variable we stated that a line through c f c was tangent to f if the line had a slope of f c and was normal or perpendicular orthogonal to f if it had a slope of 1 f c We extend the concept of normal or orthogonal to functions of two variables
This unit explains how di erentiation can be used to calculate the equations of the tangent and normal to a curve The tangent is a straight line which just touches the curve at a given point The normal is a straight line which is perpendicular to the tangent In this section discuss how the gradient vector can be used to find tangent planes to a much more general function than in the previous section We will also define the normal line and discuss how the gradient vector can
More picture related to gradient of normal and tangent

4 1 GRADIENT TANGENT AND NORMAL TO A CURVE PART 2 YouTube
https://i.ytimg.com/vi/ZdONyyD-Fqg/maxresdefault.jpg
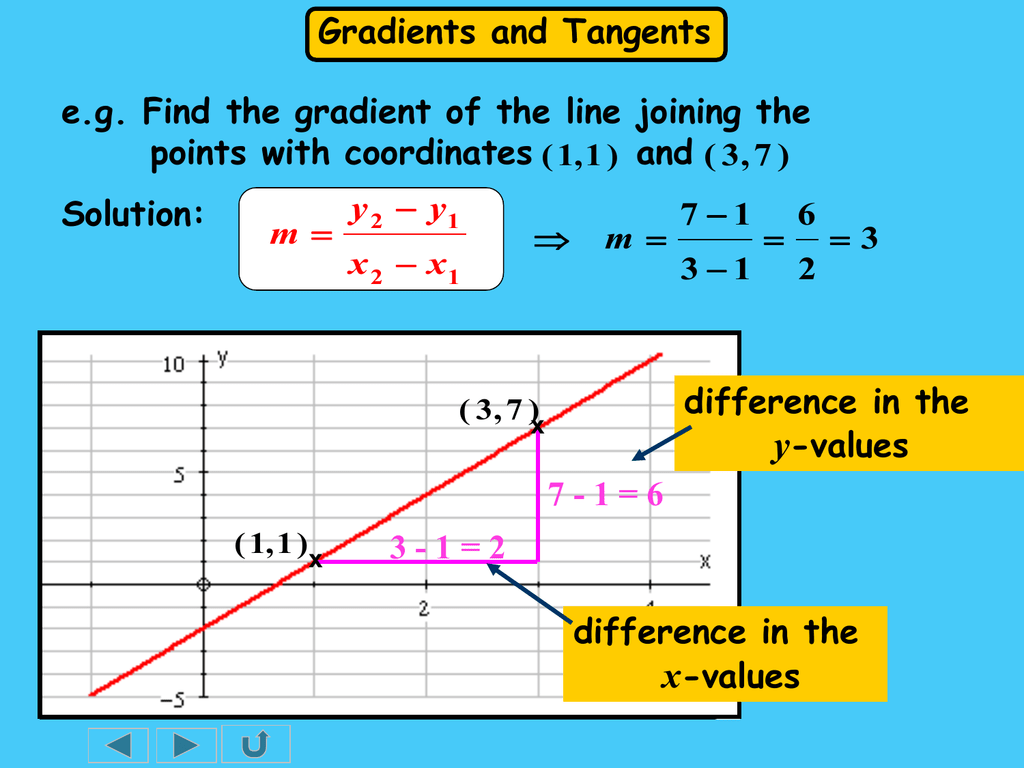
Tangents And Gradients
https://s2.studylib.net/store/data/005729350_1-0b04623678bd976495054fa381567cd3.png

Tangents And Normals Introduction Definition Videos Solved Examples
https://d1whtlypfis84e.cloudfront.net/guides/wp-content/uploads/2018/04/02174230/800px-Tangent.png
Normal Lines Given a vector and a point there is a unique line parallel to that vector that passes through the point In the context of surfaces we have the gradient vector of the surface at a given point This leads to the following definition Use the gradient to find the tangent to a level curve of a given function The right hand side of the Directional Derivative of a Function of Two Variables is equal to fx x y cos fy x y sin which can be written as the dot product of two vectors
[desc-10] [desc-11]

Gradient Of A Tangent YouTube
https://i.ytimg.com/vi/jUEANGqkqZc/maxresdefault.jpg

Equations Of Tangents
https://image.slidesharecdn.com/equations-of-tangents-160217234536/95/equations-of-tangents-4-638.jpg?cb=1455752771
gradient of normal and tangent - [desc-12]