expand using binomial theorem x 2y 6 Expand binomials using the binomial expansion method step by step binomial expansion calculator en Related Symbolab blog posts Middle School Math Solutions Expand Calculator Distributive Law The distributive law helps with multiplication problems by breaking down large numbers into smaller numbers In
How to expand x 2 2y 6 using the binomial theorem Socratic Precalculus 1 Answer Chirag Mehta Jan 16 2018 See a solution process below Explanation Here xnCr n r n r Similarly you can do for any value of n and r except the negative ones you will require to first make n power to which it is raised positive Expand the Trigonometric Expression x 2y 6 x 2y 6 x 2 y 6 Use the Binomial Theorem x6 6x5 2y 15x4 2y 2 20x3 2y 3 15x2 2y 4 6x 2y 5 2y 6 x 6 6 x 5 2 y 15 x 4 2 y 2 20 x 3 2 y 3 15 x 2 2 y 4 6 x 2 y 5 2 y 6 Simplify each term Tap for more steps
expand using binomial theorem x 2y 6
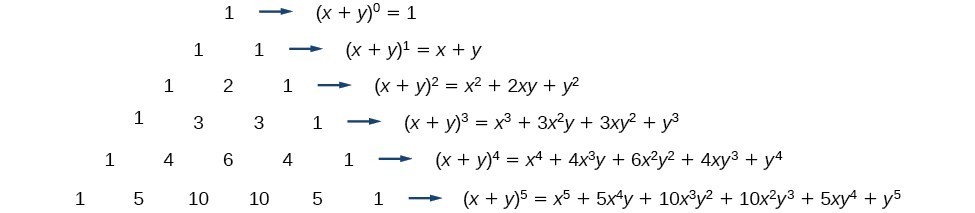
expand using binomial theorem x 2y 6
https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/896/2016/11/03234328/CNX_Precalc_Figure_11_06_0032.jpg

23 The Binomial Theorem Binomial Expansion Part 1 YouTube
https://i.ytimg.com/vi/SwaVN0epc0w/maxresdefault.jpg

Question Video Finding The Coefficient Of A Certain Term In A Binomial
https://media.nagwa.com/254128151254/en/thumbnail_l.jpeg
A closer look at the Binomial Theorem The easiest way to understand the binomial theorem is to first just look at the pattern of polynomial expansions below x y 2 x 2 2xy y 2 x y 3 x 3 3x 2 y 3xy 2 y 3 x y Expand Using the Binomial Theorem x 2 y 2 6 x2 y2 6 x 2 y 2 6 Use the binomial expansion theorem to find each term The binomial theorem states a b n n k 0nCk an kbk a b n k 0 n n C k a n k b k 6 k 0 6 6 k k x2 6 k y2 k k 0 6 6 6 k k x 2 6 k y 2 k Expand the summation
Using the Binomial Theorem to Find a Single Term Expanding a binomial with a high exponent such as x 2y 16 can be a lengthy process Sometimes we are interested only in a certain term of a binomial expansion We do not need to fully expand a binomial to find a single specific term The general term in the expansion of x a n using the binomial theorem formula is T r 1 n C r x n r y r Here r 6 n 10 a 2 Thus by substituting we get T 7 T 6 1 10 C 6 x 10 6 2 6 T 7 210 x 4 64 13440 x 4 Answer 7 th term in x 2 10 is 13440 x 4
More picture related to expand using binomial theorem x 2y 6

9 5 The Binomial Theorem
https://s2.studylib.net/store/data/005635447_1-2b706ccbf50fc2baaa042548c0fc2d32.png

Question Video Using The Binomial Theorem Nagwa
https://media.nagwa.com/964181707396/en/thumbnail_l.jpeg
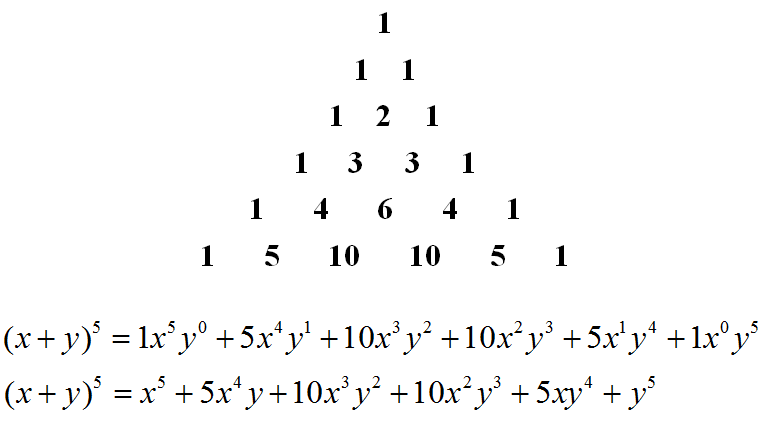
The Binomial Theorem
http://ww.statisticslectures.com/images/pascal5.gif
Expand the expression x 2 2y 3 5 2xy 2 frac 4 y 2 3 sqrt 2 1 6 i 3 4 Solution We use the binomial theorem with a x 2 and b 2y 3 1 Answer Use Pascal s triangle and choose the row that starts with 1 6 that is 1 6 15 20 15 6 1 Write out the powers of 2 up to 26 as a sequence 1 2 4 8 16 32 64 Multiply the two sequences together 1 12 60 320 480 192 64 Alternate the signs 1 12 60 320 480 192 64
Key Points According to the theorem it is possible to expand the power x y n x y n into a sum involving terms of the form ax by c axbyc where the exponents b b and c c are nonnegative integers with b c n b c n and the coefficient a a of each term is a specific positive integer depending on n n and b b The first term in the binomial is x 2 the second term in 3 and the power n for this expansion is 6 So counting from 0 to 6 the Binomial Theorem gives me these seven terms x 2 3 6 6 C 0 x 2 6 3 0

What Is The Coefficient Of The Third Term In A Binomial That Is Raised
https://mathsathome.com/wp-content/uploads/2021/10/list-of-binomial-expansion-formulae-1024x579.png

How To Do The Binomial Expansion Mathsathome
https://mathsathome.com/wp-content/uploads/2021/10/binomial-expansion-with-a-negative-1024x578.png
expand using binomial theorem x 2y 6 - 1 Here we show you a step by step solved example of binomial theorem This solution was automatically generated by our smart calculator left x 3 right 5 2 We can expand the expression left x 3 right 5 using Newton s binomial theorem which is a formula that allow us to find the expanded form of a binomial raised to a positive