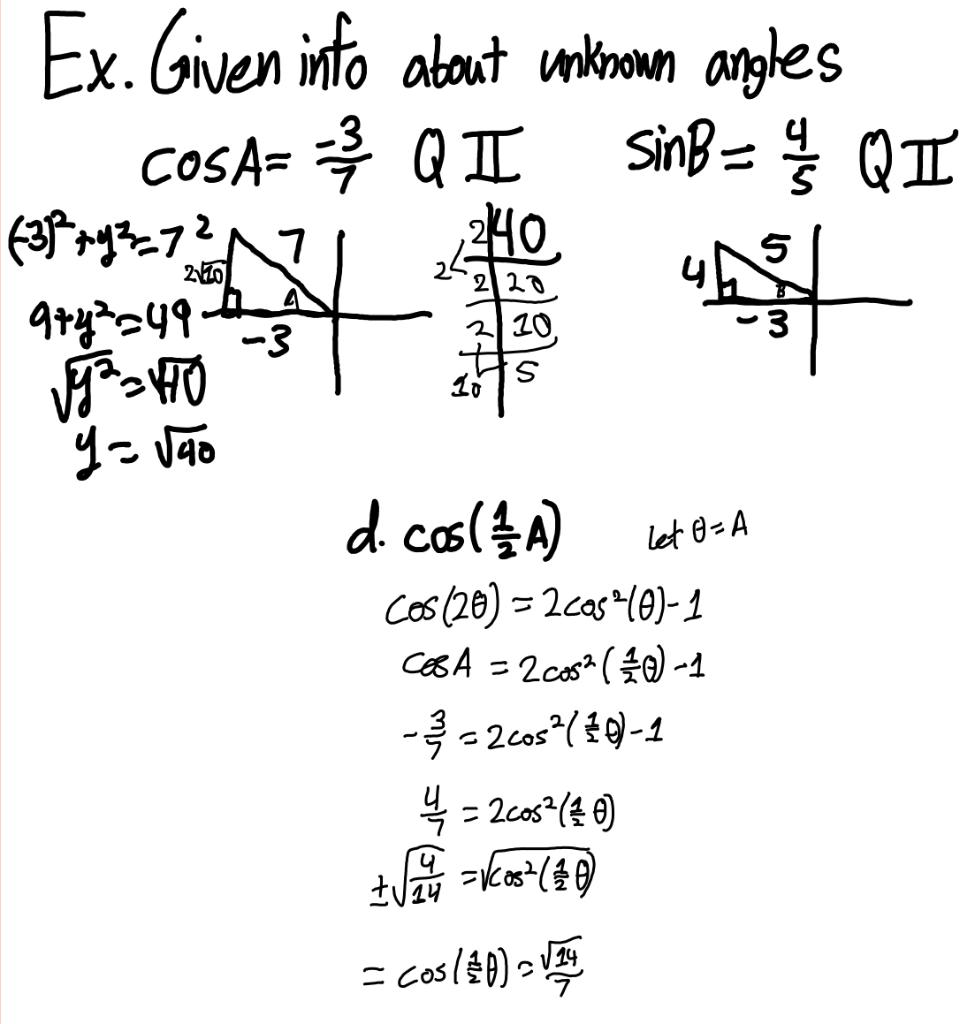double angle identities explained What are Double Angle Identities How do you use a double angle identity to find the exact value of each expression How do you use a double angle identity to find the exact value of sin 120 How do you use double angle identities to solve equations How do you find all solutions for sin2x cosx for the interval 0 2
We can use the double angle identities to simplify expressions and prove identities Example PageIndex 3 Simplify dfrac cos 2t cos t sin t These new identities are called Double Angle Identities prime prime because they typically deal with relationships between trigonometric functions of a particular angle and functions of two times or double the original angle
double angle identities explained
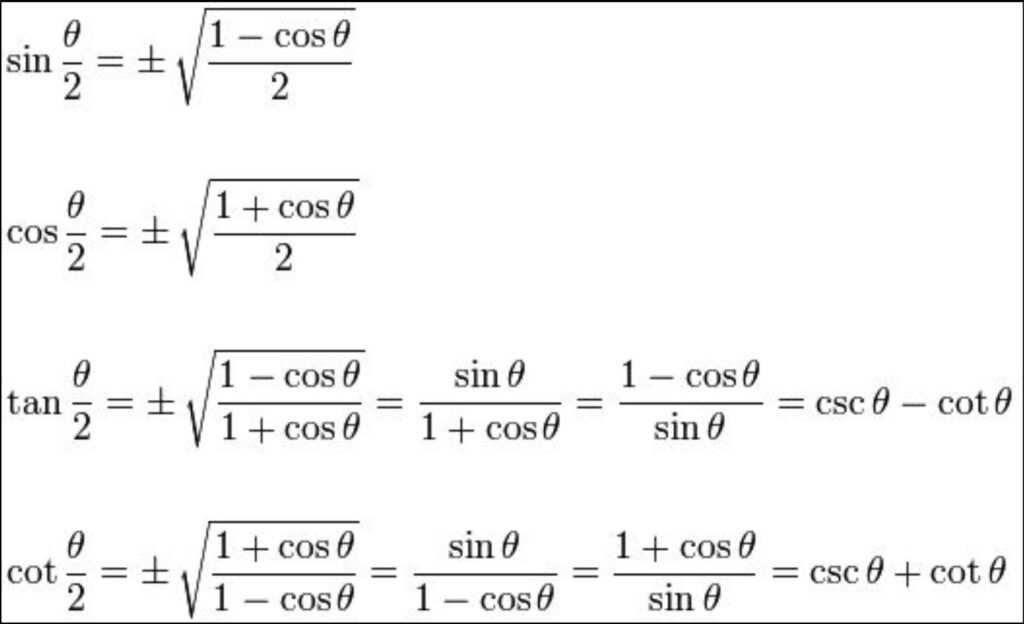
double angle identities explained
https://trigidentities.net/wp-content/uploads/2022/10/Half-Angle-Trig-Identities-1024x624.jpg
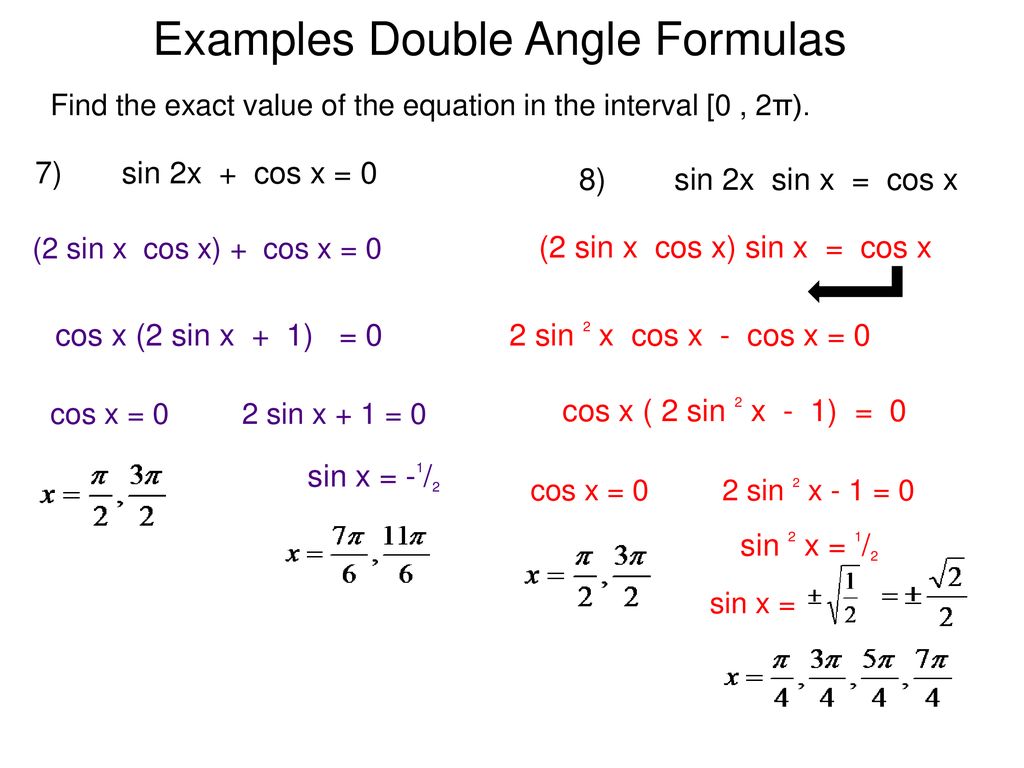
Double Angle Trig Identities With Formulas And Examples
https://trigidentities.net/wp-content/uploads/2023/02/Double-Angle-Trig-Identities-with-Formulas-and-Examples.jpg
Double Angle Identities Worksheet With Graphysc Calculator PDF
https://imgv2-1-f.scribdassets.com/img/document/239122524/original/40f5c63610/1707608731?v=1
Double angle identities are derived from the sum formulas of the fundamental trigonometric functions sine cosine and tangent See Example PageIndex 1 Example PageIndex 2 Example PageIndex 3 and Example PageIndex 4 Double angle identities are trigonometric identities used to rewrite trigonometric functions such as sine cosine and tangent that have a double angle such as 2 These identities are derived using the angle sum identities
Special cases of the sum and difference formulas for sine and cosine yields what is known as the double angle identities and the half angle identities The cosine double angle formula tells us that cos 2 is always equal to cos sin For example cos 60 is equal to cos 30 sin 30 We can use this identity to rewrite expressions or solve problems See some examples in this video
More picture related to double angle identities explained
Math2412 Double Angle Power Reducing Half Angle Identities PDF
https://imgv2-1-f.scribdassets.com/img/document/505329426/original/a7bd729c26/1709188839?v=1

Cofunction Identities Examples Practice Problems Trigonometry YouTube
https://i.ytimg.com/vi/35fxto48HZY/maxresdefault.jpg

Angle
https://cdna.artstation.com/p/assets/images/images/050/252/000/original/-angle.gif?1654432110
Double angle identities can help you find the sine and cosine of a double angle We ll guide you throgh examples then you can try out our practice problems In trigonometry double angle identities relate the values of trigonometric functions of angles that are twice as large as a given angle These identities can be derived from the sum and difference identities for sine and cosine
The double angle identities are trigonometric identities that give the cosine and sine of a double angle in terms of the cosine and sine of a single angle Two additional double angle identities are sometimes given that combine the pythagorean identity and Double angle formulas are used to express the trigonometric ratios of double angles 2 in terms of trigonometric ratios of angle Understand the double angle formulas with derivation examples and FAQs

Double Angle Identities Example 4 Numerade
https://cdn.numerade.com/coursevideos_previews/PRECALC_HALF-ANGLE-IDENTITIES_large.jpg
Solved Explain The Solution Only Using The Double Angle Chegg
https://media.cheggcdn.com/media/035/03583254-74b1-4921-8a47-3e39f764bcce/phpTDyAFr
double angle identities explained - Special cases of the sum and difference formulas for sine and cosine yields what is known as the double angle identities and the half angle identities