cosine limit identity There are six trigonometric functions and the limit of each of these functions leading to the point However we can calculate the limits of these functions according to the continuity of the function considering the domain and range of trigonometric functions
Limits Involving Trigonometric Functions The trigonometric functions sine and cosine have four important limit properties You can use these properties to evaluate many limit problems involving the six basic trigonometric functions Example 1 Evaluate Substituting 0 for x you find that cos x approaches 1 and sin x 3 approaches 3 hence Proofs of trigonometric identities There are several equivalent ways for defining trigonometric functions and the proofs of the trigonometric identities between them depend on the chosen definition The oldest and most elementary definitions are based on the geometry of right triangles
cosine limit identity

cosine limit identity
https://i.ytimg.com/vi/L0n_0GHd6QQ/maxresdefault.jpg

A Limit Of A Cosine Sum Using Euler s Formula For Sin X x YouTube
https://i.ytimg.com/vi/GF8tQlaOErc/maxresdefault.jpg

Proving A Trigonometric Identity 1 cosx 1 secx sinxtanx YouTube
https://i.ytimg.com/vi/bT6JCaSUnDA/maxresdefault.jpg
In order to evaluate the derivatives of sine and cosine we need to evaluate In order to find these limits we will need the following theorem of geometry If x is the measure of the central angle of a circle of radius r then the area A of the sector determined by x is A r2x 2 Let s start by looking at If 10 1 Limits of the Six Trigonometric Functions We start with the simple limit lim sin x Here x c because c we are taking sin of it And because x the radian measure x approaches c we sin x sin c interpret c as a radian measure too The picture on
Cosine Limit lim x 0 cos x 1 x 0 This identity often used in conjunction with the Sine Limit to evaluate complex limits involving cosine functions Tangent Limit lim x 0 tan x x 1 It a key identity for solving limits involving tangent functions and derived from the Sine and Cosine Limits This video covers limits of trigonometric functions focusing on sine cosine and tangent It emphasizes that sine and cosine are continuous and defined for all real numbers so their limits can be found using direct substitution
More picture related to cosine limit identity

Trigonometric Chart Cuemath
https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/mahima-trig-chart-10-1605865895.png
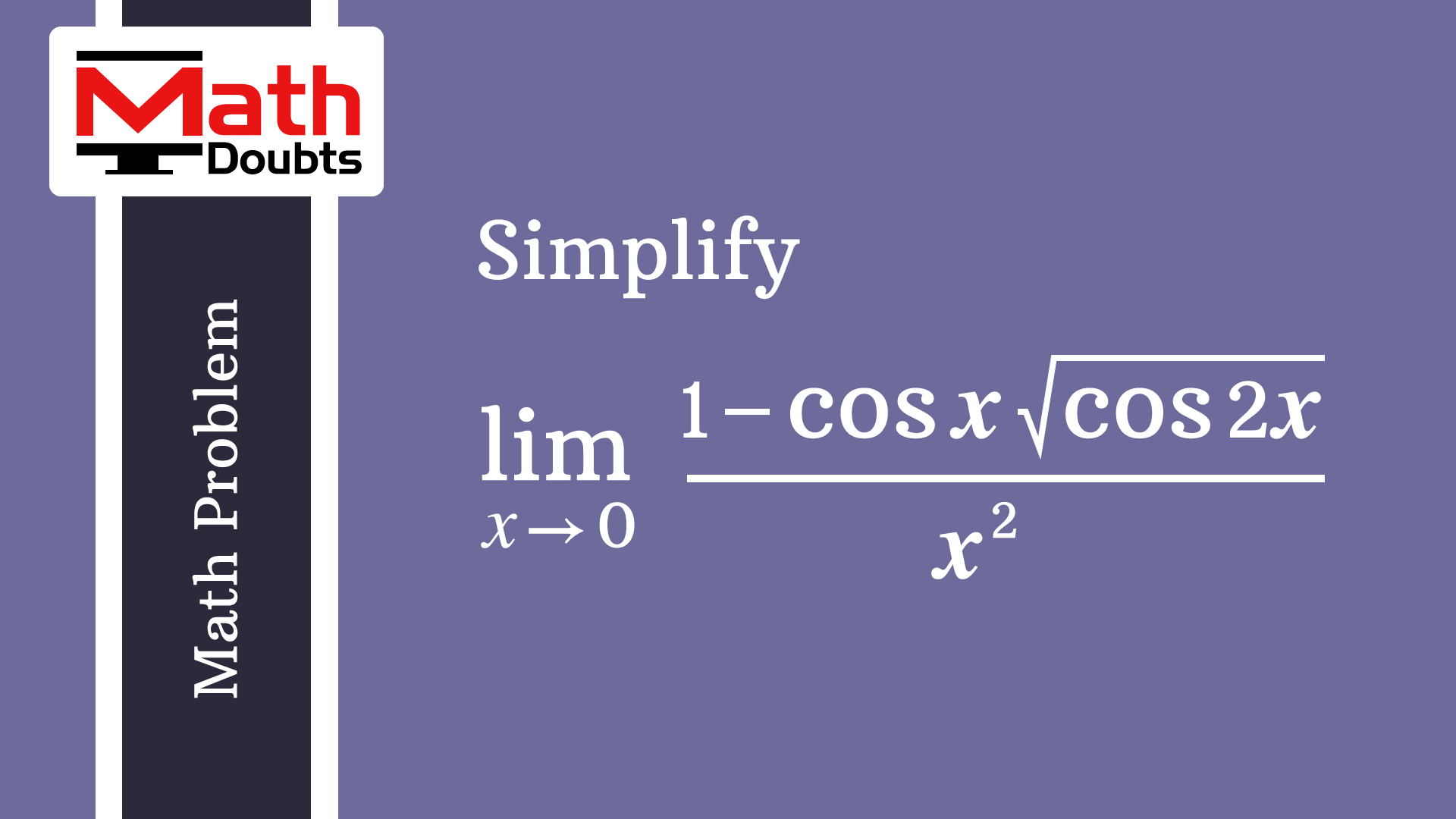
Simplify 1 cosx cos2x x 2 When X Tends To 0
https://farm5.staticflickr.com/4423/36405995915_e98b50ac56_o.jpg
Option 8 Cosine Limit Identity YouTube
https://i.ytimg.com/vi/mVVZW5NP-Q8/maxresdefault.jpg?sqp=-oaymwEmCIAKENAF8quKqQMa8AEB-AH-CYAC0AWKAgwIABABGFUgZChlMA8=&rs=AOn4CLDngoZXdP7I0QUeMKc7tuSI-ZJsuA
Lim x 0 cos x 1 x 0 We determine this by utilising L hospital s Rule Or in words the limit of the quotient of two functions is equal to the limit of the quotient of their derivatives In the example provided we have f x cos x 1 and g x x In this section we give proofs for the two limits that are needed to find the derivative of the sine and cosine functions using the definition of the derivative
[desc-10] [desc-11]

Trigonometric Identities A Plus Topper
https://www.aplustopper.com/wp-content/uploads/2017/04/Trigonometric-Identities-2.jpg

Trigonometry Mathematics Formula
https://d1avenlh0i1xmr.cloudfront.net/d335a910-53a1-41f6-8b2c-3fca79a5db6e/limits-of-trigonometry-functions.jpg
cosine limit identity - This video covers limits of trigonometric functions focusing on sine cosine and tangent It emphasizes that sine and cosine are continuous and defined for all real numbers so their limits can be found using direct substitution